Частота (статистика)

В этой статье объясняется, что такое понятие частоты в статистике. Таким образом, вы найдете определение частоты в статистике, различные существующие типы частот и, наконец, как создать таблицу частот.

Что такое частота в статистике?

В статистике частота — это количество раз, когда значение появляется в наборе данных. Проще говоря, частота — это количество повторений значения в статистической выборке.

Например, если в опросе пять человек ответили, что их любимый цвет — синий, то частота синего цвета равна 5.

Обычно в статистике буква f с индексом i используется для обозначения частоты значения i , поэтому частота обозначается символом _fi .

Сумма всех частот дает общее количество данных в выборке. Следовательно, следующая формула всегда справедлива для любого статистического исследования:

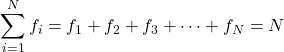
Золото

частота значения

И

общее количество наблюдений.

Виды частот в статистике

В статистике различают следующие типы частот :

• Абсолютная частота : соответствует количеству раз, которое значение появляется в статистической выборке.
• Кумулятивная абсолютная частота : рассчитывается путем сложения абсолютной частоты значения плюс абсолютные частоты всех меньших значений.
• Относительная частота : это абсолютная частота, деленная на общее количество данных.
• Кумулятивная относительная частота : равна сумме относительной частоты значения плюс относительные частоты всех нижних значений.

В разделе ниже вы можете увидеть, как рассчитывается каждый тип частоты.

Таблица частот

Обычно в статистике расчеты частот выборки данных суммируются в таблице частот. Ниже приведен пошаговый пример, чтобы вы могли увидеть, как это сделать.

• Оценки, полученные по предмету «Статистика» в классе из 30 учащихся, следующие. Постройте таблицу частот набора данных.

Поскольку все числа могут быть только целыми числами, это дискретная переменная. Поэтому нет необходимости группировать данные по интервалам.

Поэтому нам нужно построить таблицу, в которой каждое отдельное значение будет строкой. Кроме того, нам нужно найти абсолютную частоту каждого значения, для этого просто подсчитайте, сколько раз значение появляется в выборке данных.

Обратите внимание, что сумма всех абсолютных частот равна общему количеству данных. Если это правило не соблюдается, это означает, что вы забыли предоставить определенную информацию.

Теперь, когда мы знаем абсолютную частоту, нам нужно найти совокупную абсолютную частоту. Для этого расчета у нас есть два варианта: либо мы складываем абсолютную частоту значения плюс все абсолютные частоты наименьших значений, либо, наоборот, складываем абсолютную частоту значения плюс накопленную абсолютную частоту предыдущего значения.

Совокупная абсолютная частота последнего значения всегда соответствует общему количеству данных. Этот трюк можно использовать, чтобы убедиться в правильности расчетов.

Далее нам нужно определить относительную частоту, которая рассчитывается путем деления абсолютной частоты на общее количество точек данных (30):

Имейте в виду, что сумма всех относительных частот всегда равна 1, иначе это означает, что некоторые расчеты в таблице частот неверны.

Наконец, достаточно извлечь накопленную относительную частоту. Для этого необходимо сложить относительную частоту рассматриваемого значения плюс все предыдущие относительные частоты или, что то же самое, предыдущую накопленную относительную частоту:

Вкратце, таблица частот со всеми частотами проблемных данных выглядит следующим образом: