Ранг (статистика)

В этой статье мы объясним, что такое диапазон в статистике и как он рассчитывается. Вы найдете решенное упражнение по объему набора данных, и, наконец, мы покажем вам, для чего он нужен и когда его следует использовать.

Что такое диапазон в статистике?

В статистике диапазон — это мера дисперсии, которая указывает на разницу между максимальным и минимальным значением данных выборки. Следовательно, чтобы рассчитать размер генеральной совокупности или статистической выборки, максимальное значение необходимо вычесть из минимального значения.

Например, если максимальное значение набора данных равно 9, а минимальное значение — 2, диапазон этой статистической выборки равен 7 (9-2=7).

Статистический диапазон также называют протяженностью или диапазоном измерения.

Итак, диапазон — это мера дисперсии с дисперсией, стандартным отклонением (или стандартным отклонением), средним отклонением и коэффициентом вариации.

Как рассчитать диапазон в статистике

Размах выборки рассчитывается путем вычитания крайних значений данных статистической выборки, то есть диапазон выборки равен максимальному значению всех данных минус минимальное значение .

Таким образом, формула для расчета статистического диапазона набора данных выглядит следующим образом:

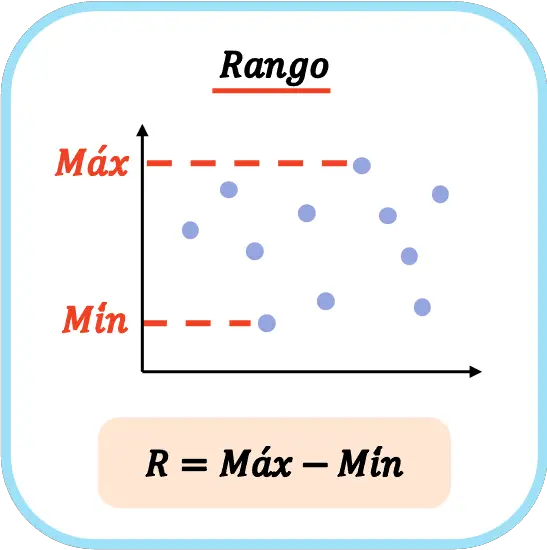
В статистике символ заглавной буквы R часто используется для обозначения размера ряда данных.

Таким образом, вычислить диапазон набора данных довольно просто, поскольку вам просто нужно определить разницу между экстремальными значениями. Единственное, на что вам нужно обратить внимание, это правильно указать максимальные и минимальные данные и не забыть ни одного числа.

Пример диапазона (статистика)

Увидев определение диапазона в статистике, ниже приведен рабочий пример, чтобы вы могли увидеть, как получается диапазон набора данных.

• Компания хочет статистически проанализировать продажи своего флагманского продукта за последние двадцать лет. Для этого они просят вас рассчитать несколько статистических показателей, включая рейтинг. Если продажи продукта показаны в следующей таблице, каков диапазон этого набора данных?

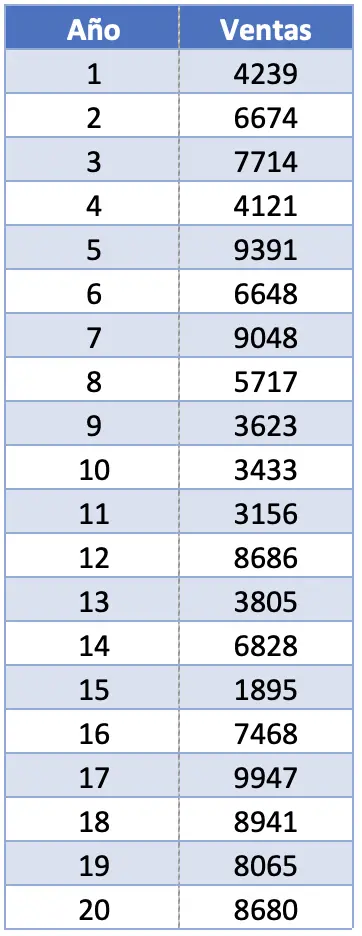
В этом упражнении у нас есть 20 наблюдений. В действительности общее количество наблюдений не имеет значения при расчете размера выборки, поскольку нас интересуют только наибольшее и наименьшее значения.

Поэтому мы должны использовать приведенную выше формулу, чтобы определить объем этой статистической выборки.

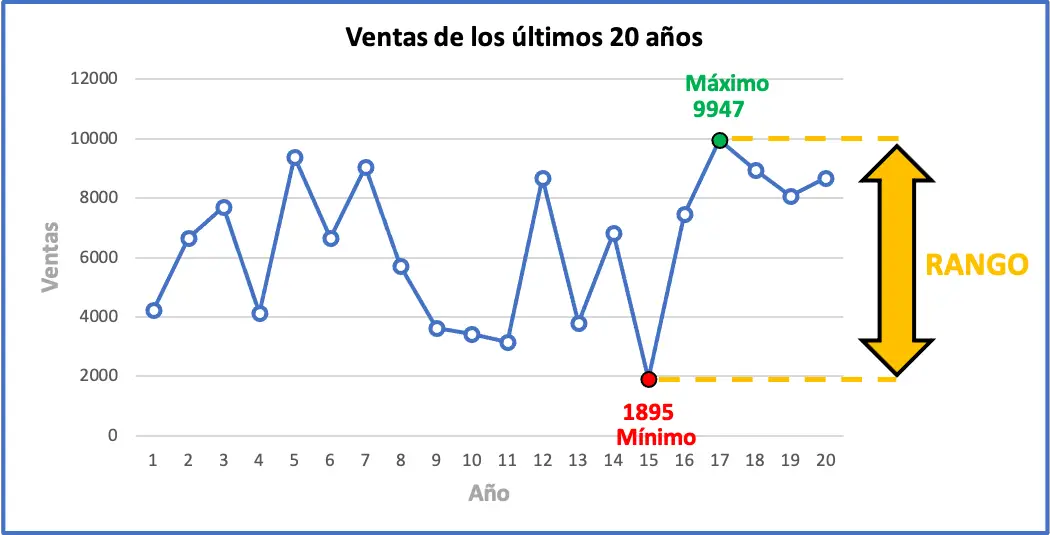
Максимальное значение интервала — 9947 проданных единиц, а минимальное — 1895. Следовательно, нам нужно вычесть эти два значения, чтобы найти диапазон набора данных:

Это означает, что максимальное изменение продаж за последние несколько лет составляет 8052 единицы. Ниже вы можете графически увидеть все данные упражнений вместе с их статистическим диапазоном. Этот график, вероятно, поможет вам понять значение диапазона.

Для чего используется статистический диапазон?

Чтобы завершить понимание понятия масштаба в статистике, мы увидим, для чего оно используется и как интерпретировать эту меру дисперсии.

В статистике диапазон показывает разницу между максимальным и минимальным значением набора данных. Таким образом, диапазон — это мера, которая используется для обозначения общей дисперсии набора данных .

Когда вы знаете значение диапазона набора данных, вы знаете максимальную разницу между любыми двумя наблюдениями в этом наборе, поэтому вы можете получить представление о том, разбросаны ли данные или расположены близко друг к другу. В общем, выгодно, чтобы диапазон был как можно меньшим, потому что это означает, что дисперсия небольшая и, следовательно, расчеты будут более точными.

Например, диапазон может представлять собой измерение, позволяющее сравнивать два разных образца, поскольку оно позволяет получить представление о дисперсиях образцов.

Однако следует проявлять осторожность при интерпретации статистического диапазона, поскольку он может ввести в заблуждение. Возможно, набор данных на самом деле имеет очень низкую дисперсию, но если в выборке есть выброс , диапазон будет очень широким и, следовательно, не будет должным образом отражать дисперсию выборки.

Более того, это не то же самое, что выборка, значения которой имеют порядок десятков, иметь ранг 5, а выборка, значения которой имеют порядок тысяч, иметь тот же ранг. Логично, что даже если оба диапазона имеют одинаковую численность, первая выборка гораздо более дисперсна, чем вторая.

В заключение отметим, что диапазон является полезной статистической мерой для анализа дисперсии набора данных, но для правильной интерпретации данных необходимо рассчитывать и другие показатели.