Мода (статистика)
В этой статье объясняется, что такое режим в статистике. Вы узнаете, как найти статистический режим для сгруппированных и разгруппированных данных, различные типы режима и несколько примеров этого статистического показателя.
Что такое режим в статистике?
В статистике мода — это значение в наборе данных, имеющее наибольшую абсолютную частоту, то есть мода — это наиболее повторяющееся значение в наборе данных.
Поэтому, чтобы вычислить моду набора статистических данных, просто подсчитайте, сколько раз каждый элемент данных появляется в выборке, и наиболее повторяющиеся данные будут модой.
Режим используется для определения статистического распределения, поскольку наиболее повторяющееся значение обычно находится в центре распределения.
Этот режим также можно назвать статистическим режимом или модальным значением . Аналогичным образом, когда данные группируются по интервалам, наиболее повторяющийся интервал — это модальный интервал или модальный класс .
В общем, термин Mo используется как символ статистического режима, например, режим распределения X представляет собой Mo(X).
Имейте в виду, что мода — это статистическая мера положения центра, а также медианы и среднего значения. Ниже мы увидим, что означает каждый из этих статистических показателей.
Типы режимов в статистике
В статистике выделяют несколько типов режимов, которые классифицируются по количеству наиболее повторяющихся значений:
- Унимодальный режим : имеется только одно значение с максимальным количеством повторений. Например, [1, 4, 2, 4, 5, 3].
- Бимодальный режим : максимальное количество повторов происходит при двух разных значениях, и оба значения повторяются одинаковое количество раз. Например, [2, 6, 7, 2, 3, 6, 9].
- Мультимодальный режим : три и более значений имеют одинаковое максимальное количество повторений. Например, [3, 3, 4, 1, 3, 4, 2, 1, 4, 5, 2, 1].
Как найти статистический режим
Чтобы найти статистический режим набора данных, необходимо выполнить следующие шаги:
- Приведите данные в порядок. Этот шаг не является обязательным, но он облегчит подсчет чисел.
- Посчитайте, сколько раз встречается каждое число.
- Число, которое появляется чаще всего, представляет собой статистический режим.
Примеры статистического режима
Рассматривая определение моды в статистике, ниже вы можете увидеть пример каждого вида моды, чтобы вы могли лучше понять концепцию.
Пример унимодального режима
- Каков режим следующего набора данных?
![]()
Числа не упорядочены, поэтому сначала упорядочим их, чтобы было легче найти режим.
![]()
Цифры 2 и 9 встречаются дважды, а цифра 5 повторяется три раза. Следовательно, мода ряда данных имеет номер 5.
![]()
Пример бимодального режима
- Рассчитайте режим следующего набора данных:
![]()
![]()
Сначала расставим цифры по порядку:
![]()
![]()
Как видите, всего цифра 6 и цифра 8 встречаются четыре раза, что является максимальным количеством повторений. Следовательно, в данном случае это бимодальный режим, а два числа — это режим набора данных:
![]()
Пример мультимодального режима
- Найдите следующий режим набора данных:
![]()
![]()
![]()
Поскольку данных много, сначала сортируем их по возрастанию, чтобы было легче считать:
![]()
![]()
![]()
Наиболее повторяющиеся числа — 20, 27 и 31, все три числа повторяются пять раз. Таким образом, режим этого примера является мультимодальным.
![]()
модный калькулятор
Введите данные из любой статистической выборки в следующий онлайн-калькулятор, чтобы рассчитать ее режим. Данные должны быть разделены пробелом и введены с использованием точки в качестве десятичного разделителя.
Режим для сгруппированных данных
Когда у нас есть данные, сгруппированные в виде интервалов, мы на самом деле не знаем, сколько раз повторяется каждый фрагмент данных, мы знаем только частоту каждого интервала.
Таким образом, для расчета режима данных, сгруппированных по интервалам, мы должны использовать следующую формулу :
![]()
Золото:
- L i – нижняя граница модального интервала (наивысший абсолютный частотный интервал).
- f i — абсолютная частота модального интервала.
- f i-1 — абсолютная частота интервала перед модальным.
- f i+1 — абсолютная частота интервала после модального.
- A i – ширина модального интервала.
В качестве примера ниже вы решили упражнение, в котором рассчитывается режим данных, сгруппированных по интервалам:
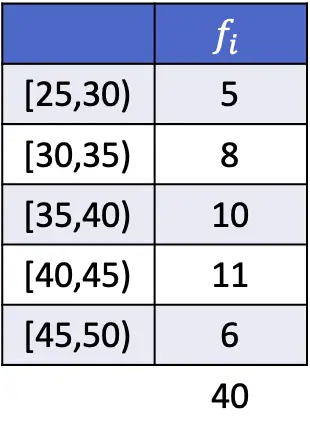
В данном случае модальный интервал равен [40,45), поскольку это интервал с наибольшей абсолютной частотой. Таким образом, параметры формулы режима для сгруппированных данных:
![Rendered by QuickLaTeX.com \begin{array}{c}L_i=40\\[2ex]f_i=11\\[2ex]f_{i-1}=10\\[2ex]f_{i+1}=6\\[2ex]A_i=5\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-85aef7092d3e0c7769ad17b96aae294c_l3.png)
Поэтому мы применяем формулу для определения режима данных, сгруппированных по интервалам, и выполняем расчет:
![Rendered by QuickLaTeX.com \begin{aligned}Mo & =L_i+ \cfrac{f_i-f_{i-1}}{(f_i-f_{i-1})+(f_i-f_{i+1})}\cdot A_i\\[2ex]& =40+ \cfrac{11-10}{(11-10)+(11-6)}\cdot 5\\[2ex]&=40,83\end{aligned}](https://statorials.org/wp-content/ql-cache/quicklatex.com-3ee33fdb43267fdcfc6d222ed6798fca_l3.png)
Разница между модой, средним значением и медианой
В этом последнем разделе мы увидим, в чем разница между модой, средним значением и медианой. Поскольку все три являются статистическими мерами центрального положения, их значение различно.
Как поясняется в статье, мода в математике — это наиболее повторяющееся значение в наборе данных.
Во-вторых, среднее значение — это среднее значение всех статистических данных. Таким образом, чтобы получить среднее значение определенных данных, необходимо сложить все данные, а затем разделить результат на количество наблюдений.
И, наконец, медиана — это значение, занимающее центральное положение при упорядочении данных.
Таким образом, три статистических показателя помогают определить распределение вероятностей, поскольку дают представление о его центральных значениях. Но имейте в виду, что не существует одной меры, которая была бы лучше другой, они просто означают разные концепции.
Модная недвижимость
Свойства моды:
- Мода может быть найдена как в количественных, так и в качественных переменных.
- Если мы применим линейное преобразование к случайной величине, значение среднего будет меняться в зависимости от примененных операций.
- В целом режим нечувствителен к выбросам.
- Если все значения имеют одинаковую частоту, режима нет.
![]()