Стратифицированная выборка

В этой статье мы объясним, что такое стратифицированная выборка и как она проводится. Здесь вы найдете объяснение подтипов стратифицированной выборки и, наконец, каковы преимущества и недостатки стратифицированной выборки.

Что такое стратифицированная выборка?

Стратифицированная выборка — это статистический метод, используемый для отбора элементов выборки путем разделения генеральной совокупности на группы (называемые стратами). То есть при стратифицированной выборке совокупность делится на слои, и лица из каждой страты случайным образом отбираются для формирования всей исследуемой выборки.

Страты — это однородные группы, или, другими словами, индивиды в страте обладают своими характеристиками, отличающими их от других стратов. Таким образом, человек может принадлежать только к одному слою.

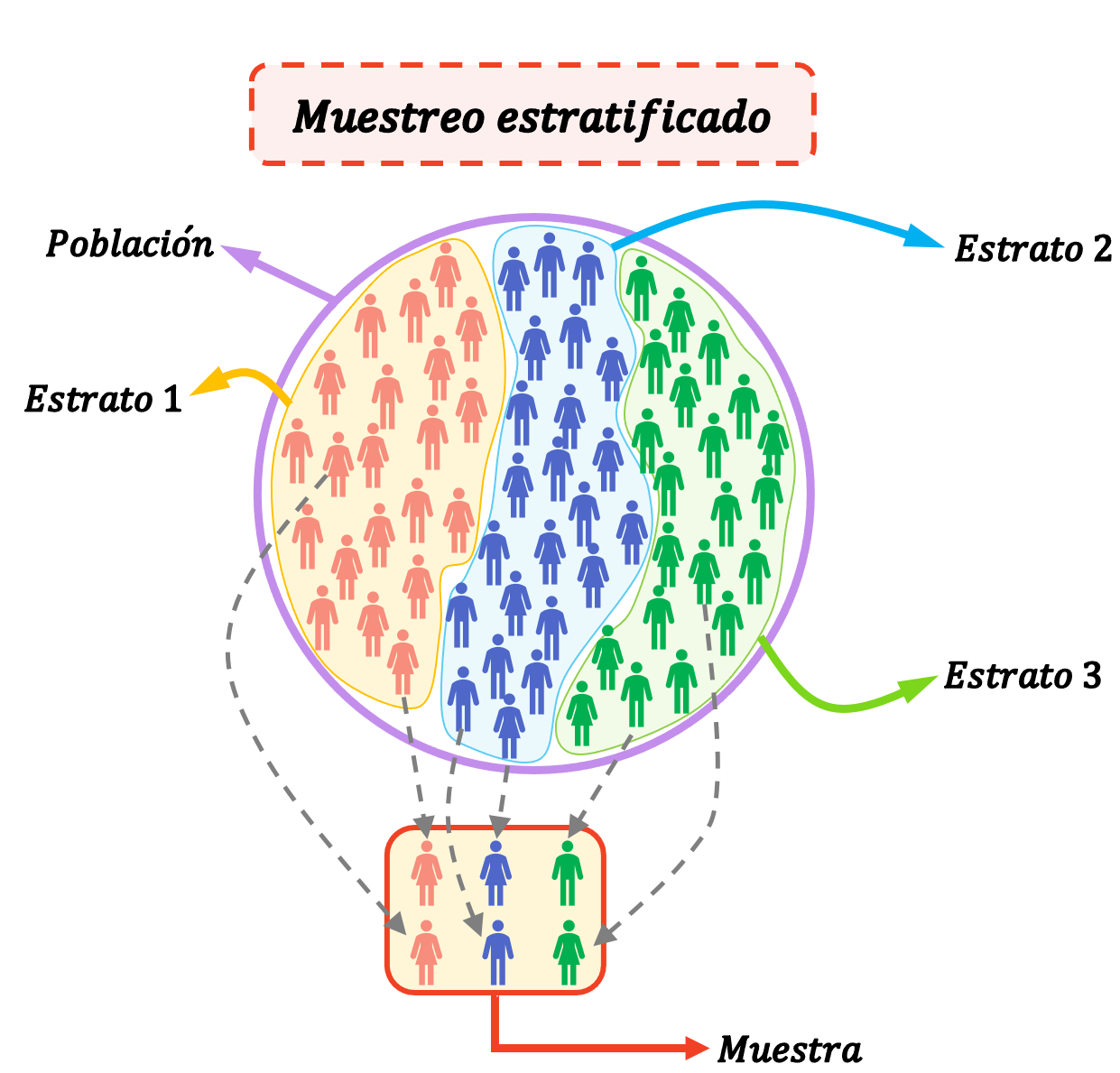
Стратифицированная выборка очень полезна, когда совокупность состоит из очень однородных групп, сильно отличающихся друг от друга.

Логично, что сумма размеров всех слоев дает размер статистической совокупности:

Аналогично, сумма размера выборки, выбранной в каждой страте, равна общему размеру выборки статистического исследования:

Обычно мы различаем прописные и строчные буквы для обозначения генеральной совокупности или выборки соответственно.

Как сделать стратифицированную выборку

Этапы проведения стратифицированной выборки следующие:

1. Определите целевую группу населения.
2. Выберите переменную стратификацию и количество страт.
3. Определите , к какому слою принадлежит каждый элемент совокупности.
4. Рассчитайте размер каждой страты , которая будет частью выборки.
5. Случайным образом выберите элементы из каждой страты , которые будут принадлежать исследуемой выборке. Для каждой страты необходимо выбрать столько элементов, сколько было решено на предыдущем этапе.

Имейте в виду, что размер каждой страты в выборке зависит не только от размера страты, но и от типа стратифицированной выборки. Далее на примере объясняется каждый тип стратифицированной выборки и порядок расчета размера выборки каждой страты.

Типы стратифицированной выборки

Теперь, когда вы знаете определение стратифицированной выборки, вы должны знать, что существует несколько типов стратифицированной выборки, которые классифицируются следующим образом:

• Пропорциональная стратифицированная выборка
• Равномерная стратифицированная выборка
• Выборка оптимальна

Каждый тип стратифицированной выборки подробно объясняется ниже, чтобы лучше понять значение каждого из них.

Пропорциональная стратифицированная выборка

При стратифицированной пропорциональной выборке или выборке с пропорциональным распределением количество элементов из каждой страты, входящих в исследуемую выборку, пропорционально размеру каждой страты.

Таким образом, если один слой больше другого, окончательная выборка будет содержать больше элементов из этого слоя. С другой стороны, если одна страта меньше другой, в выборке статистического анализа будет меньше элементов из этой страты.

Этот тип стратифицированной выборки полезен, когда слои имеют разные размеры и мы хотим, чтобы выборка включала больше элементов из более крупных слоев.

Чтобы вычислить количество элементов из каждой страты , которые будут в выборке, размер каждой страты необходимо разделить на сумму размеров всех страт. Результатом будет доля страты, которая должна быть включена в выборку, поэтому ее необходимо будет умножить на желаемый размер выборки.

Золото

желаемый общий размер выборки,

количество элементов в страте

для включения в выборку,

размер страты

, И

общее количество элементов в популяции.

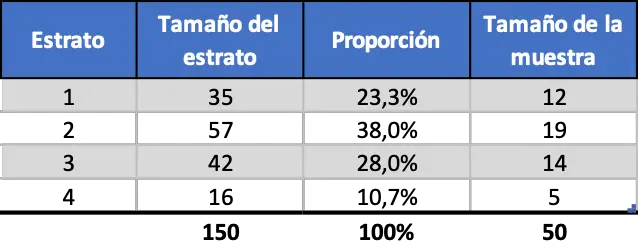
Например, представьте, что мы хотим провести исследование в компании со 150 работниками, взяв выборку из 50 человек и стратифицировав данные по возрасту работников. Мы можем классифицировать данные следующим образом:

• От 20 до 29 лет: 35 работников.
• От 30 до 39 лет: 57 сотрудников.
• От 40 до 49 лет: 42 сотрудника.
• От 50 до 59 лет: 16 сотрудников.

Таким образом, если мы стратифицируем данные пропорционально, выборка будет следующей:

Равномерная стратифицированная выборка

При единой стратифицированной выборке или единой аффиксационной выборке количество элементов из каждой страты, входящих в исследуемую выборку, одинаково.

Таким образом, каждая страта имеет одинаковый вес в этом типе выборки. Независимо от того, содержит ли страта больше или меньше особей, чем другая страта, все они будут представлены в выборке одинаковым количеством индивидов.

В этом случае для расчета размера элементов в каждой страте желаемый размер выборки необходимо разделить на количество существующих страт. Другими словами, следует использовать следующую формулу:

Золото

желаемый общий размер выборки,

количество элементов в страте

кто будет включен в выборку, и

количество слоев, на которые разделено население.

Следуя предыдущему примеру, поскольку мы хотели получить выборку из 50 работников, а всего было 4 разных слоя, размер выборки каждого слоя будет:

Результат представляет собой десятичное число: в некоторых слоях будет 12 рабочих, а в других — 13, пока количество рабочих не достигнет 50. Таким образом, равномерная стратифицированная выборка выглядит следующим образом:

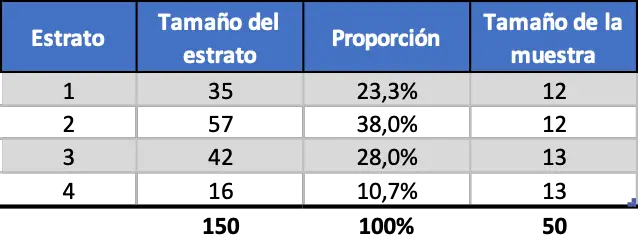
Как видите, размер выборки каждой страты не зависит от доли каждой из них.

Оптимальная стратифицированная выборка

При оптимальной стратифицированной выборке количество элементов в каждой страте пропорционально зависит от изменчивости каждой страты.

Таким образом, слои с большей изменчивостью будут иметь больший размер выборки, и наоборот, слои с меньшей изменчивостью будут иметь меньший размер выборки.

Формула для определения того, сколько элементов из каждой страты войдет в выборку статистического исследования, выглядит следующим образом:

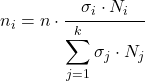
Золото

желаемый общий размер выборки,

количество элементов в страте

для включения в выборку,

это стандартное отклонение (или типичное отклонение) страты

, И

размер слоя

.

Преимущества и недостатки стратифицированной выборки

Стратифицированная выборка имеет следующие преимущества и недостатки:

преимущество	Недостатки
Это дает возможность статистически изучать не только все население, но и каждую отдельную его прослойку.	Это сложный в реализации метод выборки.
Ошибка выборки, допускаемая стратифицированной выборкой, всегда равна или меньше ошибки простой случайной выборки.	Это трудоемкий и, следовательно, дорогостоящий процесс отбора проб.
Это позволяет воспользоваться знаниями исследователя о популяции.	Об анализируемом образце необходимо много информации, чтобы иметь возможность его стратифицировать.
При стратифицированной выборке мы гарантируем, что в выборку будет включен хотя бы один элемент из каждой страты.	Для проведения выборки необходимо знать долю каждой страты.

Основная характеристика стратифицированной выборки заключается в том, что она используется для статистического анализа каждой группы или слоя, на которые была разделена совокупность. Конечно, с помощью такого типа выборки можно изучить и всю популяцию. Кроме того, преимущества стратификации данных будут больше, если слои отличаются друг от друга.

Напротив, факт стратификации данных для проведения выборки подразумевает увеличение сложности выборки, причем стратифицированную выборку сложнее проводить по сравнению с другими типами выборки. Это свойство также означает, что изготовление такой выборки обходится дорого, поскольку для правильного проведения стратификации требуется время.

Еще одним недостатком стратифицированной выборки является то, что она требует большого количества информации о совокупности, которую необходимо изучить, что не требуется при других типах выборки, таких как простая случайная выборка. Хотя этот недостаток можно смягчить, если исследователь обладает глубокими знаниями в этой области.

Наконец, с помощью стратифицированной выборки мы получаем выборку, которая более репрезентативна для генеральной совокупности, чем при других типах выборки, поскольку мы гарантируем, что в нее включены элементы из каждой страты. Напротив, в других выборках полученная выборка может не содержать элементов ни из одной страты.