Теорема чебышева

В этой статье объясняется, что такое теорема Чебышева. Здесь вы найдете формулу теоремы Чебышева, решение упражнения и, кроме того, онлайн-калькулятор теоремы Чебышева. Наконец, показано различие между теоремой Чебышева и эмпирическим правилом.

Что такое Теорема Чебышева?

Теорема Чебышева , также известная как неравенство Чебышева , представляет собой статистическое правило, используемое для расчета вероятности того, что значение случайной величины находится на определенном расстоянии от ее среднего значения.

Другими словами, в статистике теорема Чебышева используется для определения вероятности того, что значение находится в пределах доверительного интервала.

Кроме того, теорема Чебышева также используется для доказательства других статистических теорем, таких как закон больших чисел.

Хотя теорема Чебышева была впервые сформулирована французом Ирене-Жюлем Бьенеме, теорема названа так потому, что ее придумал русский Пафнутий Чебушев в 1867 году.

Формула теоремы Чебышева

Теорема Чебышева гласит, что вероятность того, что значение будет равно k стандартным отклонениям от среднего значения, больше или равна единице минус отношение единицы к k в квадрате.

Следовательно, формула теоремы Чебышева имеет следующий вид:

Золото

— значение случайной величины,

среднее арифметическое переменной,

его стандартное отклонение и

количество стандартных отклонений от среднего значения, по которому рассчитывается вероятность.

Обратите внимание, что эту формулу можно использовать только в том случае, если количество стандартных отклонений, по которым проводится расчет, больше 1, или, другими словами, если k больше 1.

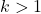Для расчета вероятности вы можете воспользоваться онлайн-калькулятором теоремы Чебышева, расположенным ниже.

Пример теоремы Чебышева

Как только мы увидели определение теоремы Чебышева и ее формулу, вот решенный пример этой статистической теоремы, чтобы лучше понять эту концепцию.

• Если оценки, полученные по статистике университетских курсов, определяются распределением со средним значением 65 и стандартным отклонением 10, какой процент студентов получил оценку от 50 до 80?

Для решения этой задачи нам необходимо применить формулу теоремы Чебышева. Однако сначала мы должны определить, сколько стандартных отклонений составляют значения 50 и 80 от среднего значения переменной, для этого нам просто нужно выполнить следующий расчет:

Следовательно, значения 50 и 80 соответствуют 1,5 стандартным отклонениям от нижнего и верхнего среднего соответственно. Поэтому воспользуемся формулой теоремы Чебышевой при k=1,5:

Таким образом, по крайней мере 55,56% учащихся получили оценку от 50 до 80.

Калькулятор теоремы Чебышева

Введите количество стандартных отклонений между рассматриваемыми значениями и средним значением (k) , затем нажмите «Рассчитать». Затем калькулятор вернет минимальную вероятность доверительного интервала.

Вы должны ввести количество стандартных отклонений, используя точку в качестве десятичного разделителя.

Теорема Чебышева и эмпирическое правило

Двумя тесно связанными понятиями в статистике являются теорема Чебышева и эмпирическое правило, поскольку оба используются для расчета вероятности доверительных интервалов.

Разница между теоремой Чебышева и эмпирическим правилом заключается в том, что теорему Чебышева можно использовать для любого типа распределения, тогда как эмпирическое правило справедливо только для нормального распределения.

Таким образом, использование теоремы Чебышева шире, но эмпирическое правило дает более точные результаты для нормального распределения.

Нажмите здесь, чтобы узнать, в чем именно состоит практическое правило: