Как выполнить тест бреуша-пагана в stata

Множественная линейная регрессия — это метод, который мы можем использовать, чтобы понять взаимосвязь между несколькими объясняющими переменными и переменной отклика.

К сожалению, проблема, которая часто возникает в регрессии, известна как гетероскедастичность , при которой происходит систематическое изменение дисперсии остатков в диапазоне измеренных значений.

Одним из тестов, который мы можем использовать для определения наличия гетероскедастичности, является тест Бреуша-Пэгана . Этот тест дает статистику критерия Хи-квадрат и соответствующее значение p.

Если значение p ниже определенного порога (обычно выбирают 0,01, 0,05 и 0,10), то имеется достаточно доказательств, чтобы сказать, что гетероскедастичность присутствует.

В этом руководстве объясняется, как выполнить тест Бреуша-Пэгана в Stata.

Пример: тест Бреуша-Пагана в Stata

Мы будем использовать автоматически интегрированный набор данных Stata, чтобы проиллюстрировать, как выполнить тест Бреуша-Пэгана.

Шаг 1: Загрузите и отобразите данные.

Сначала используйте следующую команду для загрузки данных:

автоматическое использование системы

Затем отобразите необработанные данные с помощью следующей команды:

бр

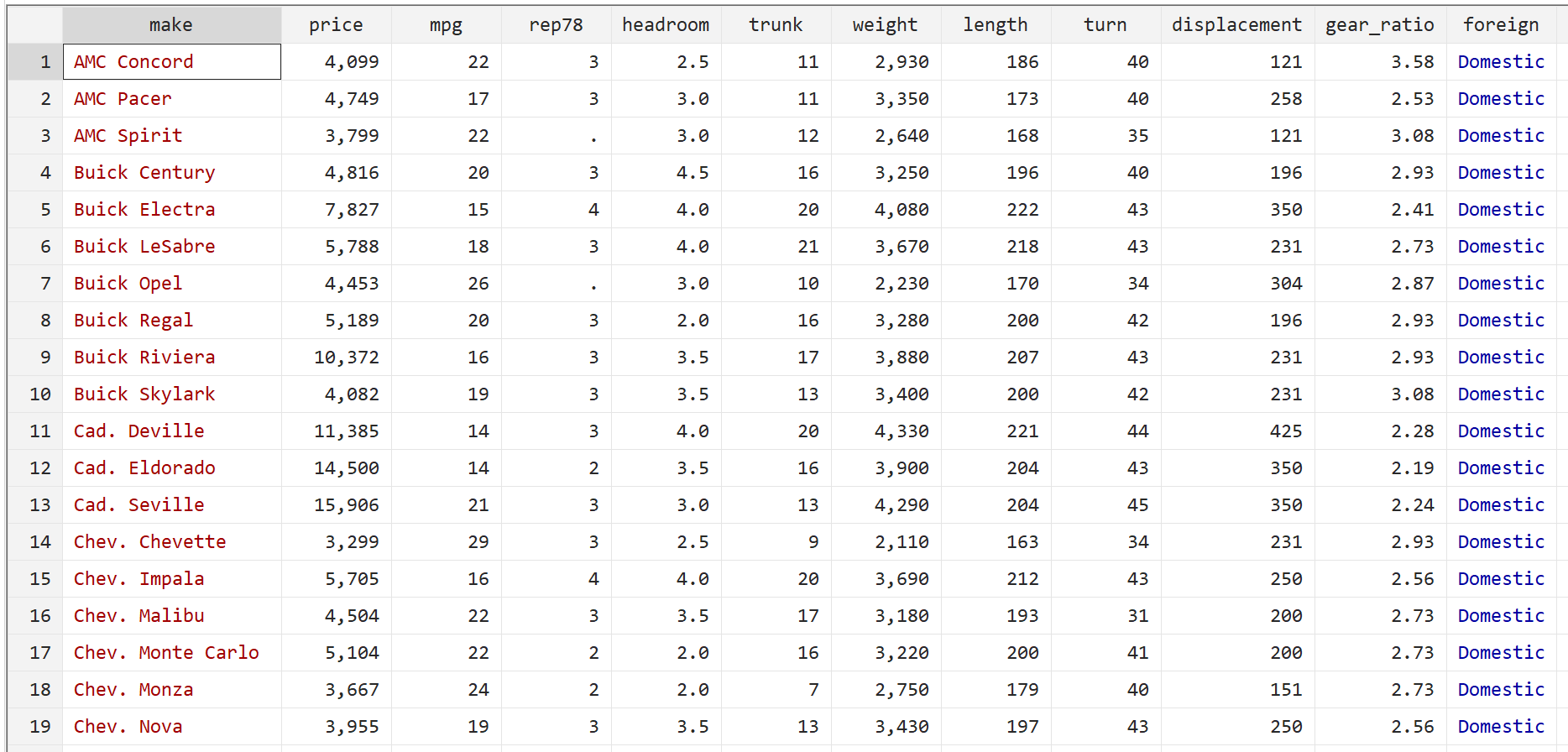
Шаг 2. Выполните множественную линейную регрессию.

Далее мы введем следующую команду, чтобы выполнить множественную линейную регрессию, используя цену в качестве переменной ответа, а миль на галлон и вес в качестве объясняющих переменных:

регрессионная цена, вес миль на галлон

Шаг 3: Выполните тест Бреуша-Пэгана.

После того, как мы подогнали регрессионную модель, мы можем выполнить тест Бреуша-Пэгана, используя команду hettest , что является сокращением от «тест на гетероскедастичность»:

Самый горячий

Вот как интерпретировать результат:

Хо: Это нулевая гипотеза теста, которая утверждает, что между остатками существует постоянная дисперсия.

Переменные: это сообщает нам переменную ответа, которая использовалась в регрессионной модели. В данном случае это была переменная цена .

chi2(1): это статистика теста хи-квадрат. В данном случае это 14:78.

Вероятность > хи2: это значение p, соответствующее статистике теста хи-квадрат. В данном случае это 0,0001. Поскольку это значение меньше 0,05, мы можем отвергнуть нулевую гипотезу и сделать вывод о гетероскедастичности данных.

Что делать дальше

Если вам не удастся отвергнуть нулевую гипотезу теста Бреуша-Пэгана, то гетероскедастичности нет и вы можете приступить к интерпретации результата исходной регрессии.

Однако если отвергнуть нулевую гипотезу теста Бреуша-Пэгана, это означает, что в данных присутствует гетероскедастичность. В этом случае стандартные ошибки, отображаемые в выходной таблице регрессии, являются ненадежными. Существует несколько способов решения этой проблемы, в том числе:

1. Преобразуйте переменную ответа. Вы можете попытаться выполнить преобразование переменной ответа. Например, вы можете использовать log(price) вместо цены в качестве переменной ответа. Как правило, логарифм переменной отклика является эффективным способом устранения гетероскедастичности. Другое распространенное преобразование — использование квадратного корня из переменной ответа.

2. Используйте взвешенную регрессию. Этот тип регрессии присваивает вес каждой точке данных на основе дисперсии ее подобранного значения. По сути, это придает низкий вес точкам данных с более высокими дисперсиями, уменьшая их остаточные квадраты. Использование соответствующих весов позволяет устранить проблему гетероскедастичности.

3. Используйте надежные стандартные ошибки. Устойчивые стандартные ошибки более «устойчивы» к проблеме гетероскедастичности и имеют тенденцию обеспечивать более точную меру истинной стандартной ошибки коэффициента регрессии. Ознакомьтесь с этим руководством , чтобы узнать, как использовать надежные стандартные ошибки в регрессии в Stata.