Как выполнить тест даннетта в r
Апостериорный тест — это тип теста, выполняемый после ANOVA , чтобы определить, какие групповые средние значения статистически значимо отличаются друг от друга.
Если одна из исследуемых групп считается контрольной , то в качестве апостериорного теста следует использовать тест Даннетта .
В этом руководстве объясняется, как выполнить тест Даннетта в R.
Пример: тест Даннетта в R
Предположим, учитель хочет знать, могут ли два новых метода обучения улучшить результаты тестов ее учеников. Чтобы проверить это, она случайным образом делит свой класс из 30 учеников на следующие три группы:
- Контрольная группа: 10 студентов.
- Новое техническое исследование 1: 10 студентов
- Новое техническое исследование 2: 10 студентов
После недели использования назначенной им методики обучения каждый студент сдает один и тот же экзамен.
Мы можем использовать следующие шаги в R, чтобы создать набор данных, визуализировать групповые средние, выполнить однофакторный дисперсионный анализ и, наконец, выполнить тест Даннетта, чтобы определить, какой новый метод исследования (если таковой имеется) дает результаты, отличные от контрольной группы. .
Шаг 1: Создайте набор данных.
Следующий код показывает, как создать набор данных, содержащий результаты экзаменов всех 30 студентов:
#create data frame data <- data.frame(technique = rep (c("control", "new1", "new2"), each = 10 ), score = c(76, 77, 77, 81, 82, 82, 83, 84, 85, 89, 81, 82, 83, 83, 83, 84, 87, 90, 92, 93, 77, 78, 79, 88, 89, 90, 91, 95, 95, 98)) #view first six rows of data frame head(data) technical score 1 control 76 2 controls 77 3 controls 77 4 controls 81 5 controls 82 6 controls 82
Шаг 2. Просмотрите результаты экзамена для каждой группы.
Следующий код показывает, как создать коробчатые диаграммы для визуализации распределения результатов экзамена для каждой группы:
boxplot(score ~ technique,
data = data,
main = "Exam Scores by Studying Technique",
xlab = "Studying Technique",
ylab = "Exam Scores",
col = "steelblue",
border = "black")
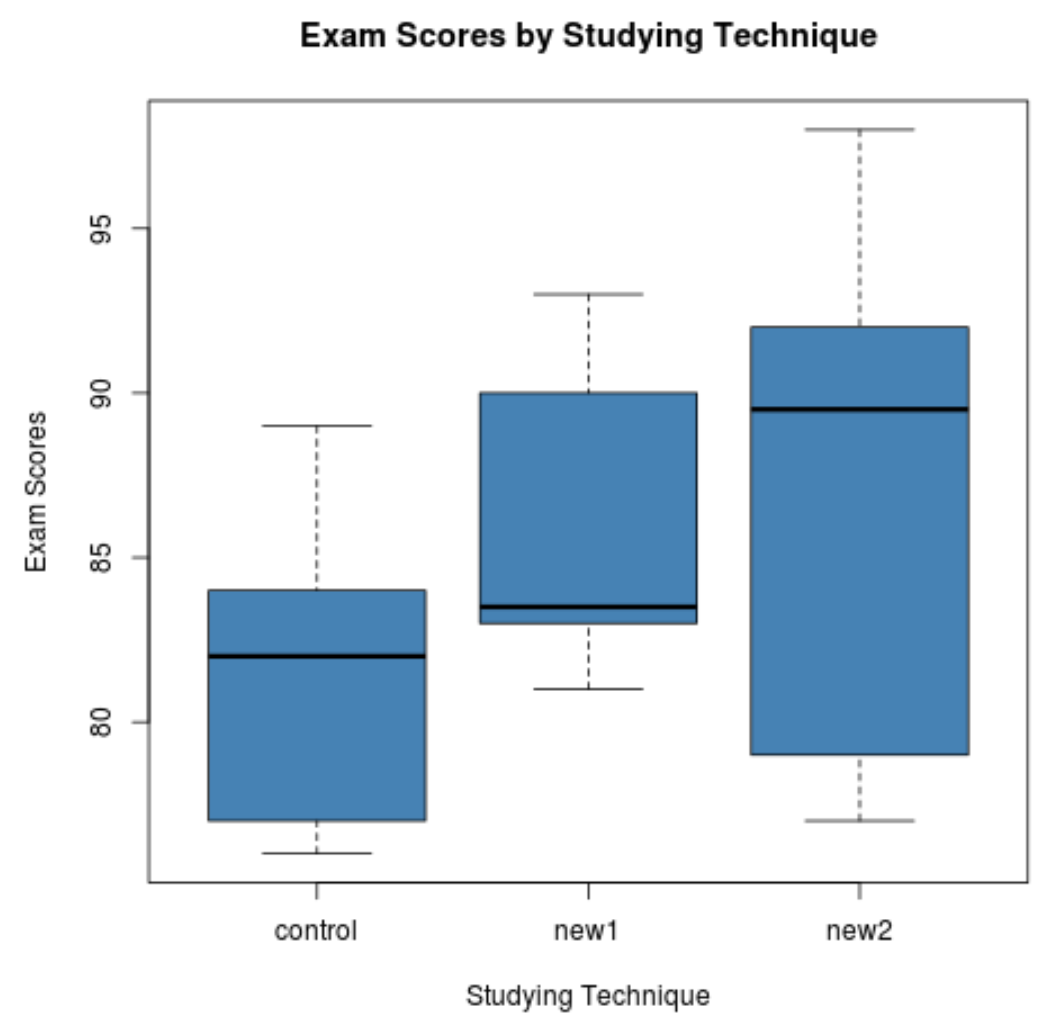
Только из коробчатых диаграмм мы видим, что распределение экзаменационных баллов сильно различается для каждого метода обучения. Затем мы выполним однофакторный дисперсионный анализ, чтобы определить, являются ли эти различия статистически значимыми.
Связанный: Как построить несколько коробчатых графиков на одной диаграмме в R
Шаг 3: Выполните односторонний дисперсионный анализ.
Следующий код показывает, как выполнить однофакторный дисперсионный анализ для проверки различий между средними баллами экзамена в каждой группе:
#fit the one-way ANOVA model model <- aov(score ~ technique, data = data) #view model output summary(model) Df Sum Sq Mean Sq F value Pr(>F) technical 2 211.5 105.73 3.415 0.0476 * Residuals 27 836.0 30.96 --- Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Поскольку общее значение p ( 0,0476 ) меньше 0,05, это указывает на то, что каждая группа не имеет одинаковый средний балл на экзамене. Далее мы проведем тест Даннетта, чтобы определить, какой метод обучения дает средние баллы на экзамене, которые отличаются от оценок в контрольной группе.
Шаг 4: Выполните тест Даннетта.
Чтобы выполнить тест Даннета в R, мы можем использовать функцию DunnettTest() из библиотеки DescTools , которая использует следующий синтаксис:
Тест Даннета (x, g)
Золото:
- x: числовой вектор значений данных (например, результаты экзамена)
- g: вектор, задающий названия групп (например, методика обучения).
Следующий код показывает, как использовать эту функцию для нашего примера:
#load DescTools library library(DescTools) #perform Dunnett's Test DunnettTest(x=data$score, g=data$technique) Dunnett's test for comparing several treatments with a control: 95% family-wise confidence level $control diff lwr.ci upr.ci pval new1-control 4.2 -1.6071876 10.00719 0.1787 new2-control 6.4 0.5928124 12.20719 0.0296 * --- Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1' '1.' 0.1 ' ' 1
Интерпретация результата следующая:
- Средняя разница в баллах на экзамене между новой методикой обучения 1 и контрольной группой составляет 4,2. Соответствующее значение p составляет 0,1787 .
- Средняя разница в баллах на экзамене между новой методикой обучения 2 и контрольной группой составляет 6,4. Соответствующее значение p составляет 0,0296 .
Основываясь на результатах, мы видим, что изучение Методики 2 является единственным методом, который дает средние баллы на экзамене, которые значительно (p = 0,0296) отличаются от показателей контрольной группы.
Дополнительные ресурсы
Введение в однофакторный дисперсионный анализ
Как выполнить односторонний дисперсионный анализ в R
Как выполнить тест Тьюки в R