Что такое точечная оценка в статистике?
Часто в статистике нас интересуют измерения параметров популяции , то есть чисел, которые описывают определенные характеристики всей популяции.
Двумя наиболее распространенными параметрами популяции являются:
1. Среднее значение численности населения: среднее значение переменной в популяции (например, средний рост мужчин в определенном городе).
2. Доля населения: доля переменной в населении (например, доля жителей округа, поддерживающих определенный закон).
Даже если мы хотим измерить эти параметры, собирать данные о каждом человеке в популяции, как правило, слишком дорого и отнимает много времени.
Вместо этого мы берем случайную выборку из совокупности и используем данные выборки для оценки параметра совокупности.
Число, которое мы используем в выборке для оценки параметра совокупности, называется точечной оценкой . Это наша наилучшая возможная оценка того, каким может быть истинный параметр популяции.
В следующей таблице показана точечная оценка, которую мы используем для оценки параметров популяции:
| Мера | Параметр популяции | Точечная оценка |
|---|---|---|
| Иметь в виду | μ (среднее значение численности населения) | x (выборочное среднее) |
| Пропорция | π (доля населения) | p (доля выборки) |
Мы хотим рассчитать параметры совокупности, но поскольку это занимает слишком много времени и стоит слишком дорого, вместо этого мы используем выборки для расчета точечных оценок.
Например, предположим, что мы хотим оценить средний вес черепах определенного вида во Флориде. Поскольку во Флориде обитают тысячи черепах, было бы чрезвычайно много времени и денег, чтобы обойти и взвесить каждую черепаху по отдельности. Вместо этого мы могли бы взять простую случайную выборку из 50 черепах и использовать средний вес черепах в этой выборке, чтобы оценить истинное среднее значение популяции:

Если среднее значение выборки составляет 150,4 фунта, то наша точечная оценка истинного среднего значения численности всего вида составит 150,4 фунта.
Важность репрезентативных выборок
Когда мы собираем выборку из популяции, в идеале мы хотим, чтобы выборка напоминала «мини-версию» нашей популяции.
Выборка считается репрезентативной для совокупности, если характеристики индивидов в выборке близко соответствуют характеристикам особей в генеральной совокупности.
Когда это происходит, мы можем с уверенностью обобщить результаты выборки на генеральную совокупность в целом и сказать, что оценка точки выборки является несмещенной оценкой истинного параметра генеральной совокупности.
Точечные оценки и доверительные интервалы
Хотя точечная оценка представляет собой наилучшую возможную оценку истинного параметра популяции, она вряд ли точно соответствует параметру популяции.
В нашем предыдущем примере не гарантируется, что средний вес черепах в выборке точно соответствует среднему весу черепах во всей популяции. Например, мы можем выбрать выборку, полную черепах с небольшим весом, или, может быть, выборку, полную тяжелых черепах.
Итак, чтобы уловить эту неопределенность, мы можем создать доверительный интервал — диапазон значений, который может содержать параметр совокупности с определенным уровнем достоверности.
Например, мы можем использовать среднее значение выборки в 150,4 фунта, чтобы оценить истинный средний вес черепах. Тогда наш доверительный интервал будет представлять собой диапазон значений — возможно, от 145 до 155,8 фунтов.
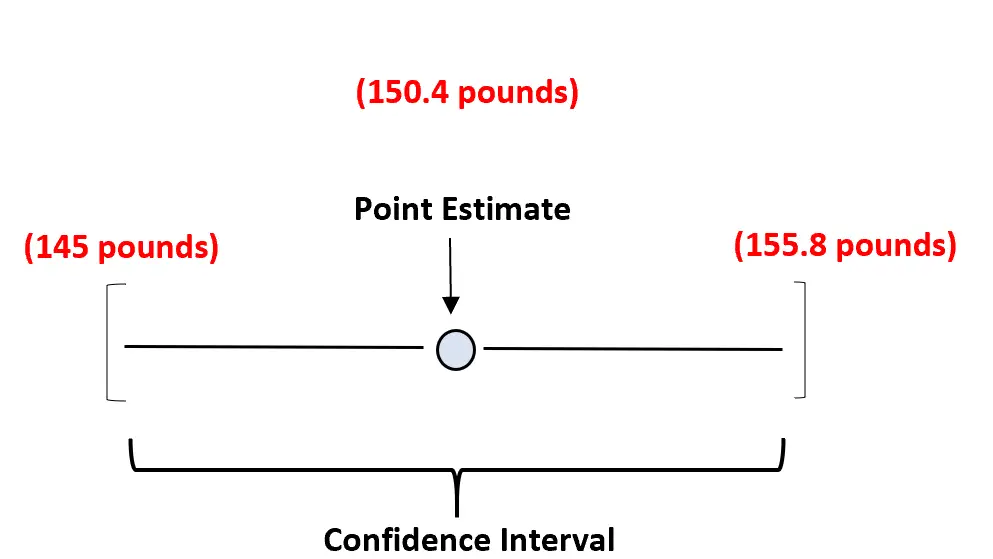
Наша точечная оценка — это наша лучшая оценка истинного среднего веса населения, а доверительный интервал обеспечивает диапазон значений, которые могут содержать истинный средний вес населения.
Подробнее о доверительных интервалах можно узнать здесь .
Дополнительные ресурсы
Статистика против. параметры: в чем разница?
Население против. образец: в чем разница?
Введение в доверительные интервалы