Функция вероятности

В этой статье объясняется, что такое функции вероятности. Таким образом, вы узнаете значение функции вероятности, ее свойства и конкретный пример расчета функции вероятности. Дополнительно представлены отличия функции вероятности от других типов вероятностных функций.

Что такое функция вероятности?

Функция вероятности , также называемая функцией массы вероятности , представляет собой математическую функцию, описывающую вероятность того, что дискретная случайная величина примет определенное значение.

То есть функция вероятности возвращает вероятность того, что дискретная переменная точно равна значению.

Например, вероятность выпадения любого числа при бросании игральной кости равна 1/6 (игральная кость имеет шесть сторон), поэтому функция вероятности, связанная с этим пространством выборки, будет равна 1/6 для n независимо от того, какое значение.

Свойства функции вероятности

Функции вероятности обладают следующими свойствами:

• Вероятности не могут быть отрицательными, поэтому функция вероятности равна нулю или положительна для любого значения x.

• Аналогично, максимальная вероятность равна единице, что означает, что событие произойдет всегда. Следовательно, максимальное значение функции вероятности равно 1.

• Наконец, сумма всех значений функции вероятности дает 1, поскольку это сумма всех вероятностей в выборочном пространстве.

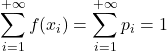
Пример функции вероятности

Теперь, когда мы знаем определение и характеристики функции вероятности, давайте посмотрим на пример вероятностной функции этого типа.

• Рассчитайте вероятности выпадения орла 0, 1, 2, 3 и 4 раза, сделав четыре независимых подброса монеты. Затем постройте график найденной функции вероятности.

Прежде всего, мы должны рассчитать вероятности выпадения решки, для этого мы должны разделить возможные случаи на общее количество случаев. Вы можете увидеть расчет всех вероятностей в следующей таблице:

И как только мы вычислили все вероятности, мы можем представить значения функции вероятности на графике:

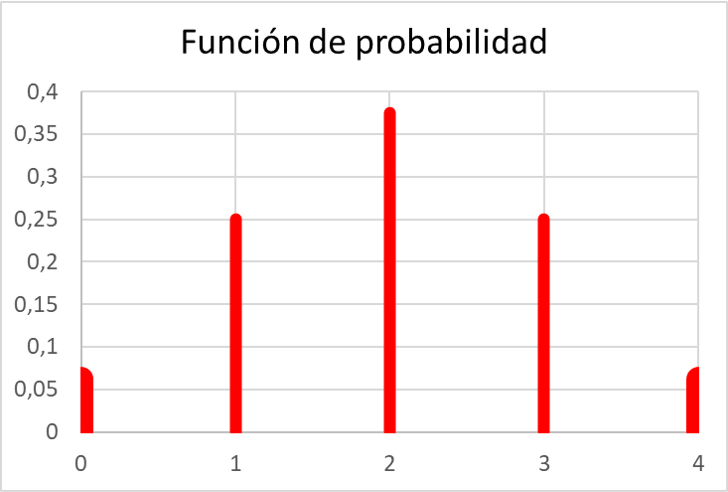
Как видите, вероятностная функция в упражнении отвечает всем свойствам функции вероятности, поскольку все ее значения находятся в диапазоне от 0 до 1 и при этом сумма всех ее значений эквивалентна 1.

Функция вероятности и функция плотности

В этом разделе мы увидим разницу между функцией вероятности и функцией плотности, поскольку это два типа вероятностных функций, которые имеют одну и ту же цель, но используются в разных случаях.

Разница между функцией вероятности и функцией плотности заключается в типе переменной, которую описывают вероятности. Функция вероятности используется для определения вероятностей дискретной переменной, а функция плотности используется для определения вероятностей непрерывной переменной.

Итак, в зависимости от переменной используется функция вероятности или функция плотности.

Чтобы узнать больше о функции плотности, нажмите на следующую ссылку:

Функция вероятности и функция распределения

Разница между функцией вероятности и функцией распределения заключается в типе вероятности, которую они определяют. Функция вероятности указывает вероятность того, что переменная примет определенное значение, а функция распределения описывает кумулятивную вероятность переменной.

Поэтому функция распределения рассчитывается из функции вероятности.

В качестве примера по следующей ссылке вы можете увидеть расчет функции распределения для получения орла в результате четырех бросков монеты на основе функции вероятности, найденной в упражнении выше.