Функция плотности

К бенджамин андерсон 5 августа, 2023 Вероятность 0 комментариев

В этой статье вы узнаете, что такое функция плотности, как рассчитывается вероятность на основе функции плотности и характеристики этой вероятностной функции. Кроме того, вы сможете увидеть, в чем разница между функцией плотности и функцией распределения.

Что такое функция плотности?

Функция плотности , также называемая функцией плотности вероятности , представляет собой математическую функцию, которая описывает вероятность того, что непрерывная случайная величина принимает определенное значение.

Другими словами, функция плотности, связанная с переменной, математически определяет вероятность того, что переменная примет значение.

Например, предположим, что вероятность того, что взрослый человек ростом выше 1,80 м в популяции составляет 35%, тогда функция плотности будет указывать вероятность 35% при расчете указанной вероятности.

Иногда функцию плотности вероятности сокращают как PDF.

Вычислите вероятность с помощью функции плотности

Чтобы найти вероятность того, что непрерывная переменная примет значение в интервале, необходимо вычислить интеграл от функции плотности, связанной с указанной переменной, между пределами интервала.

$\displaystyle P[a\leq X\leq b]=\int_a^b f(x)dx$

Золото

$f(x)$

— функция плотности непрерывной случайной величины.

Другими словами, вероятность того, что переменная примет значение в интервале, эквивалентна площади под функцией плотности в этом интервале.

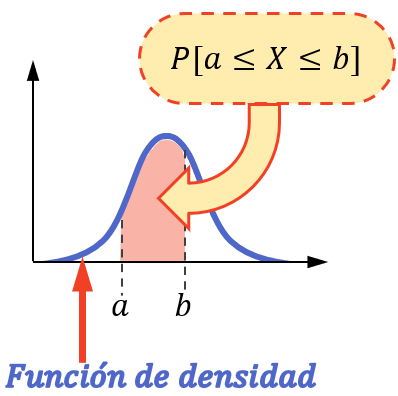
Обратите внимание, что расчет вероятности можно выполнить таким образом только в том случае, если статистическая переменная подчиняется непрерывному распределению, например нормальному распределению, экспоненциальному распределению, распределению Пуассона и т. д.

Свойства функции плотности

Функция плотности обладает следующими свойствами:

Значение функции плотности равно нулю или положительному для любого значения x.

$f(x)\geq 0$

Кроме того, максимальное значение функции плотности равно 1.

$f(x)\leq 1$

Фактически, общая площадь под графиком функции плотности всегда эквивалентна 1 независимо от переменной, поскольку соответствует множеству всех вероятностей.

$\displaystyle \int_{-\infty}^{+\infty} f(x)dx=1$

Как объяснялось в предыдущем разделе, вероятность того, что непрерывная переменная принимает значение в интервале, вычисляется с помощью интеграла функции плотности в этом интервале.

$\displaystyle P[a\leq X\leq b]=\int_a^b f(x)dx=F(b)-F(a)$

Функция плотности и функция распределения

В этом последнем разделе мы увидим, чем отличаются функция плотности и функция распределения, поскольку это два типа вероятностных функций, которые обычно путают.

Математически функция распределения эквивалентна интегралу от функции плотности , поэтому функция распределения описывает кумулятивную вероятность непрерывной переменной.

То есть образ функции распределения для любого значения равен вероятности того, что переменная примет это значение или меньшее значение.

Таким образом, математическая связь между этими двумя типами функций следующая:

$\displaystyle P[X\leq a]=\int_{-\infty}^a f(x)dx=F(a)$

Золото

$f(x)$

— функция плотности и

$F(x)$

– функция распределения.

Обратите внимание, как графическое представление функции плотности меняется относительно ее функции распределения переменной, которая следует нормальному распределению со средним значением 1 и стандартным отклонением 0,5:

разница между функцией распределения и функцией плотности

Чтобы узнать больше о функции распространения, нажмите на ссылку ниже:

➤ См.: функция распределения.

Об авторе

бенджамин андерсон

Здравствуйте, я Бенджамин, профессор статистики на пенсии, ставший преданным преподавателем Statorials. Имея обширный опыт и знания в области статистики, я хочу поделиться своими знаниями, чтобы расширить возможности студентов с помощью Statorials. Узнать больше