Функция распределения

К бенджамин андерсон 5 августа, 2023 Вероятность 0 комментариев

В этой статье вы найдете объяснение функции распределения, способы расчета ее значений и реальный пример функции распределения. Кроме того, вы сможете увидеть различия между функцией распределения и функцией плотности.

Что такое функция распределения?

Функция распределения , также называемая кумулятивной функцией распределения , представляет собой математическую функцию, которая указывает кумулятивную вероятность распределения. То есть образ функции распределения для любого значения равен вероятности того, что переменная примет это значение или меньшее значение.

Кумулятивную функцию распределения также можно обозначать аббревиатурой FDA, хотя ее обычным обозначением является заглавная буква F.

Таким образом, функция распределения определяется следующей формулой:

$F(x)=P[X\leq x]$

Как рассчитать функцию распределения

Затем мы объясним, как рассчитать значение функции распределения в зависимости от того, является ли распределение вероятностей дискретным или непрерывным.

Сдержанная коробка

Если случайная величина дискретна, кумулятивная функция распределения равна сумме вероятностей всех значений, равных или меньших x .

$\displaystyle F(x)=P[X\leq x]=\sum_{u\leq x}f(u)$

Золото

$f(u)$

— функция вероятности, связанная с дискретной переменной.

Продолжающееся дело

Если случайная величина непрерывна, кумулятивная функция распределения эквивалентна интегралу функции плотности от минус бесконечности до рассматриваемого значения.

$\displaystyle F(x)=P[X\leq x]=\int_{-\infty}^{x}f(u)du$

Золото

$f(u)$

— функция плотности, связанная с непрерывной переменной.

Пример функции распределения

Теперь, когда мы знаем определение функции распределения, давайте рассмотрим практический пошаговый пример, чтобы научиться вычислять значение функции распределения.

Рассчитайте функцию распределения для случайного эксперимента по подбрасыванию монеты четыре раза.

Для решения упражнения необходимо сначала вычислить все вероятности, связанные с количеством выпавших орлов при четырех подбрасываниях монеты:

Таким образом, поскольку это дискретная переменная, для определения образа функции распределения достаточно сложить вероятности до значения рассматриваемой переменной:

$\begin{array}{l}F(X\leq 0)=f(0)=0,0625\\[4ex]\begin{aligned}F(X\leq 1)& =f(0)+f(1)\\[1.1ex] & =0,0625+0,25=0,3125\end{aligned}\\[6ex]\begin{aligned}F(X\leq 2)& =f(0)+f(1)+f(2)\\[1.1ex] & =0,0625+0,25+0,375=0,6875\end{aligned}\\[6ex]\begin{aligned}F(X\leq 3)& =f(0)+f(1)+f(2)+f(3)\\[1.1ex] & =0,0625+0,25+0,375+0,25=0,9375\end{aligned}\\[6ex]\begin{aligned}F(X\leq 4)& =f(0)+f(1)+f(2)+f(3)+f(4)\\[1.1ex] & =0,0625+0,25+0,375+0,25+0,0625=1\end{aligned}\end{array}$

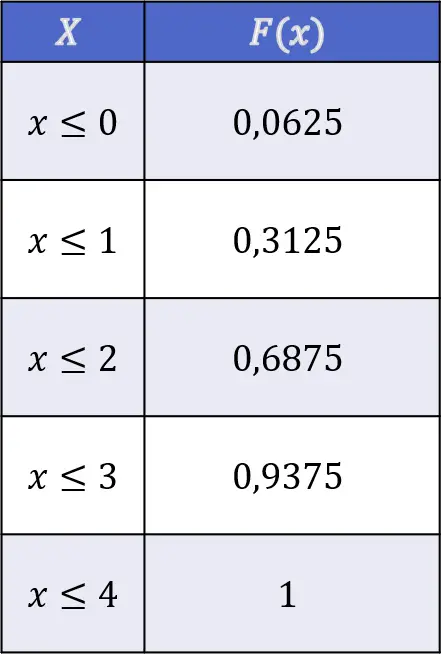
Таким образом, значения функции распределения подбрасывания головы при подбрасывании четырех независимых монет таковы:

Свойства функции распределения

Независимо от типа переменной функция распределения всегда обладает следующими свойствами:

Значение кумулятивной функции распределения находится в диапазоне от 0 до 1 включительно.

$0\leq F(x) \leq 1$

Предел функции распределения при стремлении x к бесконечности равен 1.

$\displaystyle\lim_{x\to +\infty} F(x)=1$

С другой стороны, предел функции распределения при приближении x к минус бесконечности равен нулю.

$\displaystyle\lim_{x\to -\infty} F(x)=0$

По своим характеристикам функция распределения является монотонной и неубывающей.

$x_1 \leq x_2 \implies F(x_1)\leq F(x_2)$

Кроме того, если
$a\leq b$

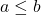
выполняются следующие уравнения.

 *** QuickLaTeX cannot compile formula:
\begin{array}{l}P(X < a) = F(a^-)\\[2ex] P(X>a)=1-F(a)\\[2ex]P(X \ge a )=1-F(a^-)\\[2ex]P(a<ul><li> Finally, if the statistical variable is continuous, the following equality is satisfied: </li></ul>[latex ]\begin{array}{l}P(a \le X < b) = \displaystyle\int_{a}^{b}f(x)\,dx = F(b)- F(a)\end{array}

*** Error message:
Missing $ inserted.
leading text: \begin{array}{l}
Please use \mathaccent for accents in math mode.
leading text: ... the statistical variable is continuous, the
Please use \mathaccent for accents in math mode.
leading text: ...iable statistic is continuous, equality
\begin{array} on input line 8 ended by \end{document}.
leading text: \end{document}
Improper \prevdepth.
leading text: \end{document}
Missing $ inserted.
leading text: \end{document}
Missing } inserted.
leading text: \end{document}
Missing \cr inserted.
leading text: \end{document}
Missing $ inserted.
leading text: \end{document}
You can't use `\end' in internal vertical mode.
leading text: \end{document}
\begin{array} on input line 8 ended by \end{document}.
leading text: \end{document}

Функция распределения и функция плотности

Наконец, мы увидим, в чем разница между функцией распределения и функцией плотности, поскольку эти два статистических понятия часто путают.

Разница между функцией распределения и функцией плотности заключается в типе вероятности, которую они определяют. Функция плотности описывает вероятность того, что переменная примет определенное значение, а функция распределения описывает кумулятивную вероятность переменной.

То есть функция распределения используется для расчета вероятности того, что переменная равна или меньше определенного значения.

Обратите внимание, что функция плотности относится только к непрерывным переменным, поэтому это различие имеет смысл только в том случае, если изучаемая переменная является непрерывной.

Обратите внимание, как меняется графическое представление функции распределения по сравнению с функцией плотности переменной, которая следует нормальному распределению со средним значением 1 и стандартным отклонением 0,5:

разница между функцией распределения и функцией плотности

Дополнительные сведения о функции плотности см. в следующей статье:

➤ См.: функция плотности

Об авторе

бенджамин андерсон

Здравствуйте, я Бенджамин, профессор статистики на пенсии, ставший преданным преподавателем Statorials. Имея обширный опыт и знания в области статистики, я хочу поделиться своими знаниями, чтобы расширить возможности студентов с помощью Statorials. Узнать больше