Как выполнить тест на соответствие хи-квадрат в spss
Критерий согласия хи-квадрат используется для определения того, соответствует ли категориальная переменная гипотетическому распределению.
В этом руководстве объясняется, как выполнить критерий согласия хи-квадрат в SPSS.
Пример: критерий согласия хи-квадрат в SPSS
Владелец магазина говорит, что в его магазин каждый день недели приходит одинаковое количество покупателей. Чтобы проверить эту гипотезу, исследователь записывает количество покупателей, пришедших в магазин за определенную неделю, и обнаруживает следующее:
- Понедельник: 50 клиентов
- Вторник: 60 клиентов
- Среда: 40 клиентов
- Четверг: 47 клиентов
- Пятница: 53 клиента
Используйте следующие шаги, чтобы выполнить критерий согласия хи-квадрат в SPSS, чтобы определить, соответствуют ли данные утверждению владельца магазина.
Шаг 1: Введите данные.
Сначала введите данные в SPSS в следующем формате:
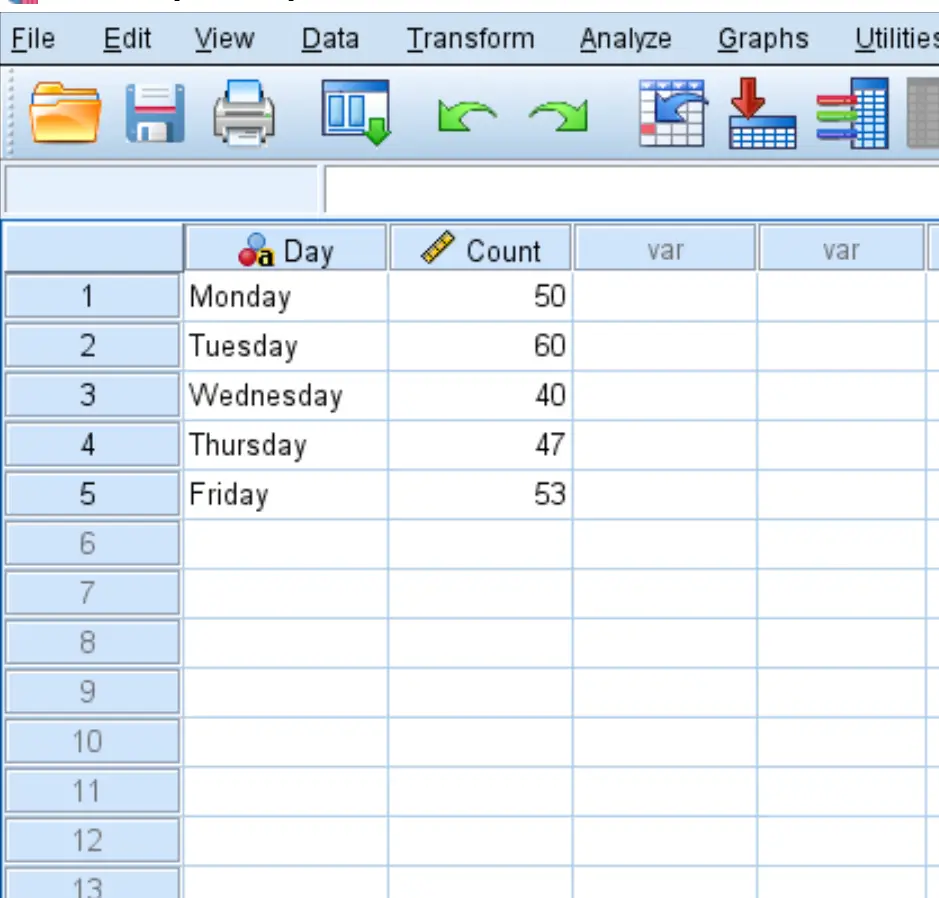
Шаг 2: Используйте утяжеленные коробки.
Чтобы тест работал правильно, нам нужно сообщить SPSS, что переменная «День» должна иметь вес по переменной «Число».
Перейдите на вкладку «Данные» , затем нажмите «Весовые случаи» :
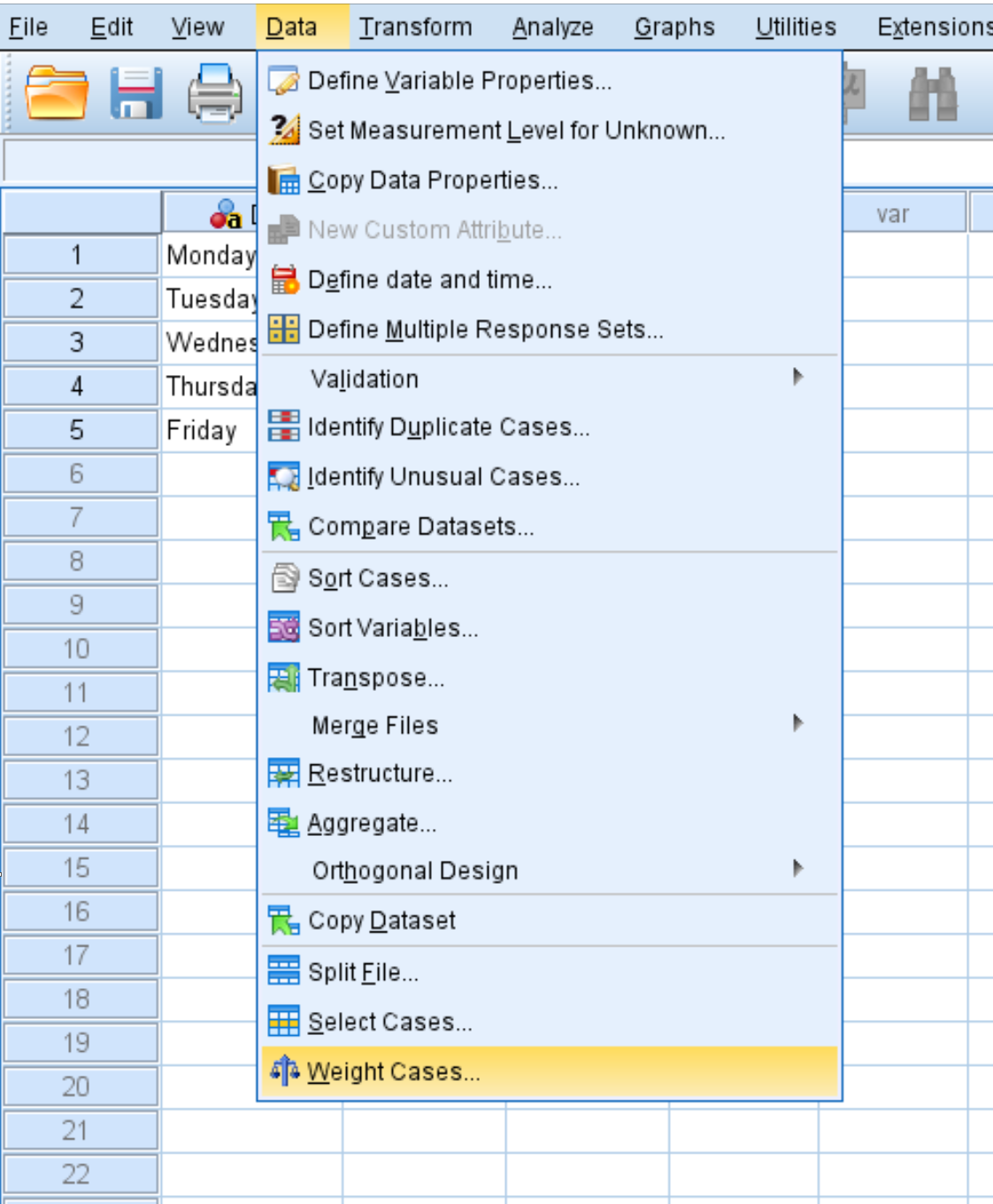
В появившемся новом окне перетащите переменную Count в область с надписью «Список тестовых переменных». Затем нажмите ОК .
Шаг 3. Выполните критерий согласия хи-квадрат.
Откройте вкладку «Анализ» , затем «Непараметрические критерии» , затем «Устаревшие диалоги» , затем «Хи-квадрат» :
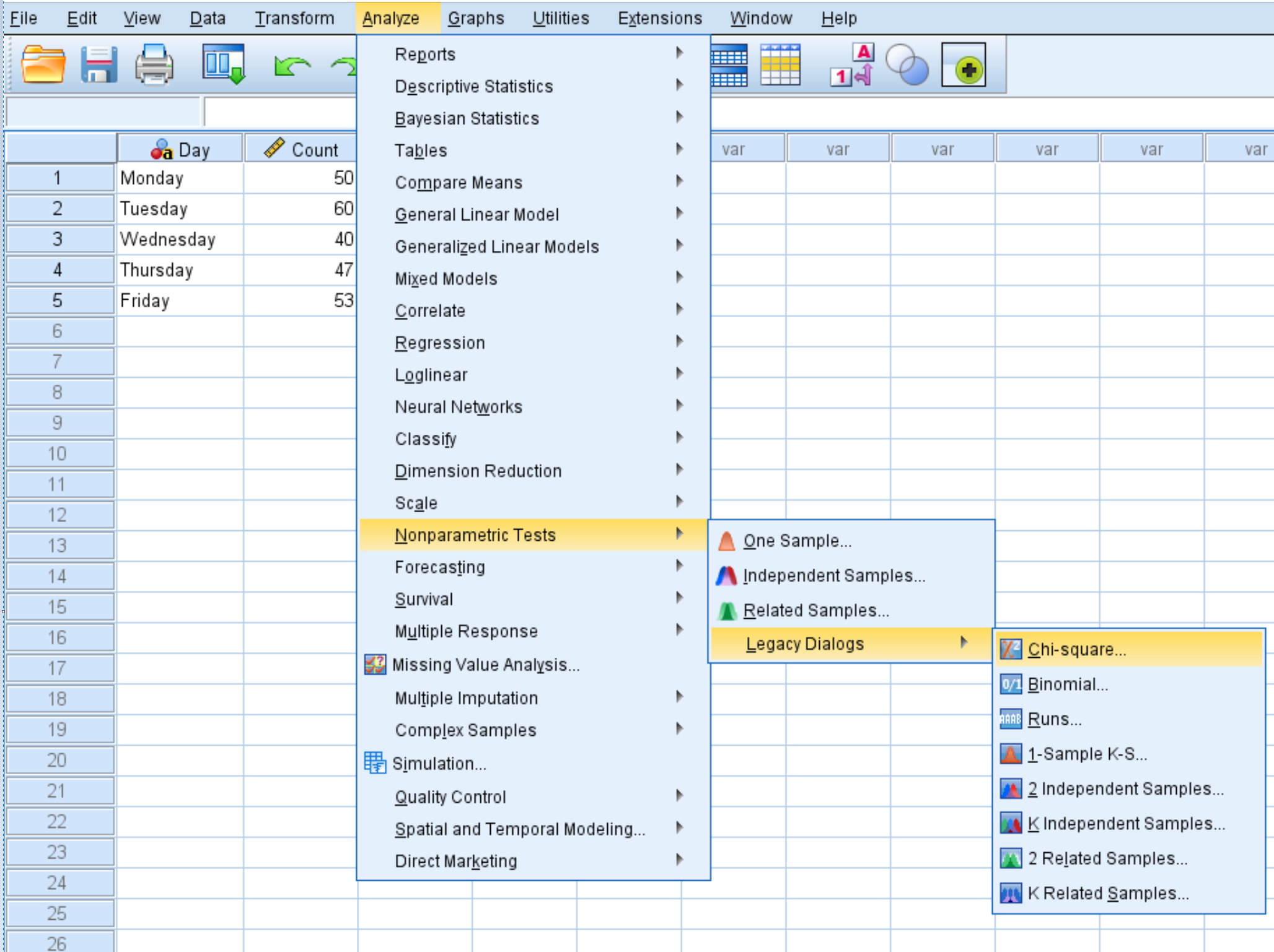
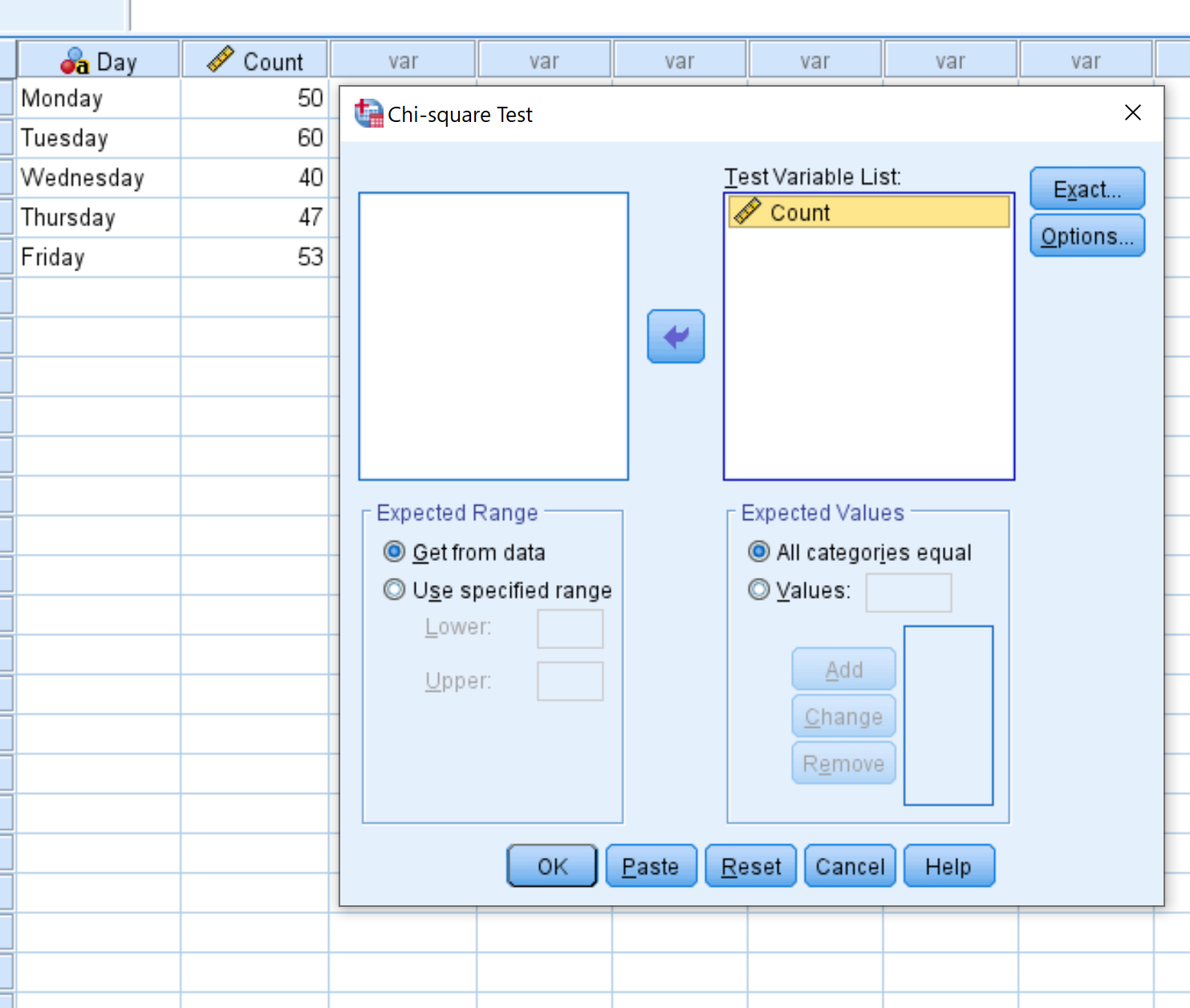
В появившемся новом окне перетащите переменную Count в область с надписью «Список тестовых переменных».
Оставьте флажок рядом с надписью «Все категории равны» , поскольку каждая из наших категорий (т. е. дней недели) имеет одинаковое ожидаемое количество посетителей каждый день. Затем нажмите ОК .

Шаг 4: Интерпретируйте результаты .
Как только вы нажмете «ОК» , появятся результаты теста согласия хи-квадрат:
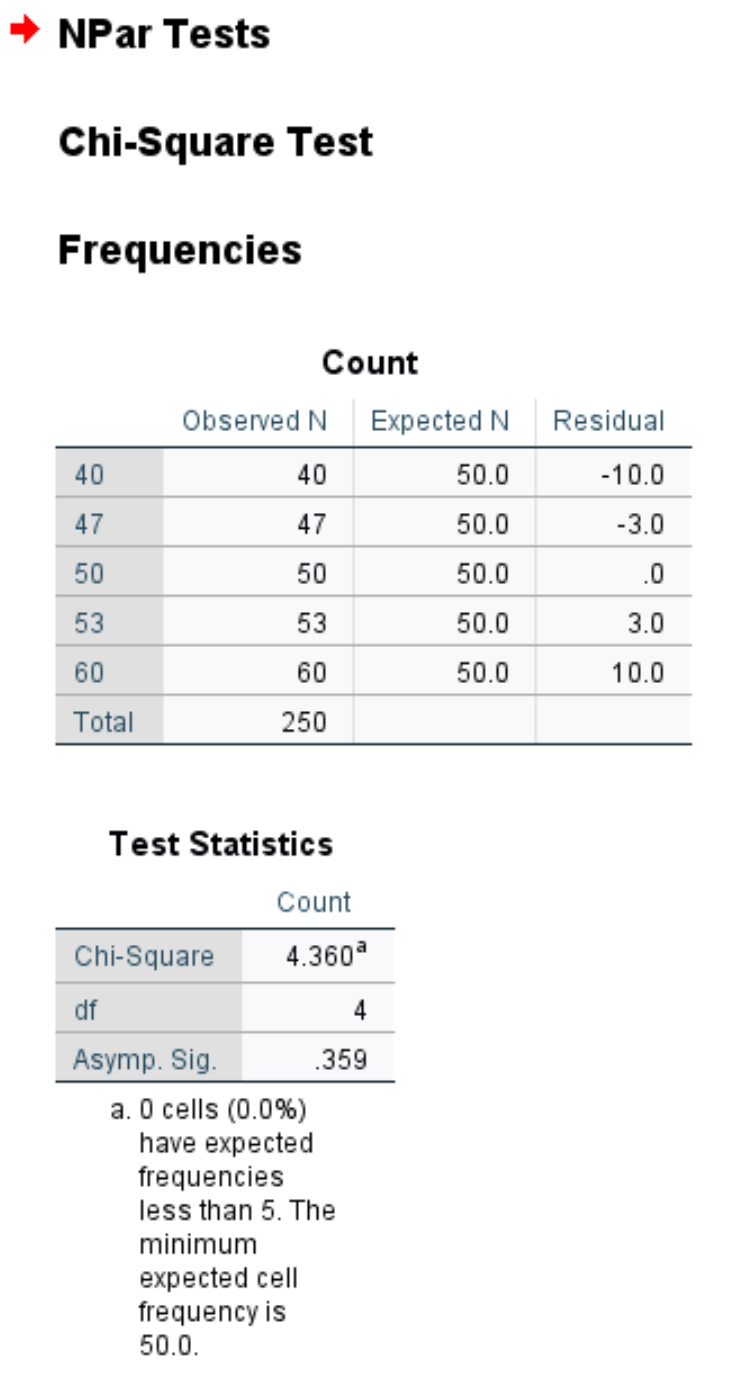
В первой таблице показано наблюдаемое и ожидаемое количество клиентов каждый день недели, а также остаток (т.е. разница) между наблюдаемым и ожидаемым.
Во второй таблице отображены следующие цифры:
Хи-квадрат: статистика теста хи-квадрат, равная 4,36.
df: Степени свободы, рассчитанные как #categories-1 = 5-1 = 4.
Асимп. Sig: значение p, соответствующее значению хи-квадрат 4,36 с 4 степенями свободы, что составляет 0,359. Это значение также можно найти с помощью калькулятора преобразования хи-квадрат в P-значение.
Поскольку значение p (0,359) не меньше 0,05, мы не можем отвергнуть нулевую гипотезу. Это означает, что у нас недостаточно доказательств, чтобы утверждать, что истинное распределение покупателей отличается от того, о котором сообщает владелец магазина.