Введение в экспоненциальное распределение

Экспоненциальное распределение — это распределение вероятностей, используемое для моделирования времени, в течение которого нам придется ждать, пока не произойдет определенное событие.

Это распределение можно использовать для ответа на такие вопросы, как:

• Как долго ритейлеру следует ждать, пока покупатель войдет в его магазин?
• Как долго ноутбук будет работать, прежде чем сломается?
• Как долго автомобильный аккумулятор будет работать, прежде чем разрядится?
• Как долго нам следует ждать следующего извержения вулкана в определенном регионе?

В каждом сценарии мы хотим рассчитать, как долго нам придется ждать, пока произойдет определенное событие. Таким образом, каждый сценарий можно смоделировать с использованием экспоненциального распределения.

Экспоненциальное распределение: PDF и CDF

Если случайная величина X подчиняется экспоненциальному распределению, то функцию плотности вероятности X можно записать:

f (x; λ) = λe ^-λx

Золото:

• λ: параметр скорости (рассчитывается как λ = 1/μ)
• e: константа, примерно равная 2,718.

Кумулятивная функция распределения

F (x; λ) = 1 – e ^-λx

На практике CDF чаще всего используется для расчета вероятностей, связанных с экспоненциальным распределением.

Например, предположим, что среднее количество минут между извержениями определенного гейзера составляет 40 минут. Насколько вероятно, что нам придется ждать извержения менее 50 минут?

Чтобы решить эту задачу, нам сначала нужно рассчитать параметр скорости:

• λ = 1/µ
• λ = 1/40
• λ = 0,025

Мы можем подставить λ = 0,025 и x = 50 в формулу CDF:

• P(X ≤ x) = 1 – e ^-λx
• Р(Х ≤ 50) = 1 – е ^-0,025(50)
• Р(Х ≤ 50) = 0,7135

Вероятность того, что следующего извержения нам придется ждать менее 50 минут, равна 0,7135 .

Визуализируйте экспоненциальное распределение

На следующем графике показана функция плотности вероятности случайной величины .

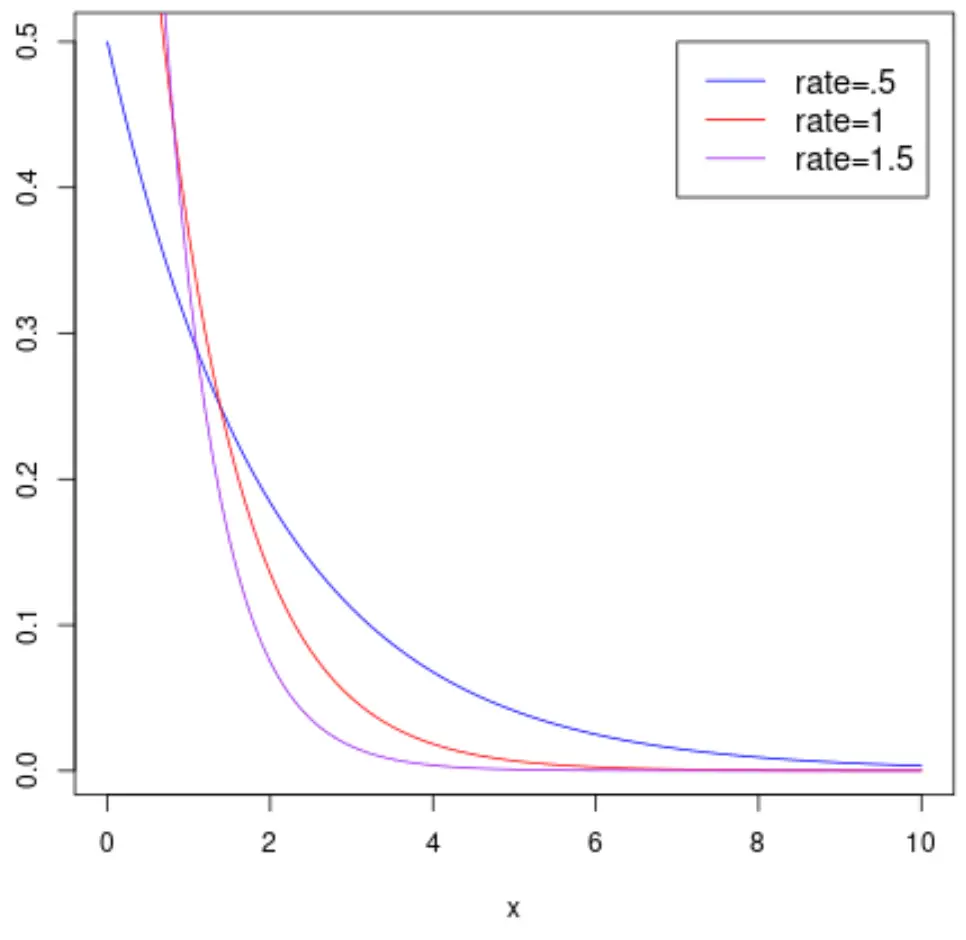
А на следующем графике показана кумулятивная функция распределения случайной величины X , которая следует экспоненциальному распределению с различными параметрами скорости:

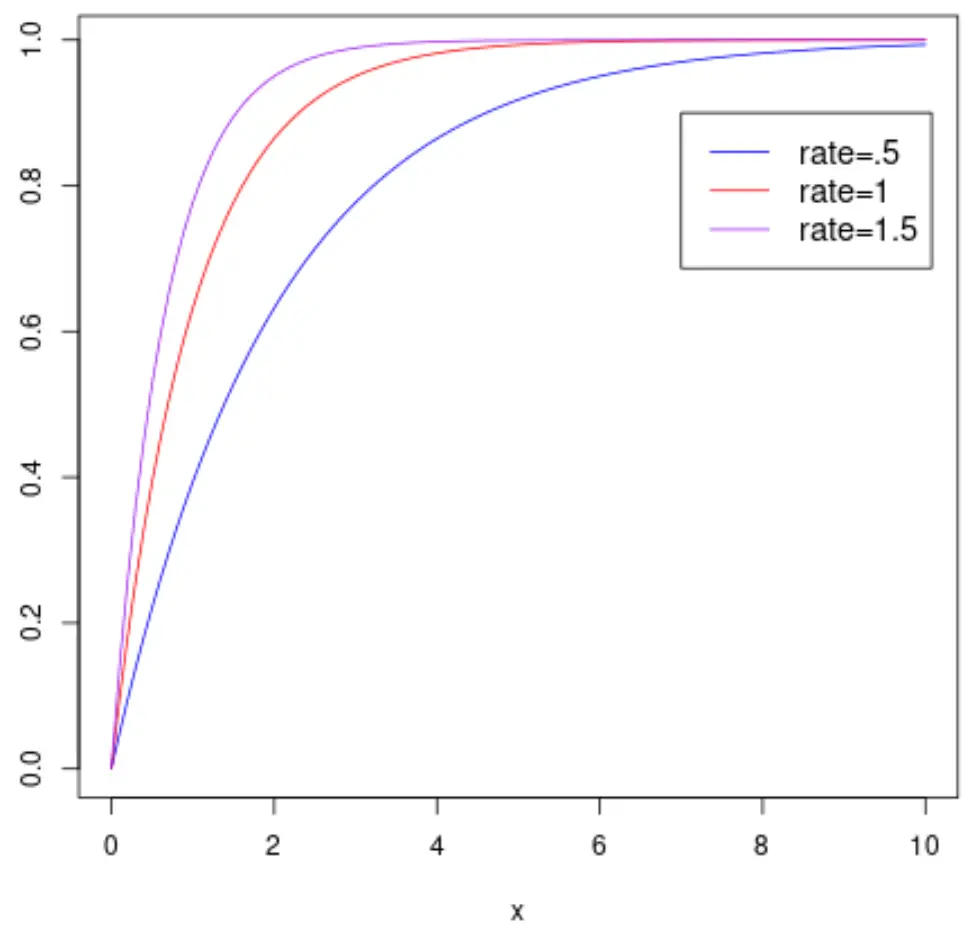
Примечание. Ознакомьтесь с этим руководством , чтобы узнать, как построить экспоненциальное распределение в R.

Свойства экспоненциального распределения

Экспоненциальное распределение обладает следующими свойствами:

• Среднее: 1 / λ
• Разница: 1 / λ ²

Например, предположим, что среднее количество минут между извержениями определенного гейзера составляет 40 минут. Мы бы рассчитали скорость как λ = 1/μ = 1/40 = 0,025.

Затем мы могли бы вычислить следующие свойства для этого распределения:

• Среднее время ожидания следующего извержения: 1/λ = 1/025 = 40.
• Изменение времени ожидания следующего извержения: 1/λ ² = 1/0,025 ² = 1600.

Примечание. Экспоненциальное распределение также обладает свойством отсутствия памяти , что означает, что вероятность возникновения будущего события не зависит от возникновения прошлых событий.

Практические задачи экспоненциального распределения

Используйте следующие практические задачи, чтобы проверить свои знания об экспоненциальном распределении.

Вопрос 1: Новый покупатель заходит в магазин в среднем каждые две минуты. После прибытия клиента определите вероятность того, что новый клиент появится менее чем через минуту.

Решение 1. Среднее время между клиентами составляет две минуты. Таким образом, ставку можно рассчитать следующим образом:

• λ = 1/µ
• λ = 1/2
• λ = 0,5

Мы можем подставить λ = 0,5 и x = 1 в формулу CDF:

• P(X ≤ x) = 1 – e ^-λx
• P(X ≤ 1) = 1 – e ^-0,5(1)
• Р(Х ≤ 1) = 0,3935

Вероятность того, что нам придется ждать прибытия следующего клиента менее минуты, равна 0,3935 .

Вопрос 2: Землетрясение происходит в среднем каждые 400 дней в определенном регионе. После землетрясения определите вероятность того, что до следующего землетрясения пройдет более 500 дней.

Решение 2. Среднее время между землетрясениями составляет 400 дней. Таким образом, ставку можно рассчитать следующим образом:

• λ = 1/µ
• λ = 1/400
• λ = 0,0025

Мы можем подставить λ = 0,0025 и x = 500 в формулу CDF:

• P(X ≤ x) = 1 – e ^-λx
• Р(Х ≤ 1) = 1 – е ^-0,0025(500)
• Р(Х ≤ 1) = 0,7135

Вероятность того, что следующего землетрясения нам придется ждать менее 500 дней, равна 0,7135. Таким образом, вероятность того, что нам придется ждать следующего землетрясения более 500 дней, равна 1 – 0,7135 = 0,2865 .

Вопрос 3. В колл-центр поступает новый звонок в среднем каждые 10 минут. После звонка клиента определите вероятность того, что новый клиент позвонит в течение 10–15 минут.

Решение 3. Среднее время между звонками составляет 10 минут. Таким образом, ставку можно рассчитать следующим образом:

• λ = 1/µ
• λ = 1/10
• λ = 0,1

Мы можем использовать следующую формулу, чтобы рассчитать вероятность того, что новый клиент позвонит в течение 10-15 минут:

• P(10 < X ≤ 15) = (1 – e ^-0,1(15) ) – (1 – e ^-0,1(10) )
• P(10 < X ≤ 15) = 0,7769 – 0,6321
• Р(10 <Х ≤ 15) = 0,1448

Вероятность того, что новый клиент позвонит в течение 10-15 минут. составляет 0,1448 .

Дополнительные ресурсы

Следующие учебные пособия знакомят с другими распространенными распределениями вероятностей.

Введение в нормальное распределение
Введение в биномиальное распределение
Введение в распределение Пуассона
Введение в равномерное распределение