График рассеяния

В этой статье объясняется, что такое диаграммы рассеяния. Таким образом, вы узнаете, для чего используется облако точек, как его создать, как его интерпретировать, а также примеры облаков точек.

Что такое облако точек?

Диаграмма рассеяния или диаграмма рассеяния — это тип статистической диаграммы, на которой набор данных из двух переменных отображается на двух декартовых координатных осях.

Поэтому диаграммы рассеяния используются для анализа взаимосвязи между двумя статистическими переменными.

Диаграммы рассеяния имеют несколько разных названий, например корреляционная диаграмма или диаграмма рассеяния .

Следует отметить, что диаграмма разброса считается одним из основных инструментов контроля качества, так же, как диаграмма Парето, диаграмма причин и следствий, блок-схема и т. д.

Как построить точечную диаграмму

Чтобы создать точечную диаграмму, вам необходимо выполнить следующие шаги:

1. Соберите статистические данные из образца, который вы хотите проанализировать. Имейте в виду, что для создания диаграммы рассеяния необходимо наличие как минимум двух количественных переменных.
2. Постройте две оси диаграммы рассеяния.
3. Определите две статистические переменные, которые будут отображены на графике.
4. Откалибруйте масштаб каждой оси графика. Для этого рекомендуется сначала найти минимум и максимум каждой переменной и на основе этих значений масштабировать каждую ось.
5. Обозначьте каждую пару данных на диаграмме рассеяния точкой.
6. Проанализируйте и интерпретируйте полученную диаграмму рассеяния.

Пример диаграммы рассеяния

После ознакомления с определением диаграммы рассеяния и теорией ее создания в этом разделе в качестве примера представлена диаграмма этого типа.

• В следующей таблице частот в качестве данных были собраны оценки по математике и статистике выборки из 20 учащихся. Постройте набор данных на диаграмме рассеяния и проанализируйте его.

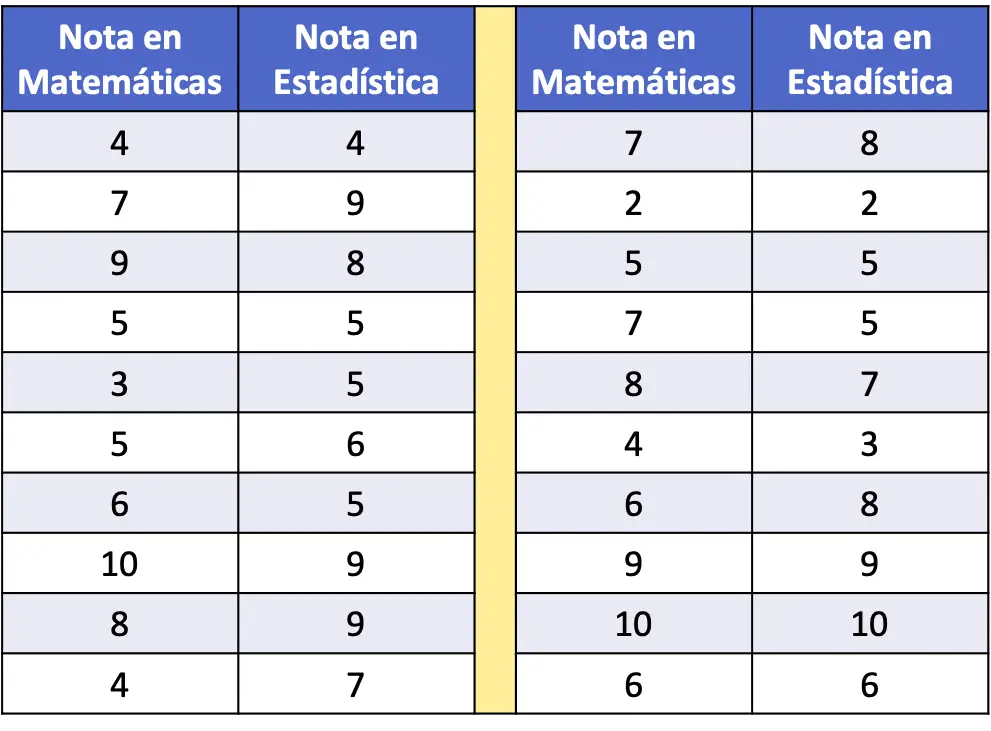
Чтобы представить ряд данных на точечной диаграмме, нам просто нужно построить две оси, откалибровать их и нанести точку на графике для каждой пары данных. Помните, что точка на графике располагается на пересечении воображаемых линий, соответствующих каждому из ее значений.

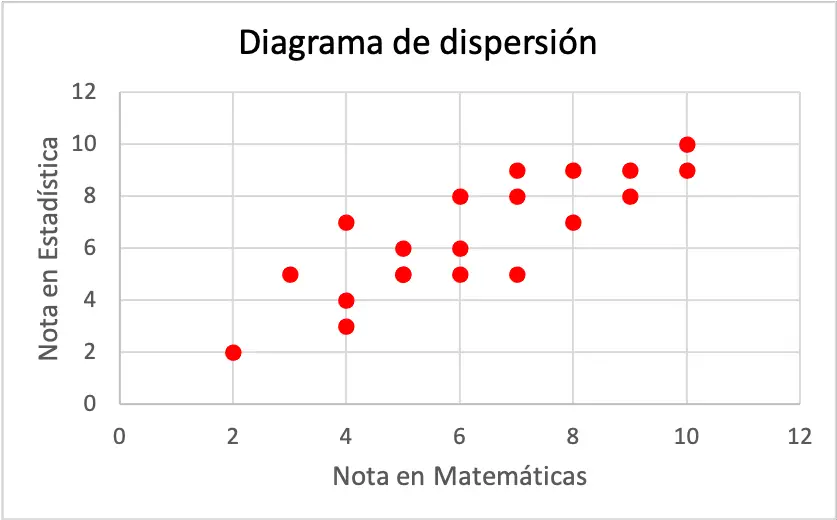
Каждая ось диаграммы рассеяния представляет переменную. Точнее, горизонтальная ось соответствует оценке, полученной по математике, а вертикальная ось соответствует оценке, полученной по статистике.

Как видно из диаграммы рассеяния, две переменные имеют положительную корреляцию, поскольку одна переменная увеличивается по мере увеличения другой переменной. Таким образом, делается вывод, что если учащийся получает более высокую оценку по математике, более вероятно, что он или она также получит более высокую оценку по статистике, и наоборот.

Однако предыдущий вывод не означает, что одна переменная является причиной другой, поскольку получение хорошей оценки по математике не гарантирует автоматически хорошую оценку по статистике без каких-либо действий, а скорее следует изучать оба предмета. В следующем разделе мы более подробно остановимся на этой концепции.

Диаграмма рассеяния и корреляция

По диаграмме разброса можно определить тип корреляции между двумя переменными:

• Прямая корреляция (или положительная корреляция) : одна переменная увеличивается, когда увеличивается и другая.
• Обратная корреляция (или отрицательная корреляция) : когда одна переменная увеличивается, другая уменьшается, и наоборот, если одна переменная уменьшается, другая увеличивается.
• Нулевая корреляция (отсутствие корреляции) : между двумя переменными нет никакой связи.

Аналогичным образом, независимо от того, является ли корреляция между двумя переменными прямой или обратной, корреляцию также можно классифицировать на основе силы или слабости связи между двумя переменными.

• Сильная корреляция: две переменные тесно связаны. Точки объединяются в облаке точек. Это облегчает определение взаимосвязи между переменными.
• Низкая корреляция : между двумя переменными существует взаимосвязь, но ее трудно определить. Точки находятся далеко друг от друга в облаке точек.

С другой стороны, корреляцию также можно рассчитать численно с использованием формулы, позволяющей математически узнать, насколько тесно связаны две разные переменные. Чтобы увидеть, как это работает, нажмите на следующую ссылку:

Имейте в виду, что даже если между двумя переменными существует корреляция, это не означает, что между ними существует причинно-следственная связь, т.е. корреляция между двумя переменными не означает, что изменение одной переменной является причиной изменения другой. переменная.

Итак, как и в случае с диаграммой рассеяния в предыдущем разделе, хотя существует положительная корреляция между оценкой по математике и оценкой по статистике, получение хорошей оценки по математике не означает получение хорошей оценки по статистике, потому что, если вы изучаете только математику, вы обязательно потерпите неудачу. в статистике. Таким образом, эти две переменные связаны, но не являются причиной и следствием.

Чтобы узнать больше, вы можете продолжить следующую публикацию:

Преимущества и недостатки облака точек

Из-за особенностей диаграммы рассеяния этот тип статистической диаграммы имеет преимущества и недостатки.

Преимущество:

• Довольно просто представить ряд данных на диаграмме рассеяния.
• Диаграмма рассеяния позволяет визуально проанализировать взаимосвязь между двумя переменными, что облегчает выводы.
• Диаграммы рассеяния также можно использовать в углубленном статистическом исследовании в качестве предварительного исследования данных.

Недостатки:

• Эти типы диаграмм бесполезны для представления качественных переменных.
• Интерпретация диаграммы рассеяния может привести к ошибочному выводу о причине и следствии между двумя переменными.
• Диаграммы рассеяния не позволяют анализировать взаимосвязь между более чем двумя переменными.