Введение в лассо-регрессию
В обычной множественной линейной регрессии мы используем набор переменных-предикторов p и переменную отклика , чтобы соответствовать модели вида:
Y = β 0 + β 1 X 1 + β 2 X 2 + … + β p
Золото:
- Y : переменная ответа
- X j : j- я прогнозируемая переменная
- β j : Среднее влияние на Y увеличения X j на одну единицу, при этом все остальные предикторы остаются фиксированными.
- ε : Погрешность
Значения β 0 , β 1 , B 2 , …, β p выбираются методом наименьших квадратов , который минимизирует сумму квадратов остатков (RSS):
RSS = Σ(y i – ŷ i ) 2
Золото:
- Σ : греческий символ, означающий сумму.
- y i : фактическое значение ответа для i-го наблюдения
- ŷ i : прогнозируемое значение ответа на основе модели множественной линейной регрессии.
Однако, когда переменные-предикторы сильно коррелируют, мультиколлинеарность может стать проблемой. Это может сделать оценки коэффициентов модели ненадежными и привести к высокой дисперсии. То есть, когда модель применяется к новому набору данных, которого она никогда раньше не видела, она, скорее всего, будет работать плохо.
Один из способов обойти эту проблему — использовать метод, известный как лассо-регрессия , который вместо этого стремится минимизировать следующее:
RSS + λΣ|β j |
где j изменяется от 1 до p и λ ≥ 0.
Этот второй член в уравнении известен как штраф за снятие средств .
Когда λ = 0, этот штрафной член не имеет никакого эффекта, и лассо-регрессия дает те же оценки коэффициентов, что и метод наименьших квадратов.
Однако по мере того, как λ приближается к бесконечности, штраф за удаление становится более влиятельным, и прогностические переменные, которые невозможно импортировать в модель, сводятся к нулю, а некоторые даже удаляются из модели.
Зачем использовать регрессию Лассо?
Преимущество лассо-регрессии перед регрессией наименьших квадратов заключается в компромиссе между смещением и дисперсией .
Напомним, что среднеквадратическая ошибка (MSE) — это показатель, который мы можем использовать для измерения точности данной модели, и он рассчитывается следующим образом:
MSE = Var( f̂( x 0 )) + [Смещение ( f̂( x 0 ))] 2 + Var(ε)
MSE = дисперсия + смещение 2 + неустранимая ошибка
Основная идея лассо-регрессии состоит в том, чтобы ввести небольшое смещение, чтобы можно было значительно уменьшить дисперсию, что приведет к снижению общей MSE.
Чтобы проиллюстрировать это, рассмотрим следующий график:

Обратите внимание, что по мере увеличения λ дисперсия значительно уменьшается при очень небольшом увеличении смещения. Однако за определенной точкой дисперсия убывает медленнее и уменьшение коэффициентов приводит к их существенному занижению, что приводит к резкому увеличению систематической ошибки.
Из графика видно, что MSE теста является самым низким, когда мы выбираем значение λ, которое обеспечивает оптимальный компромисс между смещением и дисперсией.
Когда λ = 0, штрафной член в лассо-регрессии не имеет никакого эффекта и, следовательно, дает те же оценки коэффициентов, что и метод наименьших квадратов. Однако, увеличив λ до определенной точки, мы можем уменьшить общую MSE теста.
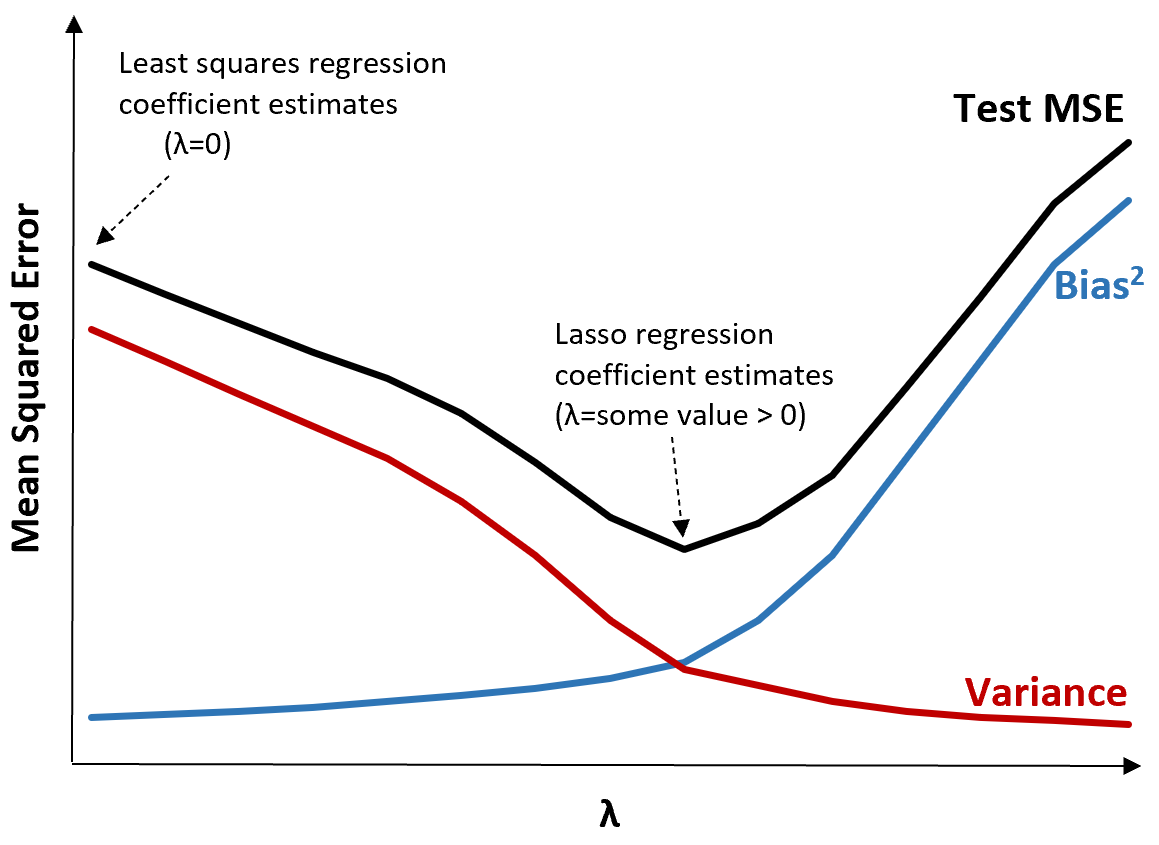
Это означает, что аппроксимация модели с помощью лассо-регрессии приведет к меньшим ошибкам теста, чем аппроксимация модели с помощью регрессии наименьших квадратов.
Лассо-регрессия против регрессии Риджа
Регрессия Лассо и регрессия Риджа известны как методы регуляризации , поскольку они оба пытаются минимизировать остаточную сумму квадратов (RSS), а также определенный штрафной член.
Другими словами, они ограничивают или регуляризируют оценки коэффициентов модели.
Однако условия штрафов, которые они используют, немного отличаются:
- Лассо-регрессия пытается минимизировать RSS + λΣ|β j |
- Ридж-регрессия пытается минимизировать RSS + λΣβ j 2
Когда мы используем гребневую регрессию, коэффициенты каждого предиктора сводятся к нулю, но ни один из них не может полностью обратиться к нулю .
И наоборот, когда мы используем лассо-регрессию, возможно, что некоторые коэффициенты станут полностью равными нулю , когда λ станет достаточно большим.
С технической точки зрения, лассо-регрессия способна создавать «разреженные» модели, то есть модели, которые включают только подмножество переменных-предикторов.
Возникает вопрос: что лучше — регрессия гребня или регрессия лассо?
Ответ: это зависит!
В тех случаях, когда значимыми являются лишь небольшое количество переменных-предикторов, лассо-регрессия имеет тенденцию работать лучше, поскольку она способна полностью свести незначимые переменные к нулю и удалить их из модели.
Однако, когда многие переменные-предикторы являются значимыми в модели и их коэффициенты примерно равны, гребневая регрессия имеет тенденцию работать лучше, поскольку она сохраняет все предикторы в модели.
Чтобы определить, какая модель наиболее эффективна для прогнозирования, мы выполняем k-кратную перекрестную проверку . Какая бы модель ни давала наименьшую среднеквадратическую ошибку (MSE), она является лучшей моделью для использования.
Шаги по выполнению лассо-регрессии на практике
Для выполнения лассо-регрессии можно использовать следующие шаги:
Шаг 1: Рассчитайте корреляционную матрицу и значения VIF для переменных-предикторов.
Во-первых, нам нужно создать корреляционную матрицу и рассчитать значения VIF (коэффициент инфляции дисперсии) для каждой переменной-предиктора.
Если мы обнаружим сильную корреляцию между переменными-предикторами и высокими значениями VIF (в некоторых текстах «высокое» значение VIF определяется как 5, а в других используется 10), то, вероятно, подойдет лассо-регрессия.
Однако, если в данных нет мультиколлинеарности, возможно, вообще нет необходимости выполнять лассо-регрессию. Вместо этого мы можем выполнить обычную регрессию по методу наименьших квадратов.
Шаг 2. Подберите модель регрессии лассо и выберите значение λ.
Как только мы определим, что лассо-регрессия подходит, мы сможем подогнать модель (используя популярные языки программирования, такие как R или Python), используя оптимальное значение λ.
Чтобы определить оптимальное значение λ, мы можем подогнать несколько моделей, используя разные значения λ, и выбрать λ как значение, которое дает наименьший тест MSE.
Шаг 3. Сравните регрессию лассо с регрессией гребня и обычной регрессией наименьших квадратов.
Наконец, мы можем сравнить нашу модель лассо-регрессии с моделью гребневой регрессии и моделью регрессии наименьших квадратов, чтобы определить, какая модель дает наименьший тест MSE с использованием k-кратной перекрестной проверки.
В зависимости от взаимосвязи между переменными-предикторами и переменной отклика вполне возможно, что одна из этих трех моделей превзойдет другие в разных сценариях.
Лассо-регрессия в R и Python
В следующих руководствах объясняется, как выполнить лассо-регрессию в R и Python:
Лассо-регрессия в R (шаг за шагом)
Лассо-регрессия в Python (шаг за шагом)