Симметричное распределение

К бенджамин андерсон 5 августа, 2023 Статистика 0 комментариев

В этой статье вы узнаете, что такое симметричные распределения, примеры симметричных распределений и как определить, является ли распределение симметричным или асимметричным.

Что такое симметричное распределение?

В статистике симметричное распределение — это распределение, которое имеет одинаковое количество значений слева от среднего и справа от среднего. Другими словами, в симметричном распределении среднее значение представляет собой ось симметрии.

Например, нормальное распределение является симметричным распределением.

Во всех симметричных распределениях среднее значение равно медиане. Но если распределение также унимодальное (статистическая мода представляет собой одно значение), среднее значение, медиана и мода эквивалентны.

Логически, чтобы полностью понять, что такое симметричное распределение, вам необходимо четко понимать, что такое среднее значение, медиана и мода. Вы можете ознакомиться со значением этих статистических понятий здесь:

➤ См.: Что такое среднее, медиана и мода?

Примеры симметричных распределений

Учитывая определение симметричного распределения, пример этого типа распределения показан ниже:

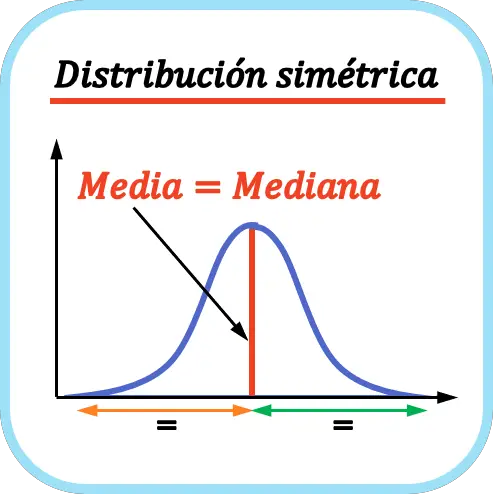
Как видно из графика, распределение симметрично, поскольку среднее значение лежит прямо посередине всех данных, то есть хвост слева от кривой такой же, как хвост справа. В этом случае среднее значение, медиана и мода одинаковы, поскольку мода унимодальная.

Двумя яркими примерами двух разных типов симметричных распределений вероятностей являются нормальное распределение и равномерное распределение, поскольку они имеют одинаковое количество значений слева и справа от среднего значения.

С другой стороны, распределение может быть также симметричным и бимодальным, то есть иметь две моды. Посмотрите на следующий пример:

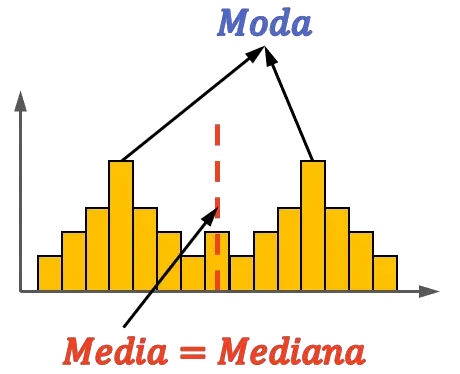
Как вы можете видеть в этом другом примере, бимодальное распределение также может быть симметричным, поскольку оно может иметь среднее значение и медиану в центре независимо от других значений. Однако в этом случае мода не обязательно должна быть равна среднему и моде.

Другие типы распределений в зависимости от их симметрии

Помимо симметричных распределений, существуют еще два типа асимметричных распределений.

Симметричное распределение : распределение имеет одинаковое количество значений слева и справа от среднего значения.
Положительно асимметричное распределение : распределение имеет больше разных значений справа от среднего значения, чем слева от него.
Отрицательно искаженное распределение : распределение имеет больше разных значений слева от среднего значения, чем справа.

Как определить, является ли распределение симметричным

Чтобы определить, является ли распределение симметричным или нет, мы должны вычислить коэффициент асимметрии Пирсона, формула которого имеет вид:

$A_p=\cfrac{\mu-Mo}{\sigma}$

Золото

$A_p$

– коэффициент Пирсона,

$\mu$

среднее арифметическое,

$Mo$

режим (статистика) и

$\sigma$

стандартное отклонение.

Таким образом, в зависимости от знака коэффициента асимметрии Пирсона распределение будет симметричным или асимметричным:

Если коэффициент асимметрии Пирсона положительный, это означает, что распределение асимметрировано положительно.
Если коэффициент асимметрии Пирсона отрицательный, это означает, что распределение искажено отрицательно.
Если коэффициент асимметрии Пирсона равен нулю, это означает, что распределение симметрично.

Однако коэффициент Пирсона можно рассчитать только в том случае, если распределение унимодальное, в противном случае необходимо использовать коэффициент асимметрии Фишера, формула которого имеет следующий вид:

$\displaystyle\gamma_1=\frac{\displaystyle \sum_{i=1}^N\left(x_i-\mu\right)^3}{N\cdot \sigma ^3}$

Золото

$\mu$

среднее арифметическое,

$\sigma$

стандартное отклонение и

$N$

общее количество данных.

Интерпретация коэффициента асимметрии Фишера идентична коэффициенту Пирсона: если он положителен, это означает, что распределение положительно асимметрично, если он отрицателен, то распределение отрицательно асимметрично, а если он равен нулю, это означает, что распределение симметрично.

Об авторе

бенджамин андерсон

Здравствуйте, я Бенджамин, профессор статистики на пенсии, ставший преданным преподавателем Statorials. Имея обширный опыт и знания в области статистики, я хочу поделиться своими знаниями, чтобы расширить возможности студентов с помощью Statorials. Узнать больше