Зависимая переменная
В этой статье объясняется, что такое зависимые переменные. Таким образом, вы узнаете, что означает зависимость переменной в математике и статистике, а также сможете увидеть несколько примеров зависимых переменных.
Что такое зависимая переменная?
Зависимая переменная — это переменная, значение которой зависит от значения другой переменной. Другими словами, значение зависимой переменной будет меняться в зависимости от значения, принимаемого независимой переменной.
В общем, зависимая переменная обычно обозначается буквой y на оси y (вертикальной оси).
Например, цена акции является зависимой переменной, которая зависит от многих других переменных, таких как экономический результат компании, количество инвесторов, последние новости компании и т. д.
Примеры зависимых переменных
Теперь, когда мы знаем определение зависимой переменной, мы увидим несколько примеров этого типа переменных, чтобы полностью понять эту концепцию.
- Здоровье человека (зависимая переменная) зависит от его питания (независимая переменная).
- На частоту сердечных сокращений человека (зависимая переменная) влияет то, насколько он высок (независимая переменная).
- Уровень удовлетворенности клиента (зависимая переменная) меняется в зависимости от качества предоставляемой услуги (независимая переменная).
- Количество загрязняющих веществ, выбрасываемых страной (зависимая переменная), зависит от промышленного производства этой страны (независимая переменная).
- Заработная плата водителя такси (зависимая переменная) варьируется в зависимости от количества поездок, которые он совершает (независимая переменная).
Зависимая переменная в математике
В математике причинно-следственная связь обычно моделируется с использованием независимой переменной и зависимой переменной. Таким образом, функция определяет математическую связь, существующую между зависимой переменной и независимой переменной.
![]()
Зависимые переменные обычно обозначаются буквой y , с другой стороны, буква x обычно используется для обозначения независимых переменных.
Например, функция y=2x указывает, что когда независимая переменная x увеличивается на одну единицу, зависимая переменная y увеличивается в два раза.
Чтобы узнать больше о математических функциях, посетите наш партнерский веб-сайт function.xyz .
Зависимая переменная в статистике
Однако на самом деле очень сложно найти связь между двумя переменными, которую можно определить с помощью точной математической функции, поскольку иногда одно и то же значение независимой переменной приводит к разным значениям зависимой переменной.
Например, иногда, изучая больше, мы получаем более низкую оценку или, наоборот, изучая меньше, мы получаем более высокую оценку. Поэтому количество часов, которые мы посвящаем учебе, — не единственный фактор, влияющий на получаемую оценку, оно также может варьироваться в зависимости от сложности экзамена или сложности изучаемого материала.
По этой причине в статистике обычно проводится множество экспериментов, чтобы определить, существует ли связь между двумя переменными, одна из которых будет независимой, а другая — зависимой. Затем полученные результаты можно представить графически, чтобы проверить, связаны ли переменные, и если да, то посмотреть, какой тип связи между ними (положительная, отрицательная, линейная, экспоненциальная и т. д.).
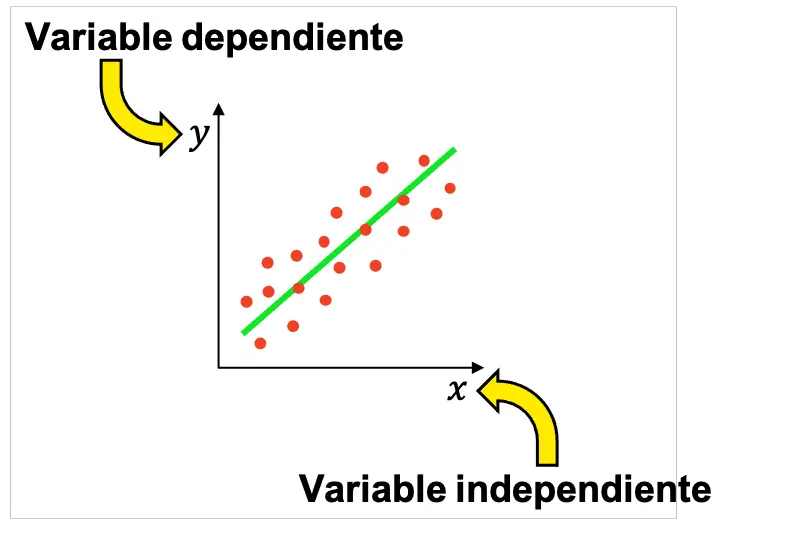
Имейте в виду, что в опросе может быть более одной независимой переменной, хотя самые основные статистические исследования проводятся с одной независимой и одной зависимой переменной.
После проведения статистического исследования можно рассчитать математическую функцию, чтобы сделать аппроксимацию и, таким образом, смоделировать взаимосвязь между переменными. Обычно сначала создается статистическая модель, а затем математическая модель.