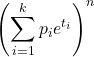Полиномиальное распределение
В этой статье объясняется, что такое полиномиальное распределение в статистике. Итак, вы найдете определение полиномиального распределения, какова его формула, решаемое упражнение и каковы свойства этого типа распределения вероятностей. Дополнительно вы сможете посчитать вероятность полиномиального распределения с помощью онлайн-калькулятора.
Что такое полиномиальное распределение?
Полиномиальное распределение (или полиномиальное распределение ) — это распределение вероятностей, которое описывает вероятность того, что несколько взаимоисключающих событий произойдут заданное количество раз после нескольких испытаний.
То есть, если случайный эксперимент может привести к трем или более исключительным событиям и известна вероятность того, что каждое событие произойдет отдельно, полиномиальное распределение используется для расчета вероятности того, что при выполнении нескольких экспериментов произойдет определенное количество событий. время каждый раз.
Таким образом, полиномиальное распределение является обобщением биномиального распределения.
Формула полиномиального распределения
Чтобы вычислить вероятность полиномиального распределения, необходимо сначала определить частное между факториалом общего количества данных и факториалами количества появлений каждого события, а результат умножить на произведение вероятности каждого события. доведено до числа повторений указанного события.
Другими словами, формула полиномиального распределения выглядит следующим образом:

Золото:
-
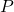
– вероятность рассчитанного полиномиального распределения.
-

общее количество выполненных тестов.
-

сколько раз происходит событие

.
-

это вероятность того, что событие произойдет

.
👉 Вы можете использовать калькулятор ниже, чтобы рассчитать вероятность переменной, которая подчиняется полиномиальному распределению.
Пример полиномиального распределения
Чтобы завершить понимание концепции полиномиального распределения, ниже вы решили пример расчета вероятности полиномиального распределения.
- В магазине продаются три разных товара. Когда покупатель совершает покупку, вероятность того, что это будет товар А, товар Б или товар С, составляет 30%, 15% и 55% соответственно. Найти вероятность того, что из 8 единиц товара 2 из них будут товара А, 1 — товара В и 5 — товара С.
Определенная проблема определяется полиномиальным распределением, поэтому необходимо применить формулу для этого типа распределения вероятностей:
![]()
Итак, подставляем данные из задачи в формулу и выполняем расчет вероятности:
![]()
Таким образом, вероятность того, что произойдет то, что говорится в постановке задачи, составляет 11,4%.
Калькулятор полиномиального распределения
Запишите количество появлений каждого события в первом поле и в том же порядке вероятность появления каждого события во втором поле. Затем введите общее количество попыток, сделанных в последнем пустом поле.
Данные должны быть разделены пробелом и введены с использованием точки в качестве десятичного разделителя.
Свойства полиномиального распределения
Полиномиальное распределение имеет следующие характеристики:
- В полиномиальном распределении ожидаемое значение количества раз, когда событие i произойдет при выполнении n испытаний, равно общему количеству выполненных испытаний, умноженному на вероятность возникновения события.
![]()
- В полиномиальном распределении дисперсия события i рассчитывается с использованием следующего выражения:
![]()
- Аналогичным образом, ковариация между двумя событиями эквивалентна произведению общего количества испытаний, умноженному на вероятность каждого события, умноженному на -1:
![]()
- Производящая функция момента для полиномиального распределения: