Когда следует использовать полиномиальную регрессию?

Полиномиальная регрессия — это метод, который мы можем использовать для подбора модели регрессии, когда связь между переменными-предикторами и переменной ответа является нелинейной.

Модель полиномиальной регрессии принимает следующую форму:

Y = β ₀ ⁺ β ₁ X + β ₂ X ² + … + β _h

На практике существует три простых способа определить, следует ли вам использовать полиномиальную регрессию по сравнению с более простой моделью, такой как линейная регрессия .

1. Создайте диаграмму рассеяния переменной-предиктора и переменной ответа.

Самый простой способ определить, следует ли использовать полиномиальную регрессию, — это создать простую диаграмму рассеяния переменной-предиктора и переменной отклика.

Например, предположим, что мы хотим использовать переменную-предиктор «учебные часы», чтобы спрогнозировать оценку, которую студент получит на выпускном экзамене.

Прежде чем подобрать регрессионную модель, мы можем сначала построить диаграмму рассеяния изученных часов в зависимости от результатов экзамена. Предположим, что наша диаграмма рассеяния выглядит так:

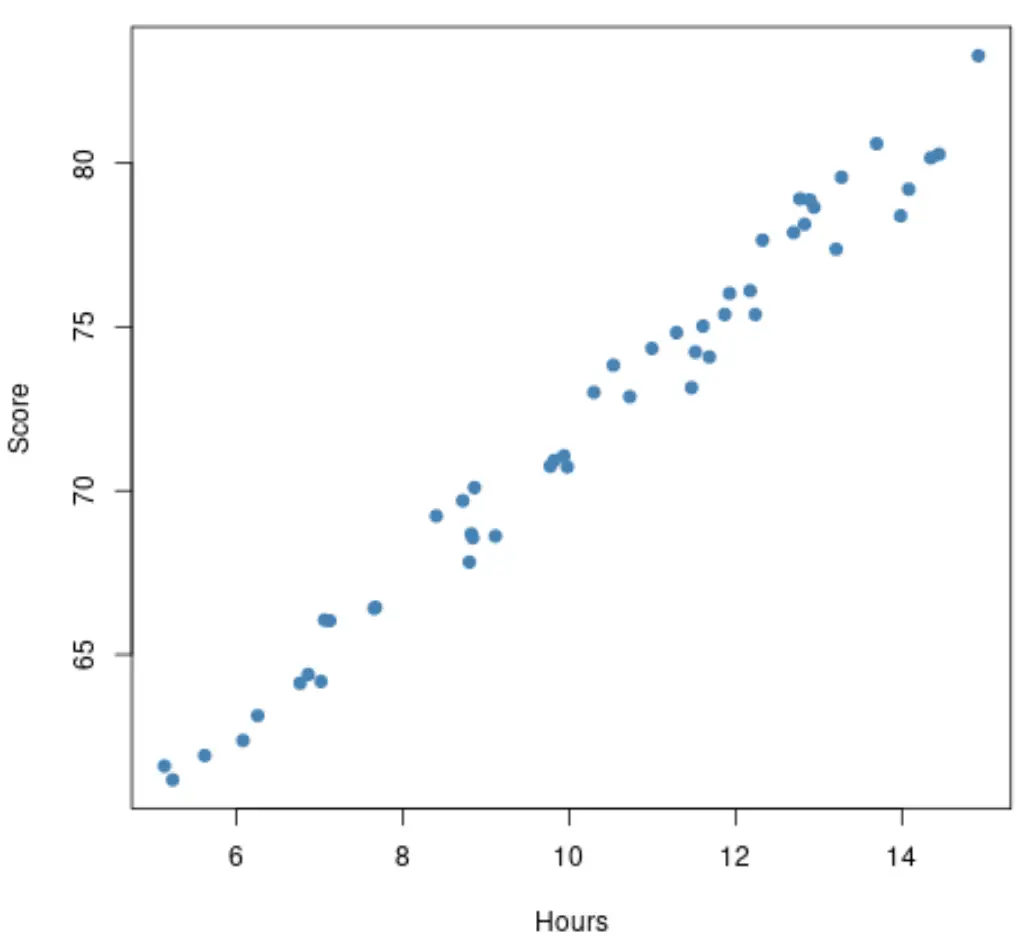
Связь между учебными часами и результатами экзаменов кажется линейной , поэтому имело бы смысл подогнать к этому набору данных простую модель линейной регрессии.

Однако давайте предположим, что диаграмма рассеяния на самом деле выглядит следующим образом:

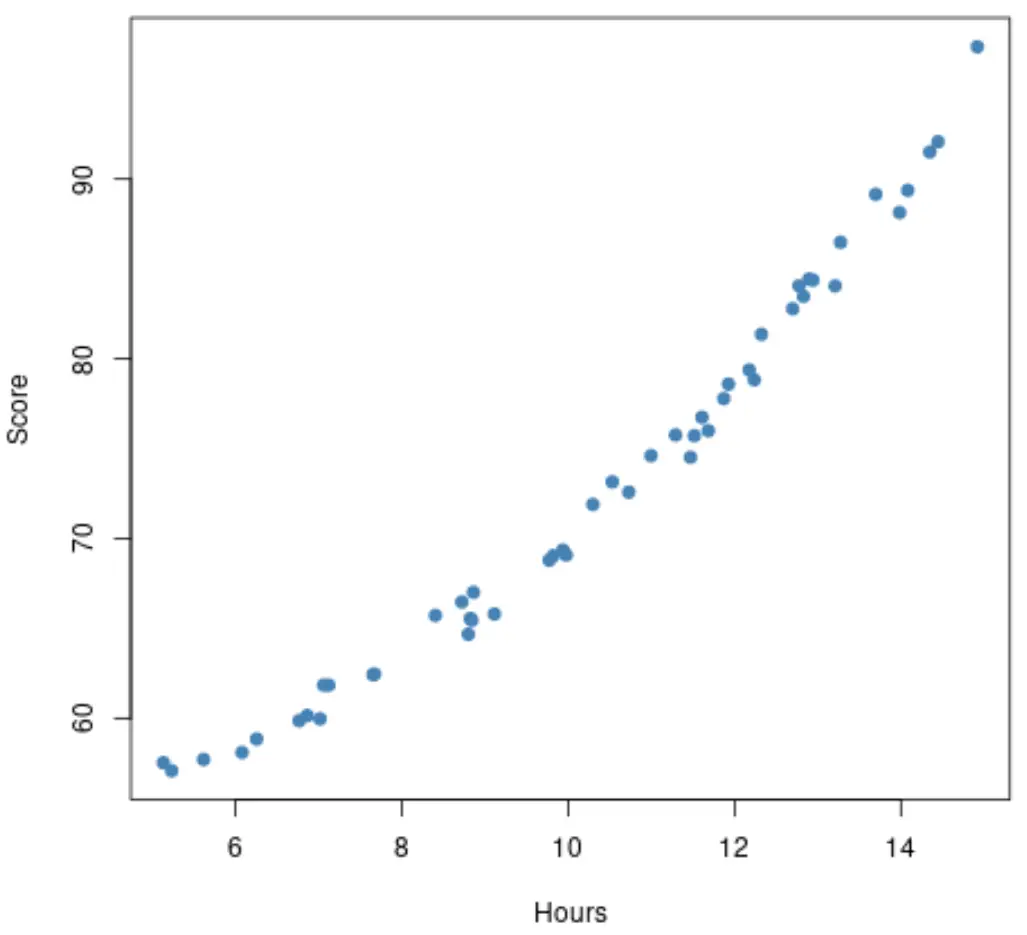
Эта зависимость кажется немного более нелинейной , что говорит нам о том, что вместо этого, возможно, было бы разумно использовать модель полиномиальной регрессии.

2. Создайте график подобранных и остаточных значений.

Другой способ определить, следует ли вам использовать полиномиальную регрессию, — это подогнать модель линейной регрессии к набору данных, а затем создать график сопоставления подобранных значений с остатками модели.

Если в остатках наблюдается явная нелинейная тенденция, это указывает на то, что полиномиальная регрессия может обеспечить лучшее соответствие данным.

Например, предположим, что мы подгоняем модель линейной регрессии, используя часы обучения в качестве предикторной переменной и оценку экзамена в качестве переменной ответа, а затем создаем следующий график подобранных значений в зависимости от остатков:

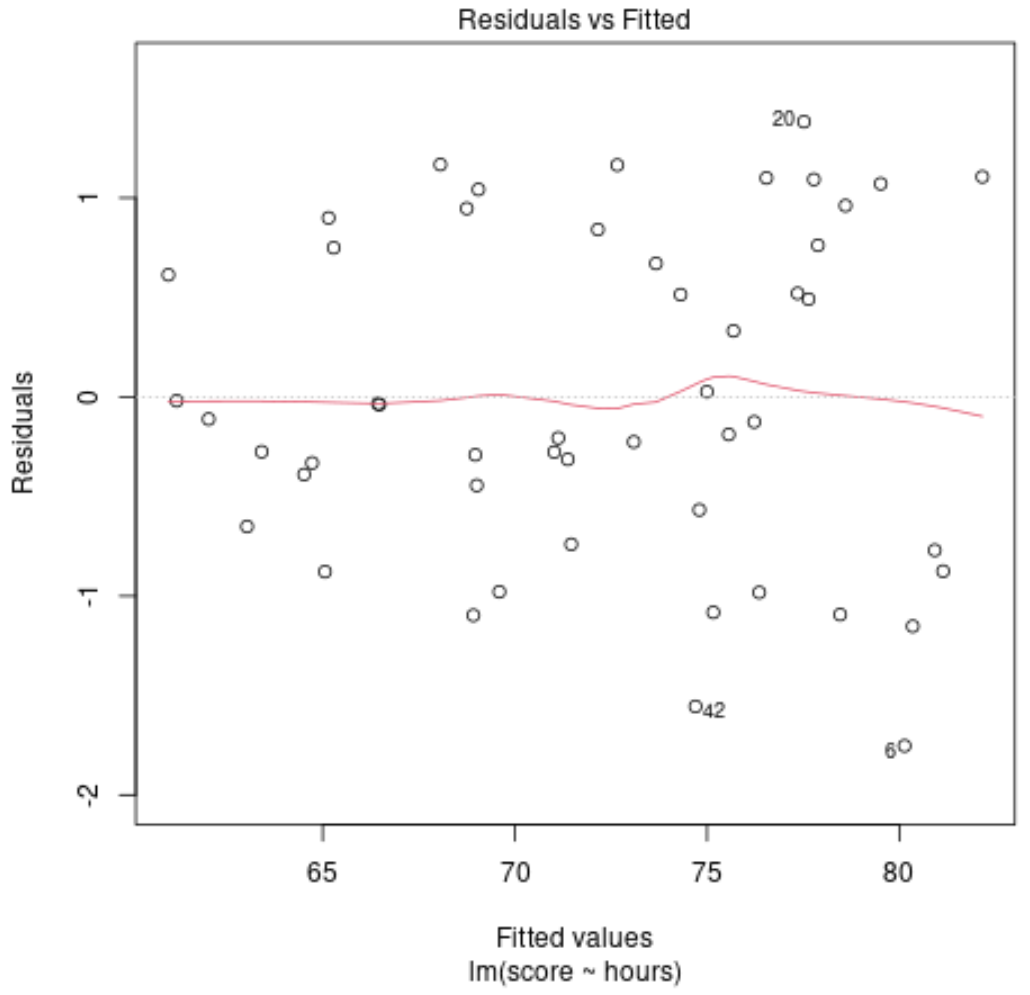
Остатки случайным образом разбросаны вокруг нуля без четкой закономерности, что указывает на то, что линейная модель обеспечивает подходящее соответствие данным.

Однако давайте предположим, что наш график подобранных значений в зависимости от остатков на самом деле выглядит следующим образом:

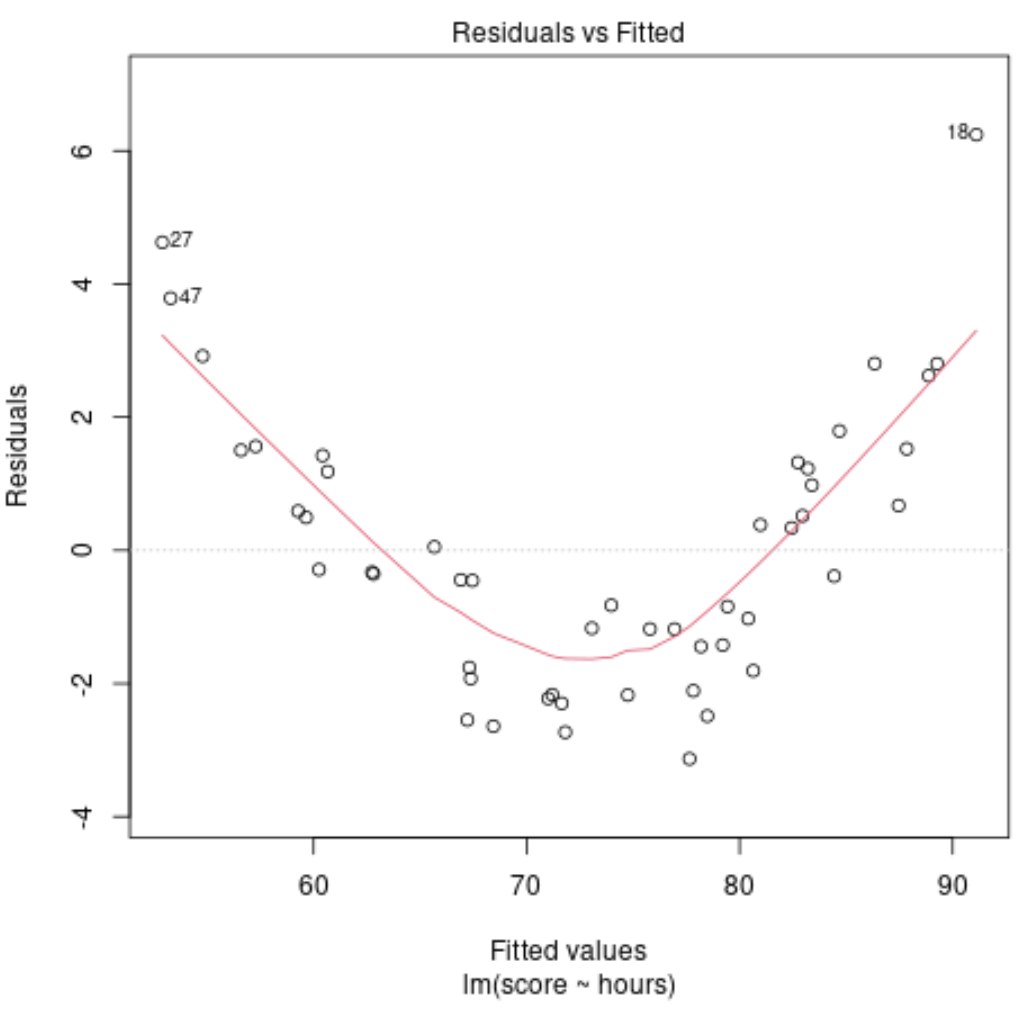
На графике мы видим, что в остатках наблюдается явная нелинейная закономерность – остатки имеют U-образную форму.

Это говорит нам о том, что линейная модель не подходит для этих конкретных данных и что вместо этого было бы разумно использовать модель полиномиальной регрессии.

3. Рассчитайте скорректированное значение R-квадрата модели.

Другой способ определить, следует ли вам использовать полиномиальную регрессию, — это подогнать как модель линейной регрессии, так и модель полиномиальной регрессии, и вычислить подобранные значения R-квадрата для обеих моделей.

Скорректированный R-квадрат представляет собой долю дисперсии переменной ответа, которую можно объяснить переменными-предикторами в модели, с поправкой на количество переменных-предикторов в модели.

Модель с наибольшим скорректированным R-квадратом представляет собой модель, которая лучше всего может использовать предикторную переменную (переменные) для объяснения изменений переменной отклика.

Дополнительные ресурсы

В следующих руководствах объясняется, как выполнить полиномиальную регрессию с использованием различного статистического программного обеспечения:

Введение в полиномиальную регрессию
Как выполнить полиномиальную регрессию в R
Как выполнить полиномиальную регрессию в Python
Как выполнить полиномиальную регрессию в Excel