Интерполяция или экстраполяция: в чем разница?

Два термина, которые студенты часто путают в статистике, — это интерполяция и экстраполяция .

Вот разница:

Интерполяция относится к прогнозированию значений, попадающих в диапазон точек данных.

Экстраполяция относится к прогнозированию значений, выходящих за пределы диапазона точек данных.

Следующий пример иллюстрирует разницу между этими двумя терминами.

Пример: интерполяция и экстраполяция

Предположим, у нас есть следующий набор данных:

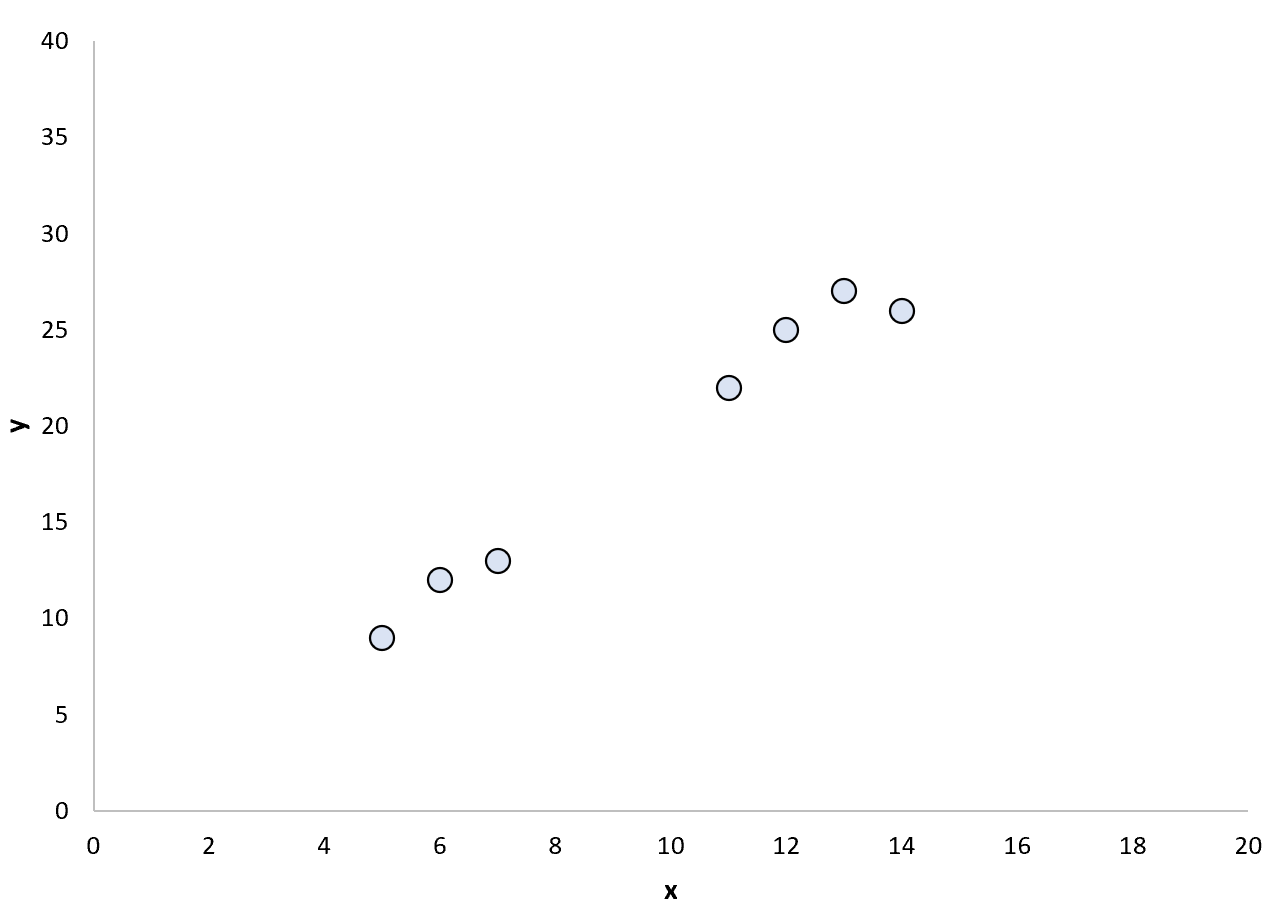
Мы можем решить подогнать к этим точкам простую модель линейной регрессии :

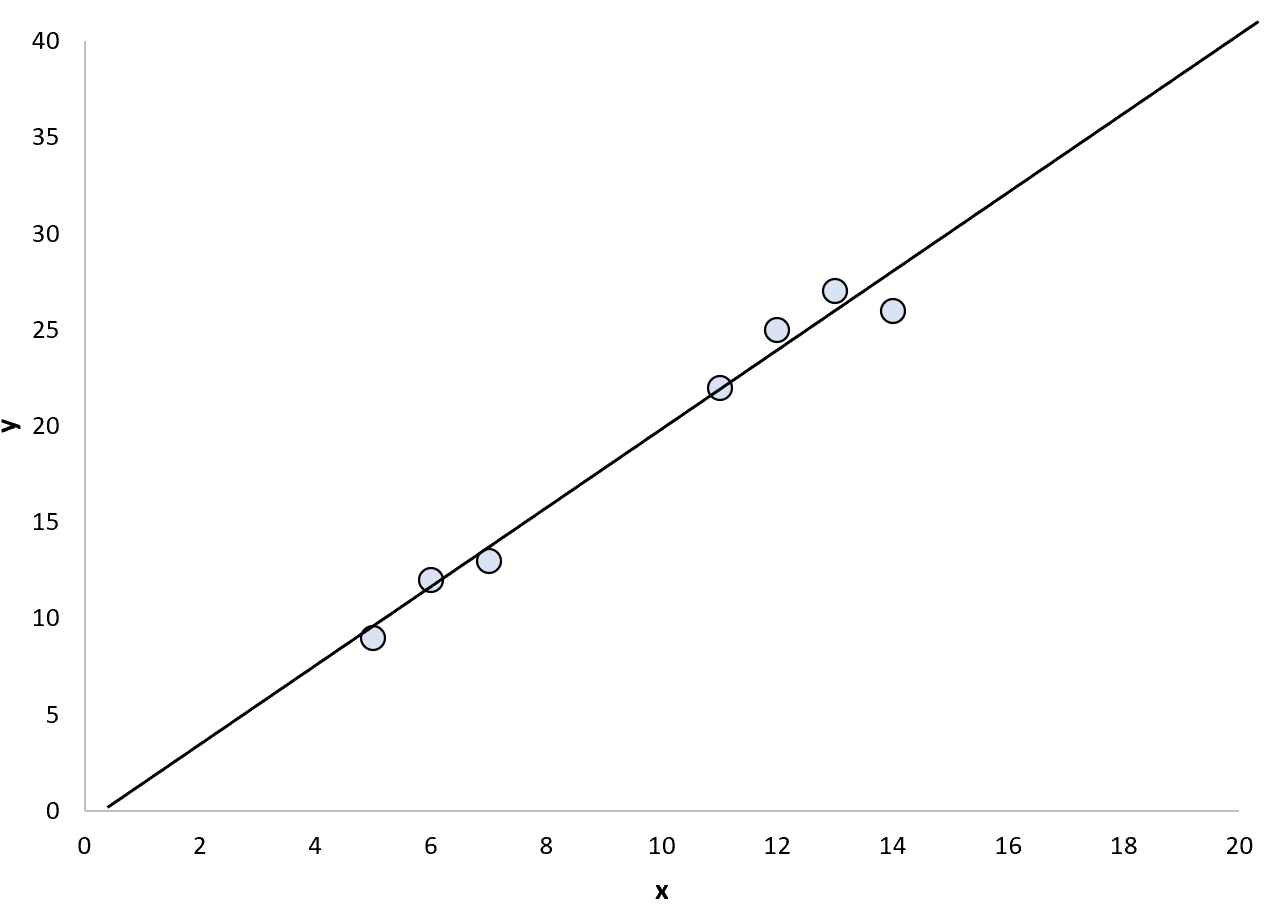
Затем мы могли бы использовать подобранную модель регрессии для прогнозирования значений точек как внутри , так и за пределами диапазона точек данных.

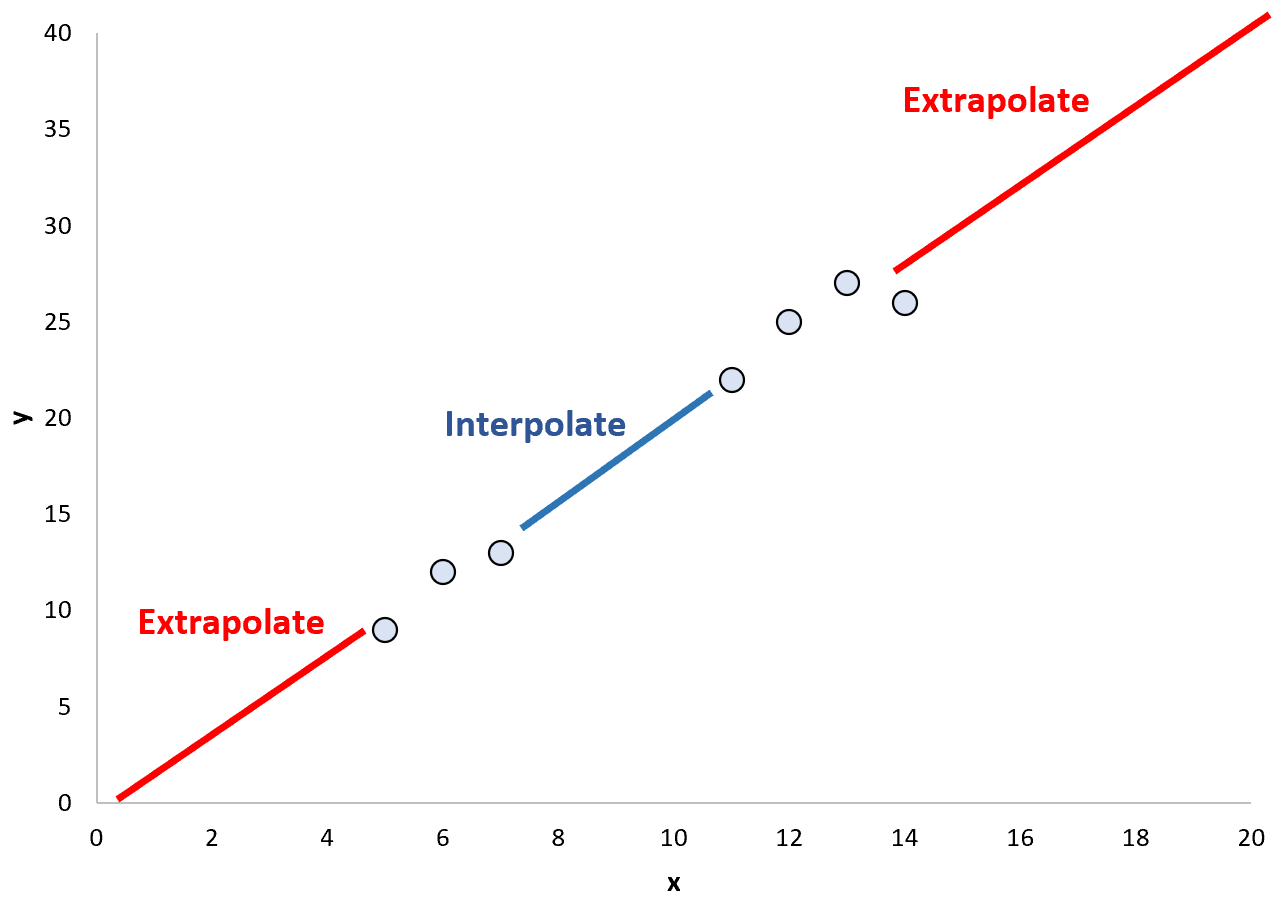
Когда мы используем подобранную модель регрессии для прогнозирования значений точек в существующем диапазоне точек данных, это называется интерполяцией.

И наоборот, когда мы используем подобранную модель регрессии для прогнозирования значений точек за пределами существующего диапазона, это называется экстраполяцией :

Потенциальная опасность экстраполяции

Когда мы экстраполируем, мы предполагаем, что та же самая закономерность, которая существует внутри текущего диапазона точек данных, также существует и за его пределами.

Однако это может быть опасным предположением, поскольку вполне возможно, что закономерность, существующая за пределами текущего диапазона точек данных, сильно отличается:

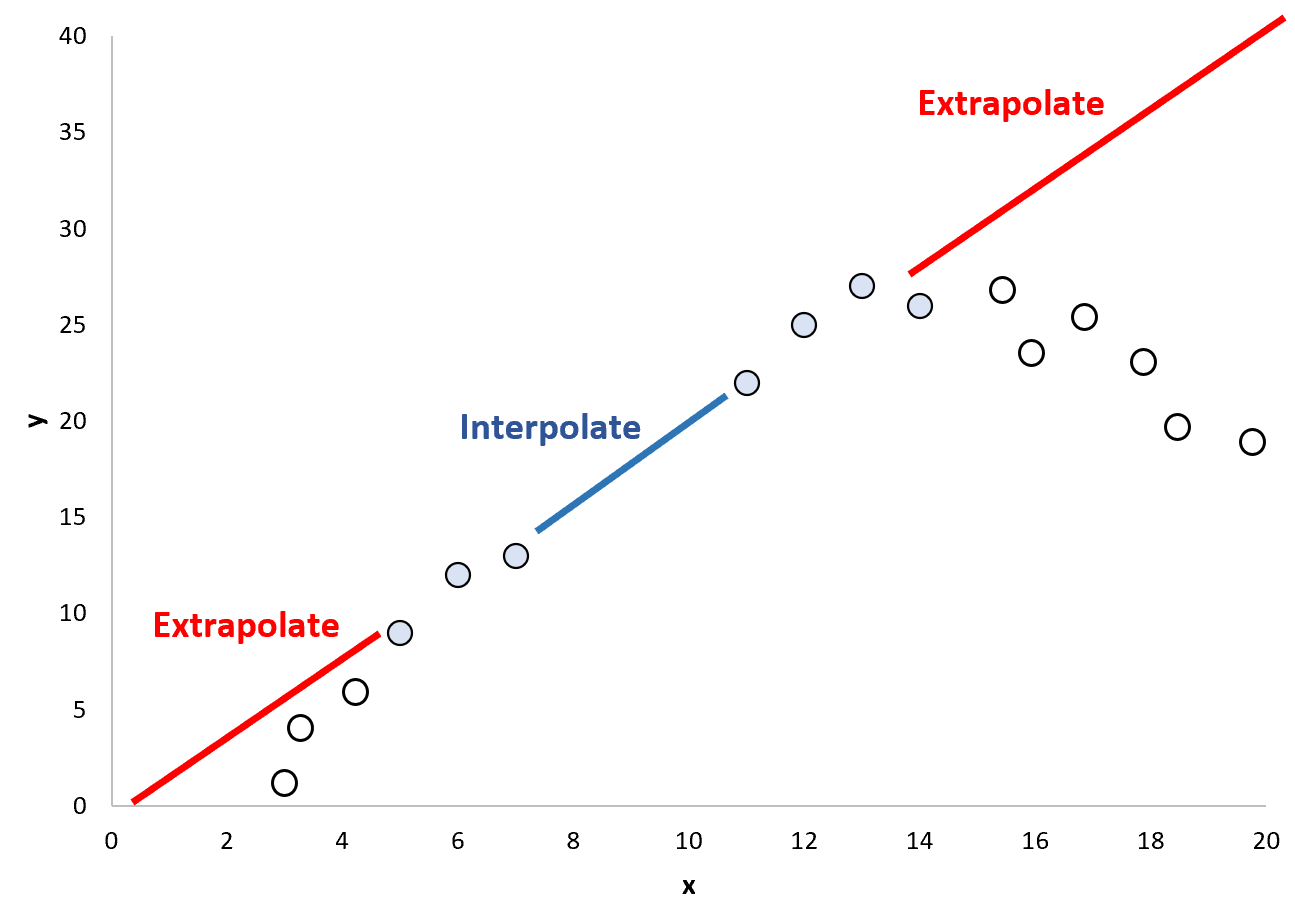
По этой причине может быть опасно использовать экстраполяцию для прогнозирования значений точек данных, выходящих за пределы диапазона значений, использованных для создания модели регрессии.

На практике часто имеет смысл использовать экстраполяцию для прогнозирования значений точек, которые немного выходят за пределы диапазона существующих значений, но чем дальше от диапазона, тем больше вероятность того, что разница между прогнозируемым значением и фактическим значением ценность важна. .

Когда использовать экстраполяцию

Часто требуется знание конкретной предметной области, чтобы определить, является ли экстраполяция разумной идеей или нет.

Например, предположим, что отдел маркетинга компании применяет простую модель линейной регрессии, используя расходы на рекламу в качестве предикторной переменной и общий доход в качестве переменной отклика.

В этом сценарии разумно предположить, что устойчивое увеличение расходов на рекламу приведет к предсказуемому увеличению общего дохода:

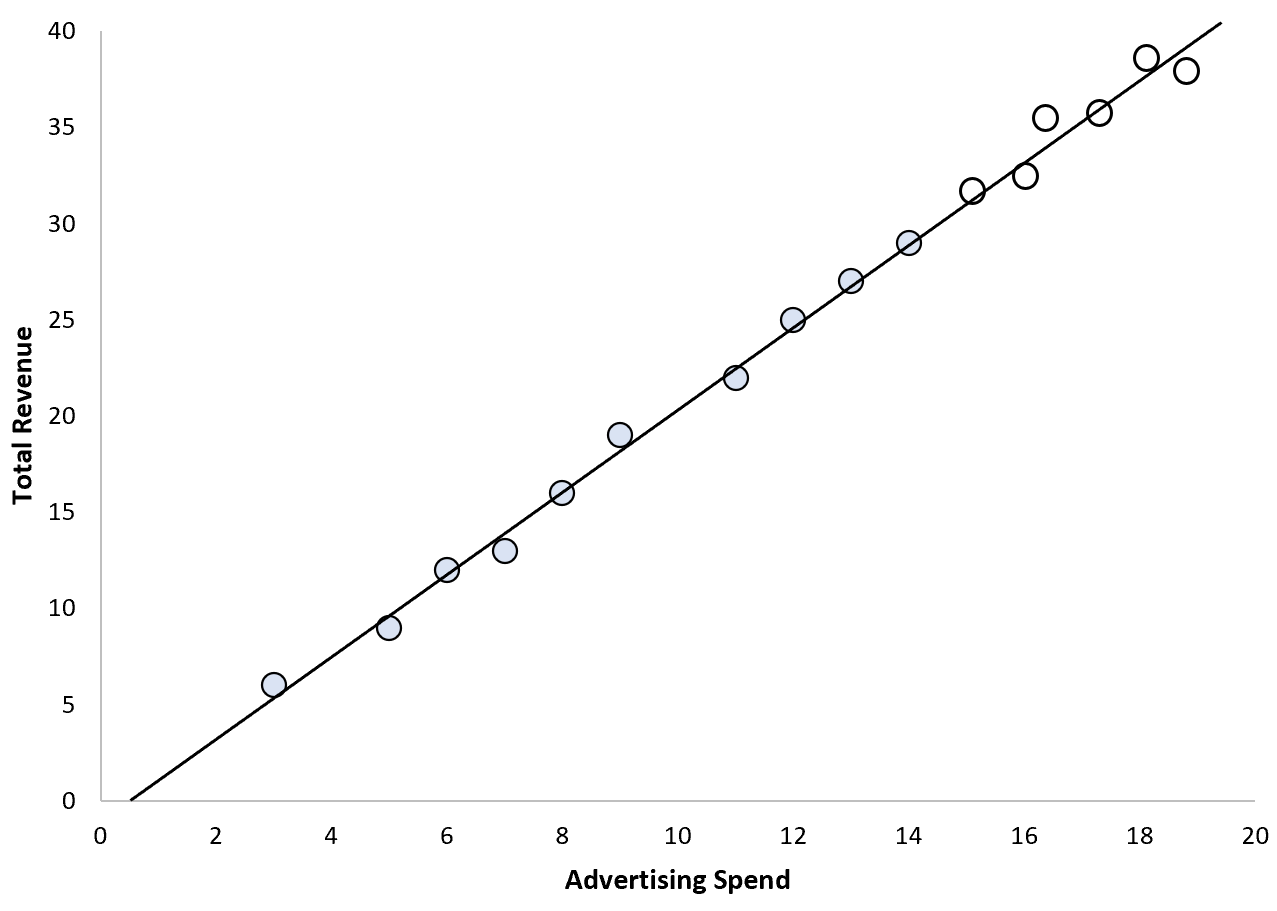
В этом сценарии мы можем быть вполне уверены в своей способности экстраполировать значения.

Однако рассмотрим сценарий, в котором биолог хочет использовать общее количество удобрений для прогнозирования роста растений.

Она может решить подогнать к точкам данных простую модель линейной регрессии, но поскольку существует верхний предел высоты растения, вероятно, не имеет смысла использовать экстраполяцию для прогнозирования значений точек. вне диапазона значений. значения, используемые для соответствия модели:

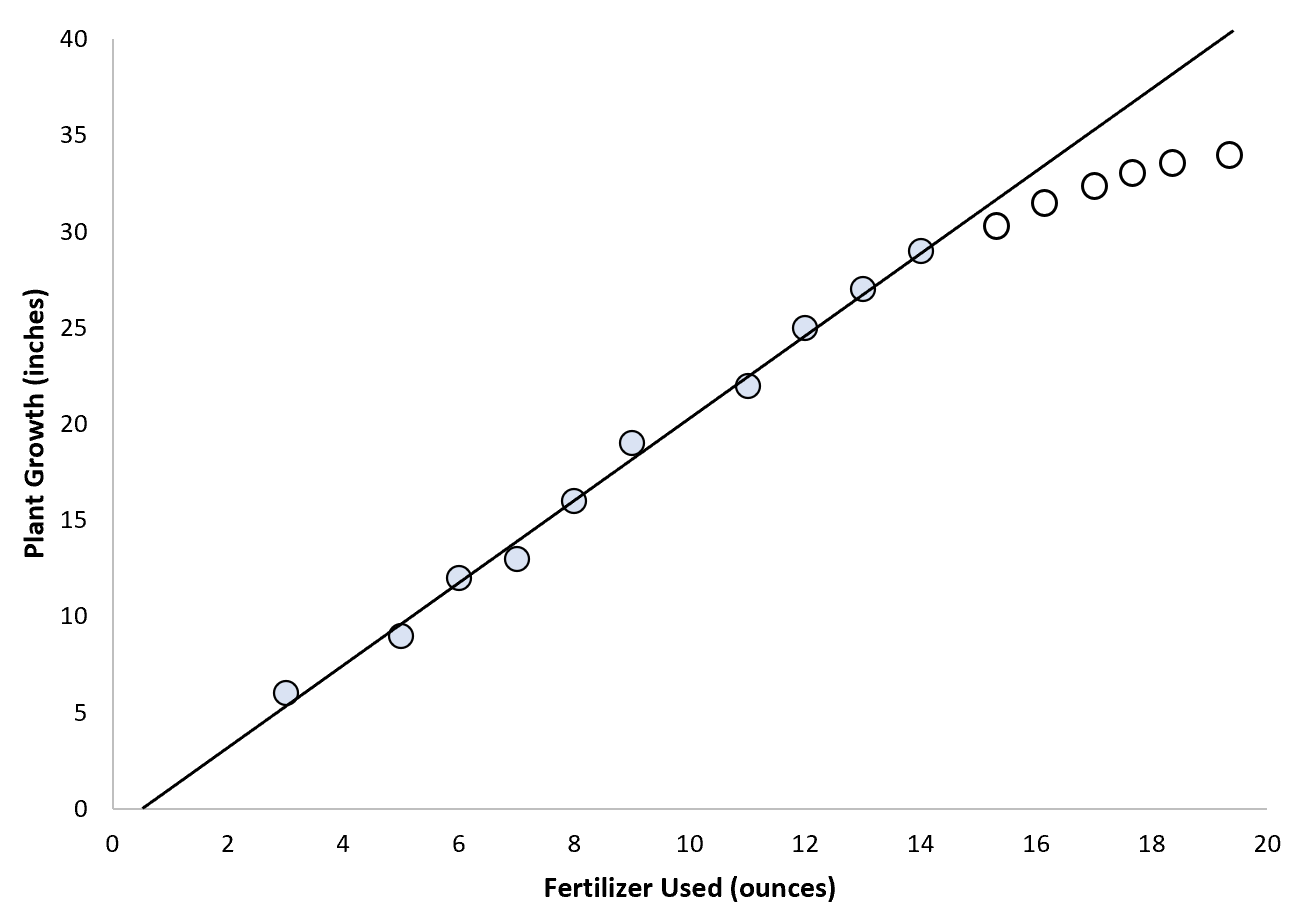
В этом сценарии у нас может быть гораздо меньше уверенности в нашей способности экстраполировать значения.

Вывод : в некоторых областях экстраполяция может иметь больше смысла, чем в других, но всегда существует потенциальная опасность того, что модель, существующая в диапазоне значений, используемых для соответствия модели, не существует за пределами пляжа.

Дополнительные ресурсы

Как выполнить линейную интерполяцию в Excel
Как делать прогнозы с помощью линейной регрессии