Гамма-распределение

К бенджамин андерсон 3 августа, 2023 Вероятность 0 комментариев

В этой статье объясняется, что такое гамма-распределение и для чего оно используется. Таким образом, вы найдете определение гамма-распределения, его свойства и то, как выглядит его графическое представление.

Что такое гамма-распределение?

Гамма-распределение представляет собой непрерывное распределение вероятностей, определяемое двумя характерными параметрами: α и λ. Другими словами, гамма-распределение зависит от значения двух его параметров: α — параметра формы и λ — параметра масштаба.

Символом гамма-распределения является заглавная греческая буква Γ. Итак, если случайная величина подчиняется гамма-распределению, она записывается следующим образом:

$X\sim \Gamma(\alpha,\lambda)$

Гамма-распределение также можно параметризовать с помощью параметра формы k = α и обратного параметра масштаба θ = 1/λ. Во всех случаях два параметра, определяющие гамма-распределение, являются положительными действительными числами.

Обычно гамма-распределение используется для моделирования наборов данных с перекосом вправо, чтобы в левой части графика была большая концентрация данных. Например, гамма-распределение используется для моделирования надежности электрических компонентов.

Диаграмма распределения гамма-излучения

График гамма-распределения зависит от значений его характерных параметров. Ниже вы можете увидеть, как меняется функция плотности гамма-распределения в зависимости от параметра формы и параметра масштаба.

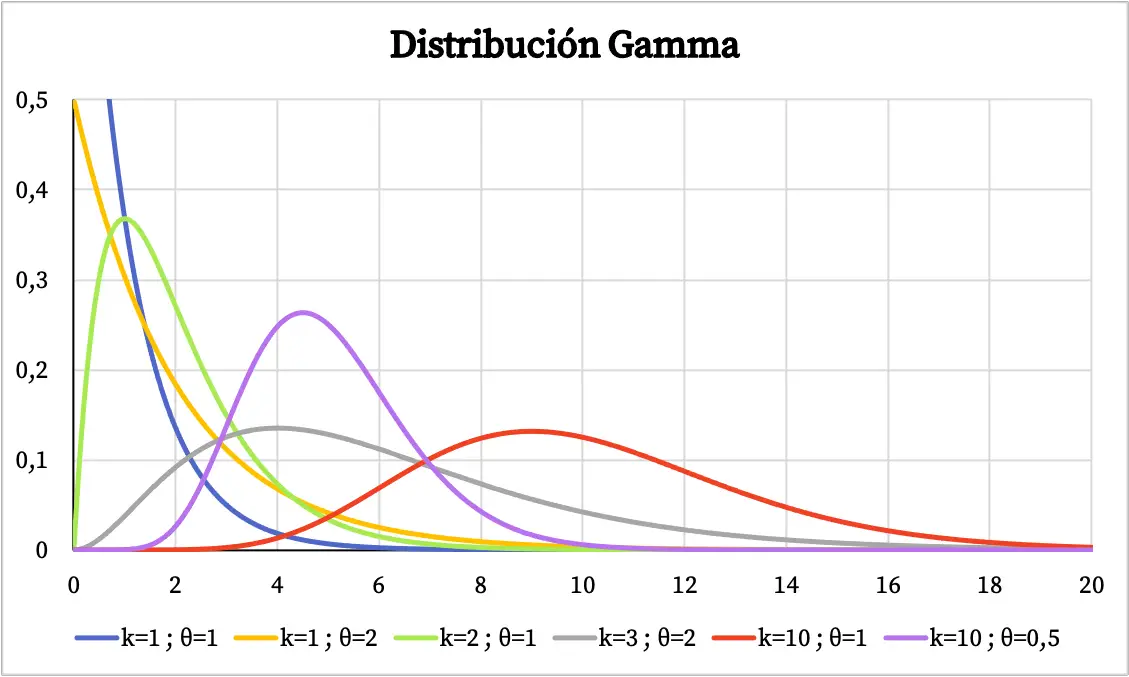
С другой стороны, вы можете увидеть график кумулятивной функции вероятности гамма-распределения ниже:

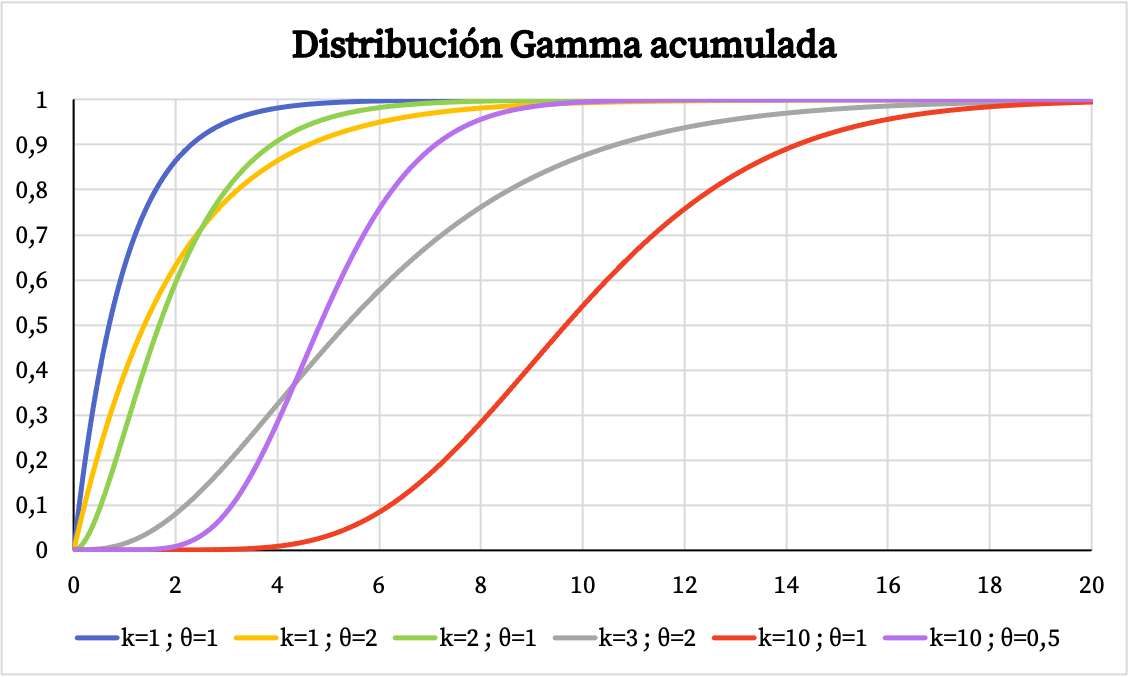
график кумулятивной функции вероятности распределения Гамма

Характеристики гамма-распределения

Затем мы увидим, каковы характеристики гамма-распределения.

График гамма-распределения полностью определяется двумя его характерными параметрами: α — параметр формы и λ — параметр масштаба.

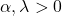
$\alpha , \lambda >0″ title=»Rendered by QuickLaTeX.com» height=»16″ width=»62″ style=»vertical-align: -4px;»></p> </p> <ul> <li> Область гамма-распределения состоит только из положительных чисел.</li> </ul> <p class=$ $x\in (0,+\infty)$

Среднее значение гамма-распределения равно отношению параметра формы к параметру масштаба, т.е. α/λ.

$E[X]=\cfrac{\alpha}{\lambda}$

Дисперсия гамма-распределения эквивалентна параметру формы, деленному на квадрат параметра масштаба.

$Var(X)=\cfrac{\alpha}{\lambda^2}$

Для значений α меньше 1 мода равна 0. Но если α равно или больше 1, моду гамма-распределения можно рассчитать по следующей формуле:

$\begin{array}{c}Mo=0 \qquad \text{para } \alpha<1\\[2ex]Mo=\cfrac{\alpha-1}{\lambda} \qquad \text{para } \alpha\geq1\end{array}$

Формула функции плотности гамма-распределения:

$\displaystyle f(x)=\frac{\lambda(\lambda x)^{\alpha-1}e^{-\lambda x}}{\Gamma(\alpha)}$

Где Γ — гамма-функция, которая определяется как:

$\displaystyle \Gamma(\alpha)=\int_0^\infty t^{\alpha-1}e^{-t}dt$

Формула кумулятивного распределения случайной величины, определяемой гамма-распределением, выглядит следующим образом:

$\displaystyle F(x)=\int_0^x\frac{\lambda(\lambda y)^{\alpha-1}e^{-\lambda y}}{\Gamma(\alpha)}\;dy$

Если параметр формы α равен 1, то гамма-распределение эквивалентно экспоненциальному распределению с тем же масштабным параметром λ.

$X\sim \Gamma(1,\lambda) \ \color{orange}\bm{\longrightarrow}\color{black} \ X\sim \text{Exp}(\lambda)$

Когда параметр масштаба λ является средним, тогда гамма-распределение является частным случаем распределения хи-квадрат .

$\displaystyle X\sim \Gamma\left(\frac{n}{2},\frac{1}{2}\right) \text{con } n\in \mathbb{N}\ \color{orange}\bm{\longrightarrow}\color{black} \ X\sim \chi_n^2$

Об авторе

бенджамин андерсон

Здравствуйте, я Бенджамин, профессор статистики на пенсии, ставший преданным преподавателем Statorials. Имея обширный опыт и знания в области статистики, я хочу поделиться своими знаниями, чтобы расширить возможности студентов с помощью Statorials. Узнать больше

Что такое гамма-распределение?

Диаграмма распределения гамма-излучения

Характеристики гамма-распределения

Об авторе

бенджамин андерсон

Добавить комментарий