Как преобразовать данные в python (журнал, квадратный корень, кубический корень)
Многие статистические тесты предполагают, что наборы данных распределены нормально. Однако на практике это часто не так.
Один из способов решения этой проблемы — преобразовать распределение значений в наборе данных с помощью одного из трёх преобразований:
1. Преобразование журнала: преобразуйте переменную ответа из y в log(y) .
2. Преобразование квадратного корня: преобразуйте переменную ответа из y в √y .
3. Преобразование корня куба: преобразуйте переменную ответа из y в y 1/3 .
Выполняя эти преобразования, набор данных обычно становится более нормально распределенным.
Следующие примеры показывают, как выполнить эти преобразования в Python.
Преобразование журнала в Python
Следующий код показывает, как выполнить логарифмическое преобразование переменной и создать параллельные графики для отображения исходного распределения и распределения данных с логарифмическим преобразованием:
import numpy as np import matplotlib. pyplot as plt #make this example reproducible n.p. random . seeds (0) #create beta distributed random variable with 200 values data = np. random . beta (a= 4 , b= 15 , size= 300 ) #create log-transformed data data_log = np. log (data) #define grid of plots fig, axs = plt. subplots (nrows= 1 , ncols= 2 ) #create histograms axs[0]. hist (data, edgecolor=' black ') axs[1]. hist (data_log, edgecolor=' black ') #add title to each histogram axs[0]. set_title (' Original Data ') axs[1].set_title(' Log-Transformed Data ')
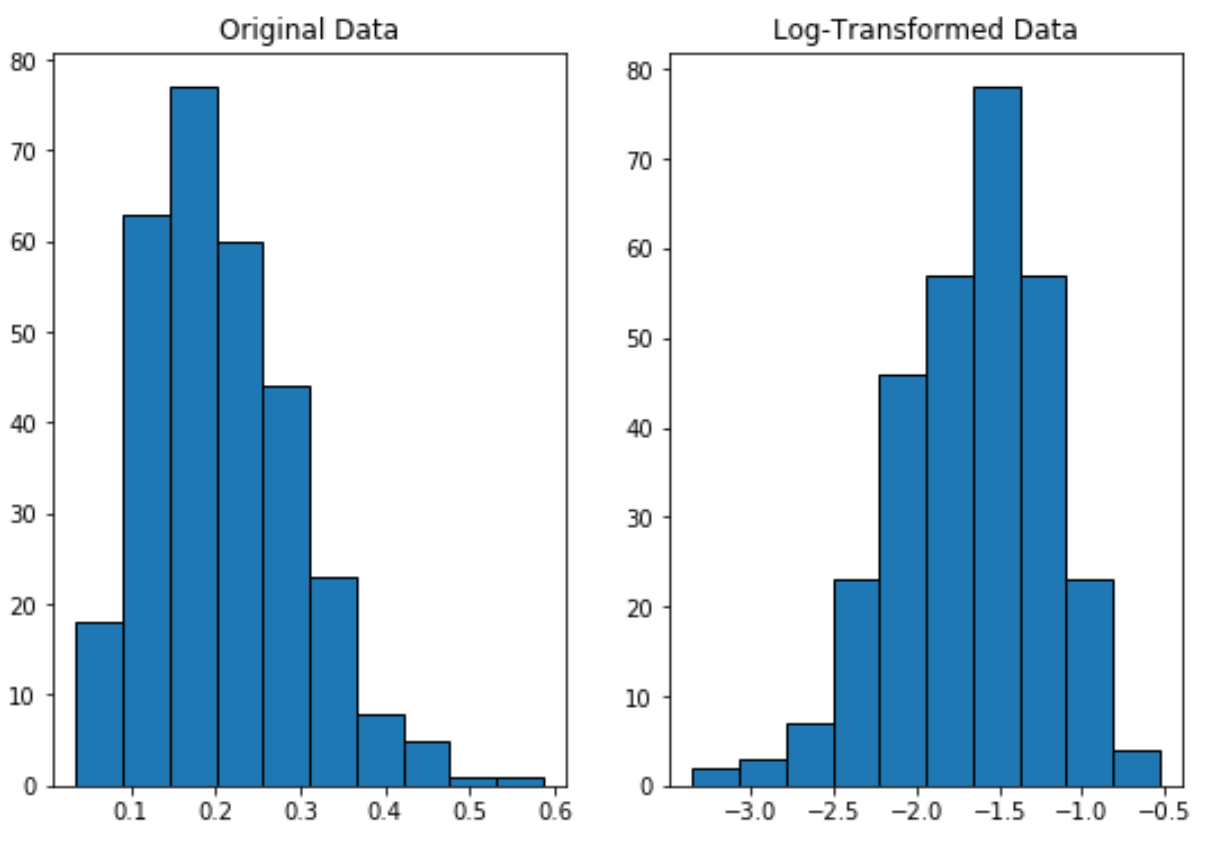
Обратите внимание, что распределение с логарифмическим преобразованием распределяется более нормально, чем исходное распределение.
Это все еще не идеальная «форма колокола», но она ближе к нормальному распределению, чем к исходному распределению.
Преобразование квадратного корня в Python
В следующем коде показано, как выполнить преобразование квадратного корня переменной и создать параллельные графики для отображения исходного распределения и распределения данных, преобразованного квадратным корнем:
import numpy as np import matplotlib. pyplot as plt #make this example reproducible n.p. random . seeds (0) #create beta distributed random variable with 200 values data = np. random . beta (a= 1 , b= 5 , size= 300 ) #create log-transformed data data_log = np. sqrt (data) #define grid of plots fig, axs = plt. subplots (nrows= 1 , ncols= 2 ) #create histograms axs[0]. hist (data, edgecolor=' black ') axs[1]. hist (data_log, edgecolor=' black ') #add title to each histogram axs[0]. set_title (' Original Data ') axs[1].set_title(' Square Root Transformed Data ')
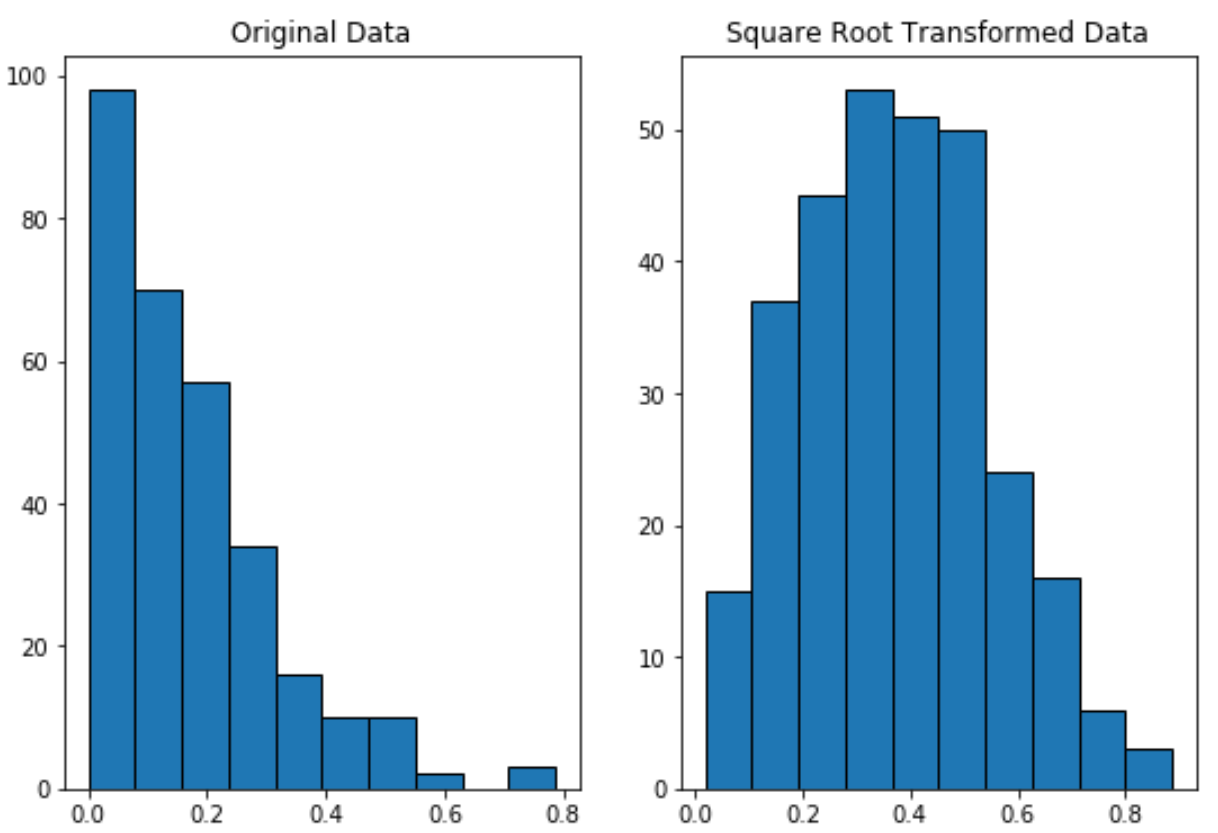
Обратите внимание, что данные, преобразованные квадратным корнем, распределяются гораздо более нормально, чем исходные данные.
Преобразование корня куба в Python
В следующем коде показано, как выполнить преобразование кубического корня переменной и создать параллельные графики для отображения исходного распределения и распределения данных, преобразованного кубическим корнем:
import numpy as np import matplotlib. pyplot as plt #make this example reproducible n.p. random . seeds (0) #create beta distributed random variable with 200 values data = np. random . beta (a= 1 , b= 5 , size= 300 ) #create log-transformed data data_log = np. cbrt (data) #define grid of plots fig, axs = plt. subplots (nrows= 1 , ncols= 2 ) #create histograms axs[0]. hist (data, edgecolor=' black ') axs[1]. hist (data_log, edgecolor=' black ') #add title to each histogram axs[0]. set_title (' Original Data ') axs[1].set_title(' Cube Root Transformed Data ')
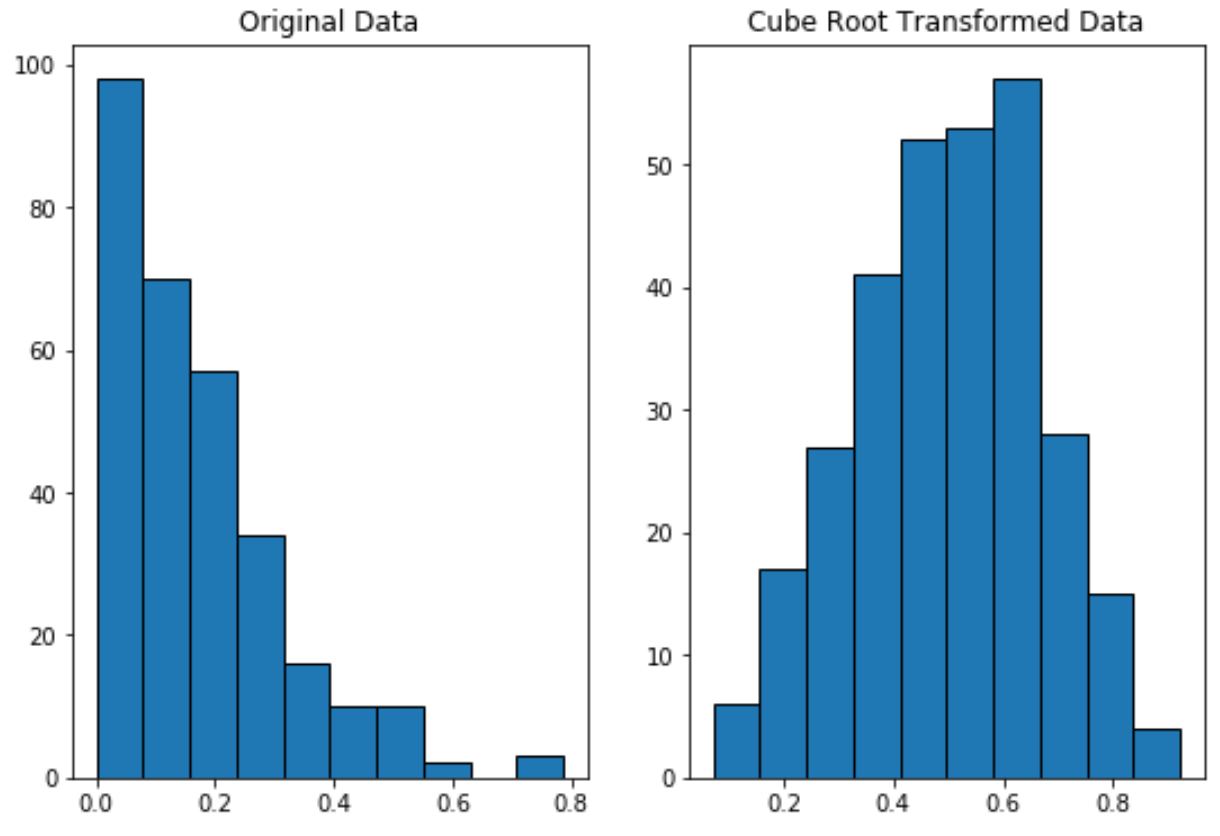
Обратите внимание, что данные, преобразованные в корень куба, распределяются гораздо более нормально, чем исходные данные.
Дополнительные ресурсы
Как рассчитать Z-оценки в Python
Как нормализовать данные в Python
Что такое предположение нормальности в статистике?