Распределение вейбулла

К бенджамин андерсон 3 августа, 2023 Вероятность 0 комментариев

В этой статье объясняется, что такое распределение Вейбулла и для чего оно используется. Кроме того, вы сможете увидеть графическое представление распределения Вейбулла и свойства этого типа распределения вероятностей.

Что такое распределение Вейбулла?

Распределение Вейбулла представляет собой непрерывное распределение вероятностей, определяемое двумя характеристическими параметрами: параметром формы α и параметром масштаба λ.

В статистике распределение Вейбулла в основном используется для анализа выживаемости. Аналогично, распределение Вейбулла имеет множество приложений в различных областях. Ниже мы подробно рассмотрим использование распределения Вейбулла.

$X\sim\text{Weibull}(\alpha,\lambda)$

По мнению авторов, распределение Вейбулла также можно параметризовать тремя параметрами. Затем добавляется третий параметр, называемый пороговым значением, который указывает абсциссу, с которой начинается график распределения.

Распределение Вейбулла названо в честь шведа Валодди Вейбулла, который подробно описал его в 1951 году. Однако распределение Вейбулла было открыто Морисом Фреше в 1927 году и впервые применено Розином и Раммлером в 1933 году.

Построение распределения Вейбулла

Увидев определение распределения Вейбулла, мы увидим, как меняется его графическое представление в зависимости от значений его параметров.

Ниже вы можете увидеть несколько примеров того, как график функции плотности распределения Вейбулла меняется в зависимости от значения параметра формы и параметра масштаба.

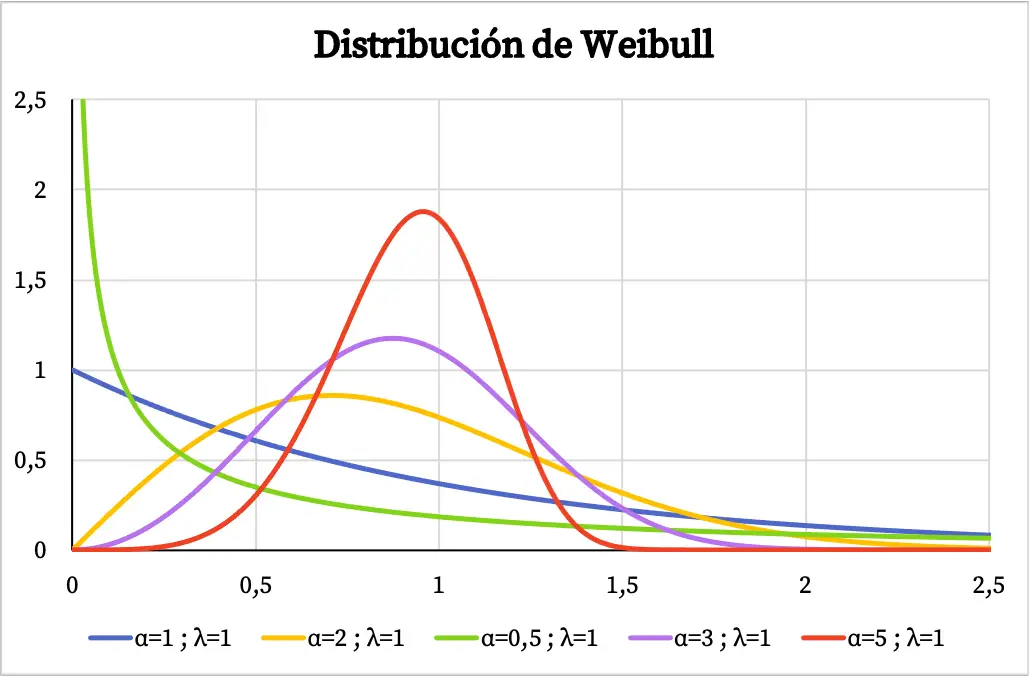
Когда распределение Вейбулла используется для моделирования интенсивности отказов системы как функции времени, значение параметра формы α означает следующее:

α<1: интенсивность отказов со временем снижается.
α=1: интенсивность отказов постоянна во времени.
α>1: интенсивность отказов со временем увеличивается.

С другой стороны, на следующем графике вы можете увидеть кумулятивную функцию вероятности распределения Вейбулла, построенную на основе его характеристических значений.

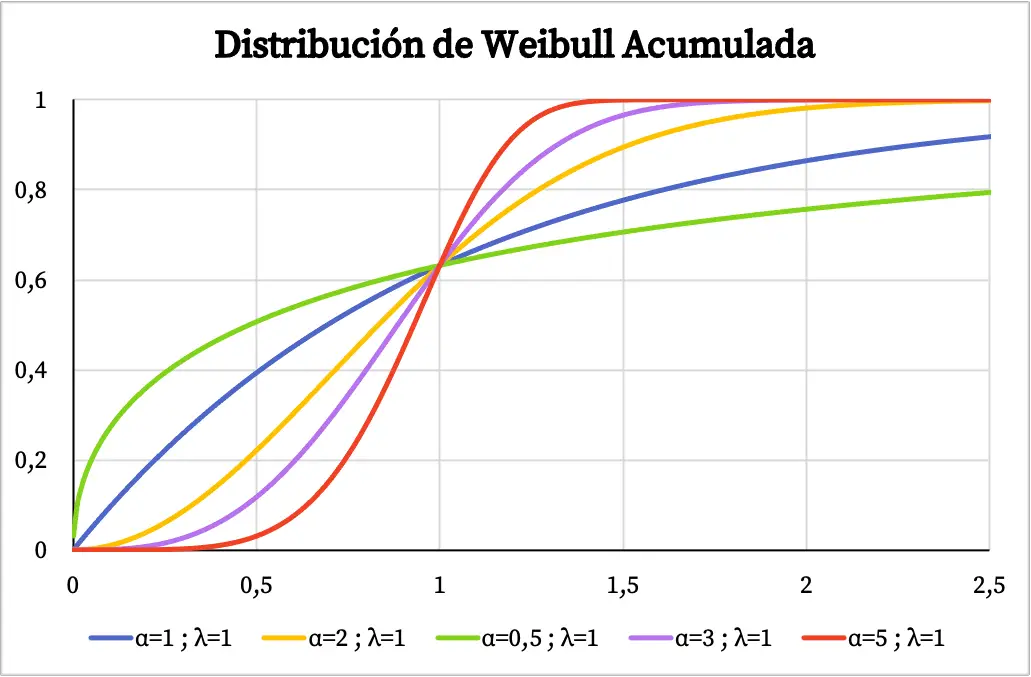
кумулятивная вероятность распределения Вейбулла

Характеристики распределения Вейбулла

Распределение Вейбулла имеет следующие характеристики:

Распределение Вейбулла имеет два характерных параметра, которые определяют его график: параметр формы α и параметр масштаба λ. Оба параметра являются положительными действительными числами.

$\begin{array}{c}\alpha >0\\[2ex]\lambda >0\\[2ex]\text{Weibull}(\alpha,\lambda)\end{array}» title=»Rendered by QuickLaTeX.com» height=»92″ width=»101″ style=»vertical-align: 0px;»></p> </p> <ul> <li> Распределение Вейбулла принимает только положительные значения абсцисс.</li> </ul> <p class=$ $x\in (0,+\infty)$

Среднее значение распределения Вейбулла рассчитывается по следующей формуле:

$\displaystyle E[X]=\frac{1}{\lambda}\;\Gamma\left(1+\frac{1}{\alpha}\right)$

С другой стороны, формула для нахождения дисперсии распределения Вейбулла:

$\displaystyle Var(X)=\frac{1}{\lambda^2}\left[\Gamma\left(1+\frac{2}{\alpha}\right)-\Gamma^2\left(1+\frac{1}{\alpha}\right)\right]$

Режим случайной величины, которая соответствует распределению Вейбулла с α>1, можно определить с помощью следующего выражения:

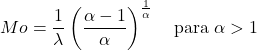
$\displaystyle Mo=\frac{1}{\lambda}\left(\frac{\alpha-1}{\alpha} \right)^{\frac{1}{\alpha}} \quad \text{para } \alpha>1″ title=»Rendered by QuickLaTeX.com» height=»50″ width=»257″ style=»vertical-align: -17px;»></p> </p> <ul> <li> Формула функции плотности распределения Вейбулла:</li> </ul> <p class=$ $\displaystyle P[X=x]=\lambda\alpha(\lambda x)^{\alpha-1}e^{-(\lambda x)^\alpha}$

Аналогично, формула для кумулятивной функции вероятности распределения Вейбулла имеет вид:

$\displaystyle P[X\leq x]=1- e^{-(\lambda x)^\alpha}$

Коэффициент асимметрии распределения Вейбулла рассчитывается по следующей формуле:

$\displaystyle A=\frac{\displaystyle\Gamma\left(1+\frac{3}{\alpha}\right)\frac{|}{\lambda^3}-3\mu\sigma^2-\mu^3}{\sigma^3}$

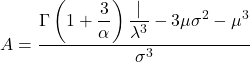
Наконец, формула, позволяющая определить коэффициент эксцесса распределения Вейбулла, имеет следующий вид:

$\displaystyle C=\frac{\displaystyle\frac{1}{\lambda^4}\Gamma \left(1+\frac{4}{\alpha}\right)-4\gamma_{1}\sigma^3\mu-6\mu^2\sigma^2-\mu^4}{\sigma^4}$

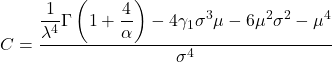
Золото

$\Gamma_i=\Gamma\left(1+\frac{i}{\alpha}\right).$

Применение распределения Вейбулла

Распределение Вейбулла имеет множество приложений, в том числе:

В прикладной статистике распределение Вейбулла используется при анализе выживаемости.
В технике распределение Вейбулла используется для моделирования функций, связанных со временем производства.
В радиолокационных системах для имитации дисперсии принимаемого сигнала.
В страховом секторе для моделирования размера претензий.
Например, в метеорологии для моделирования частоты различных скоростей ветра.

Об авторе

бенджамин андерсон

Здравствуйте, я Бенджамин, профессор статистики на пенсии, ставший преданным преподавателем Statorials. Имея обширный опыт и знания в области статистики, я хочу поделиться своими знаниями, чтобы расширить возможности студентов с помощью Statorials. Узнать больше