Означает ли причинно-следственная связь корреляцию? (3 примера)
Хорошо известно, что корреляция не предполагает причинно-следственной связи .
В качестве простого примера: если бы мы каждый год собирали данные об общем количестве выпускников средних школ и общем потреблении пиццы в Соединенных Штатах, мы бы обнаружили, что эти две переменные сильно коррелируют:
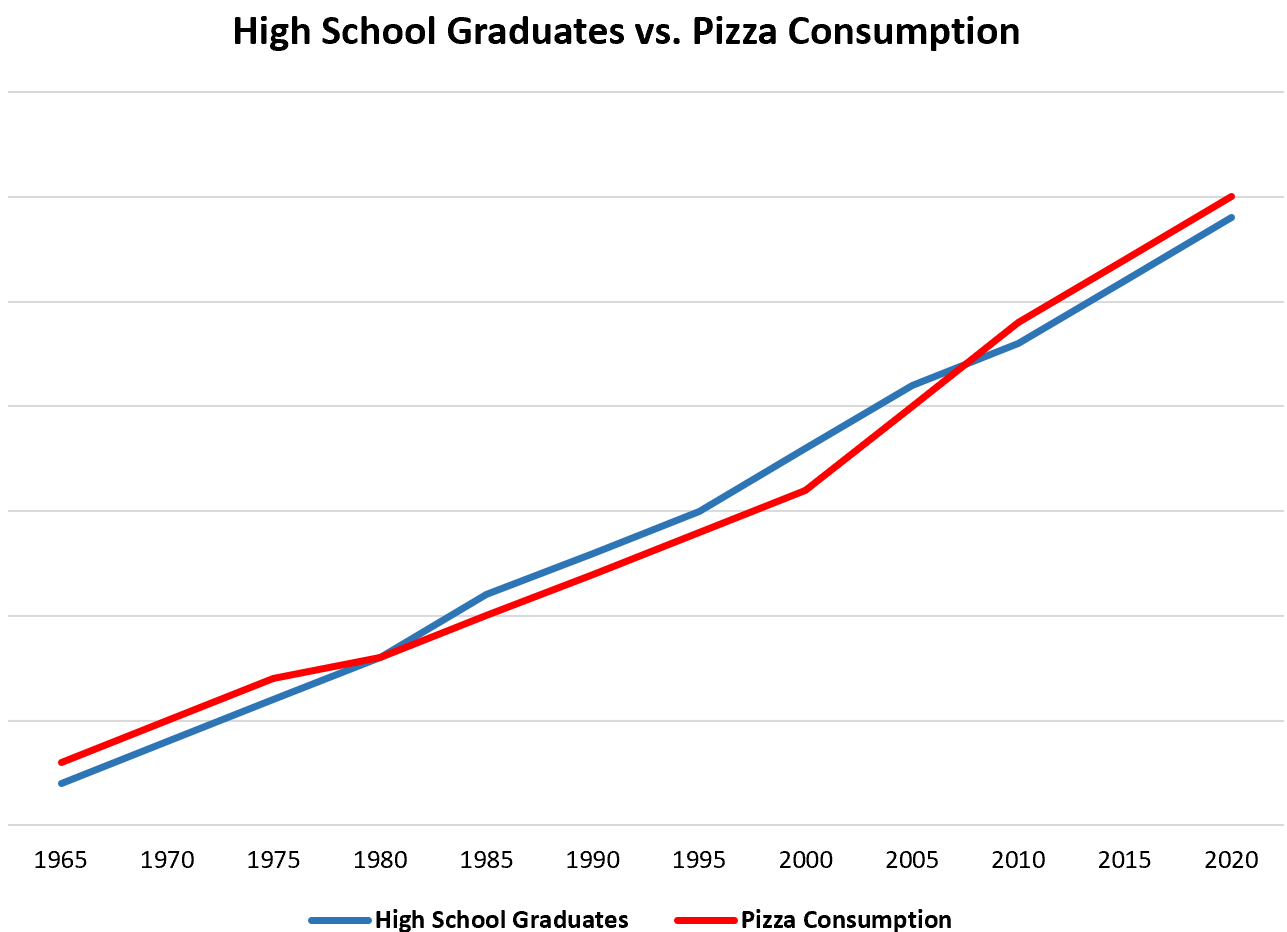
Это не означает, что увеличение числа выпускников школ приводит к увеличению потребления пиццы.
Наиболее вероятное объяснение состоит в том, что население США со временем увеличилось, а это означает, что число людей с дипломом средней школы и общее количество потребляемой пиццы увеличивается по мере увеличения населения.
А как насчет противоположного утверждения: предполагает ли причинно-следственная связь корреляцию?
Если одна переменная вызывает другую переменную, обязательно ли это означает, что эти две переменные будут коррелировать?
Краткий ответ: Нет.
Следующие примеры показывают, почему.
Пример 1: квадратичная зависимость
Предположим, что переменная X заставляет переменную Y принимать значение, равное X 2 .
Например:
- Если X = -10, то Y = -10 2 = 100
- Если X = 0, то Y = 0 2 = 0
- Если X = 10, то Y = 10 2 = 100
И так далее.
Если мы построим график зависимости между X и Y, это будет выглядеть так:
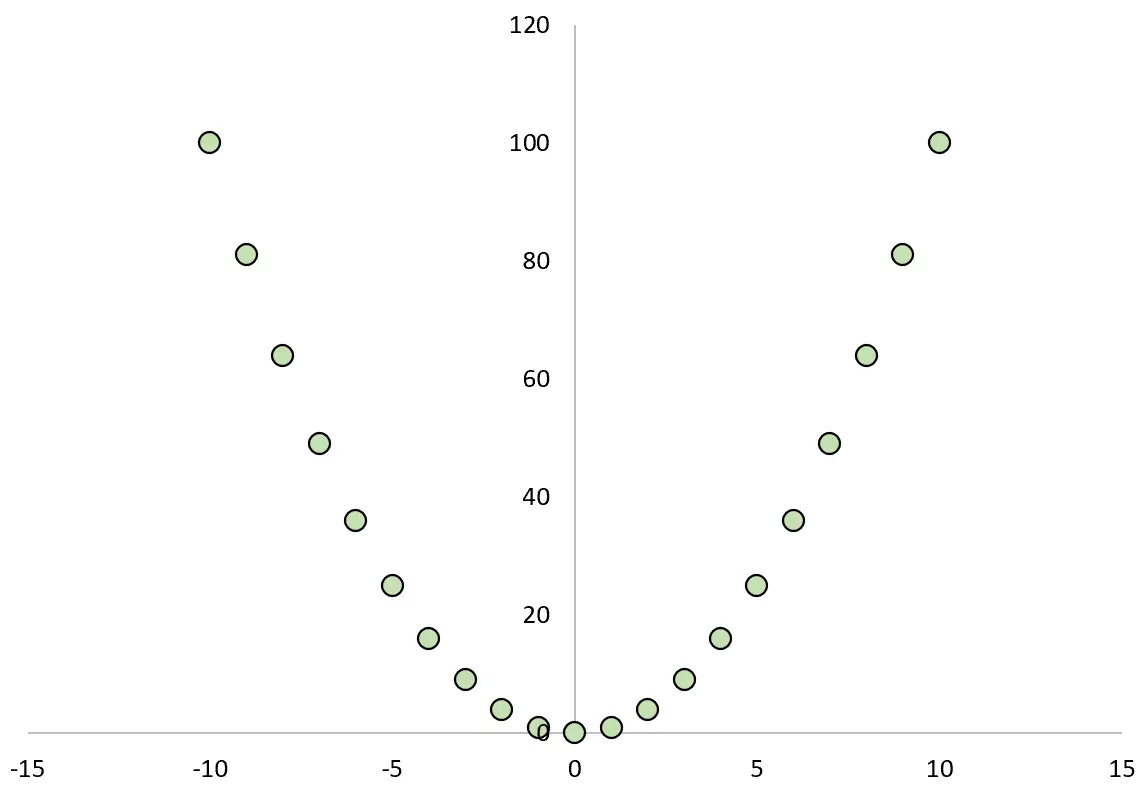
Если бы мы вычислили коэффициент корреляции Пирсона между двумя переменными, мы бы обнаружили, что корреляция равна нулю .
Хотя X вызывает Y, линейная корреляция между двумя переменными равна нулю.
Пример 2: отношение четвертой степени
Предположим, что переменная X заставляет переменную Y принимать значение, равное X 4 .
Например:
- Если X = -10, то Y = -10 4 = 10 000
- Если X = 0, то Y = 0 4 = 0
- Если X = 10, то Y = 10 4 = 10 000
И так далее.
Если мы построим график зависимости между X и Y, это будет выглядеть так:
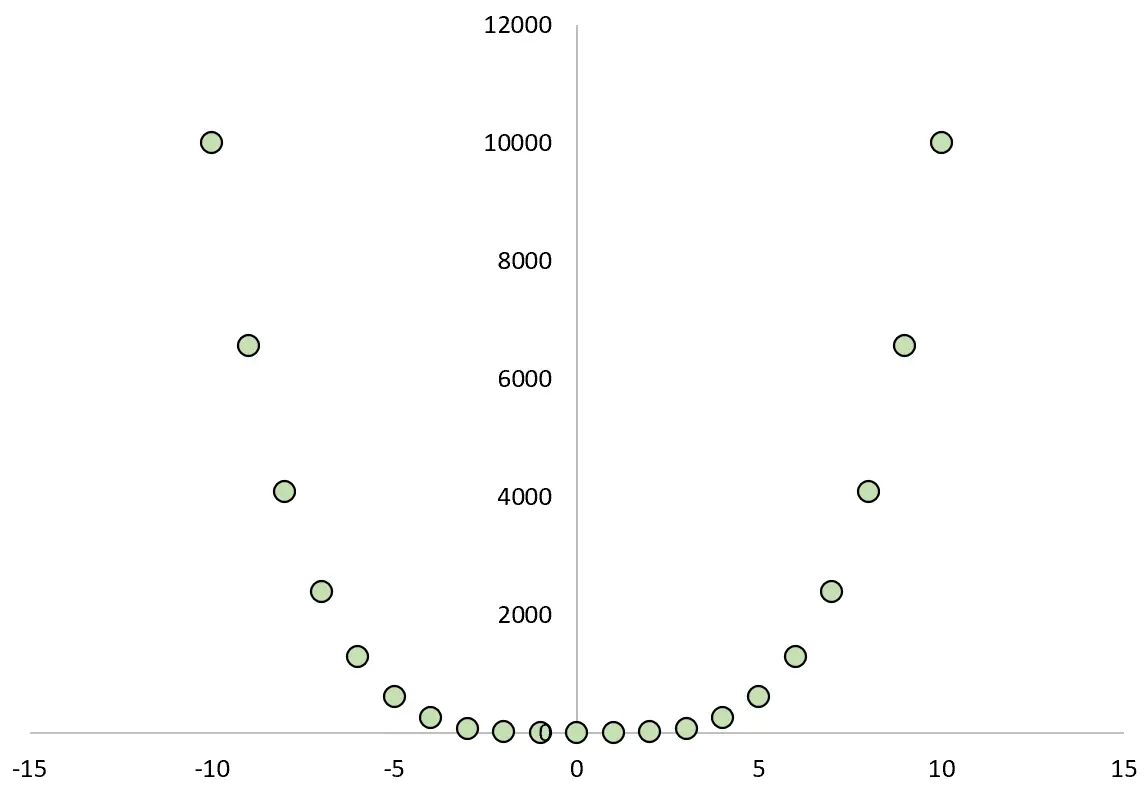
Если бы мы вычислили коэффициент корреляции Пирсона между двумя переменными, мы бы обнаружили, что корреляция равна нулю .
Мы знаем, что X вызывает Y, но линейная корреляция между двумя переменными равна нулю.
Пример 3: косинусное соотношение
Предположим, что переменная X заставляет переменную Y принимать значение, равное cos(X).
Например:
- Если X = -10, то Y = cos(-10) = -0,83907.
- Если X = 0, то Y = cos(0) = 1
- Если X = 10, то Y = cos(10) = -0,83907.
И так далее.
Если мы построим график зависимости между X и Y, это будет выглядеть так:
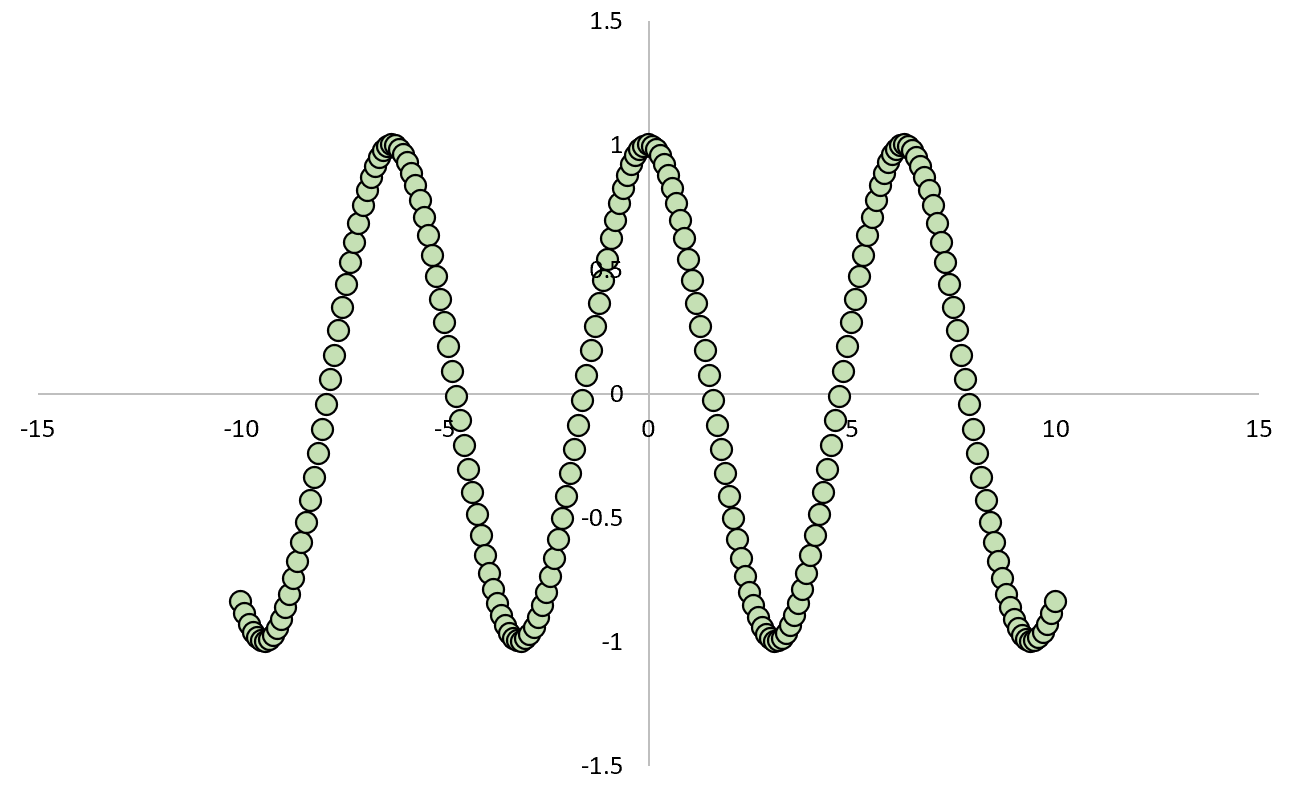
Если бы мы вычислили коэффициент корреляции Пирсона между двумя переменными, мы бы обнаружили, что корреляция равна нулю .
Мы знаем, что X вызывает Y, но линейная корреляция между двумя переменными равна нулю.
Дополнительные ресурсы
Следующие учебные пособия предоставляют дополнительную информацию о корреляции и причинно-следственной связи:
Корреляция не предполагает причинно-следственной связи: 5 конкретных примеров
Введение в коэффициент корреляции Пирсона
Обратная причинность: определение и примеры