Три предположения повторных измерений anova

ANOVA с повторными измерениями используется для определения того, существует ли статистически значимая разница между средними значениями трех или более групп, в которых одни и те же субъекты появляются в каждой группе.

Однако, прежде чем выполнять повторные измерения ANOVA, мы должны убедиться, что выполняются следующие предположения:

1. Независимость. Каждое наблюдение должно быть независимым.

2. Нормальность: распределение переменной ответа нормальное.

3. Сферичность: дисперсии различий между всеми комбинациями родственных групп должны быть равны.

Если одно или несколько из этих допущений нарушаются, результаты повторных измерений ANOVA могут оказаться ненадежными.

В этой статье мы даем объяснение каждому предположению, как определить, выполняется ли предположение и что делать, если оно не выполняется.

Гипотеза 1: Независимость

Повторные измерения ANOVA предполагают, что каждое наблюдение в вашем наборе данных не зависит от всех других наблюдений.

Как определить, выполняется ли это предположение

Самый простой способ проверить это предположение — убедиться, что каждый человек в наборе данных был случайным образом выбран из совокупности с использованием метода случайной выборки .

Если использовался метод случайной выборки, каждое наблюдение можно считать независимым.

Что делать, если это предположение не соблюдается

Если это предположение не выполняется, то это серьезная проблема, поскольку ценности каждого человека могут быть так или иначе связаны друг с другом.

Часто единственным выходом в этом случае является набор людей для нового исследования методом случайной выборки.

Гипотеза 2: нормальность

Повторные измерения ANOVA предполагают, что распределение переменной ответа является нормально распределенным .

Как определить, выполняется ли это предположение

Есть два способа проверить, верна ли эта гипотеза:

1. Создайте гистограмму или график QQ.

Вы можете визуально проверить, является ли распределение переменной ответа примерно нормальным, создав гистограмму или график QQ.

Если вы создаете гистограмму , просто проверьте, что распределение переменной отклика примерно соответствует форме «колокола». Если это так, то часто можно предположить, что предположение о нормальности выполнено:

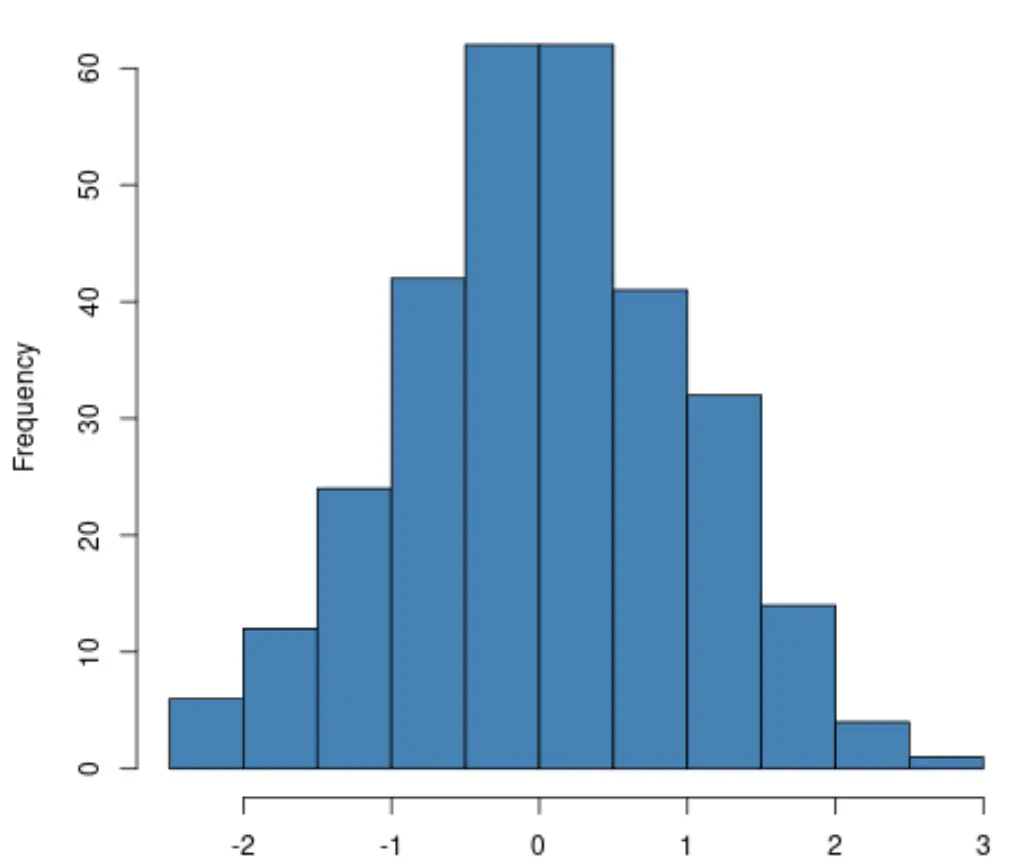
Если вы создаете график QQ , проверьте, лежат ли точки данных вдоль прямой диагональной линии. Если это так, то в целом можно предположить, что предположение о нормальности выполнено:

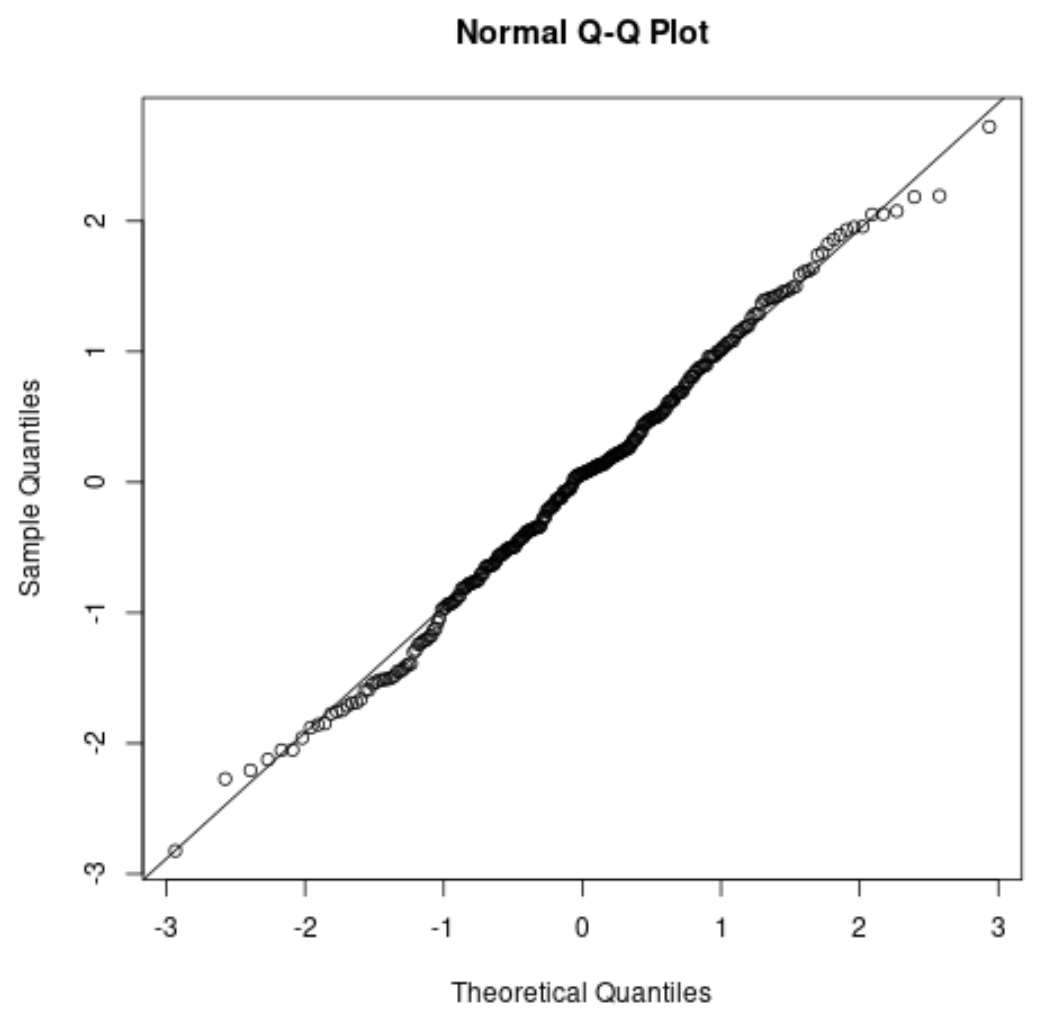
Связанный: Как использовать графики QQ для проверки нормальности

2. Проведите формальный статистический тест.

Вы также можете выполнить тест Шапиро-Уилка, чтобы проверить нормальность. Если значение p теста меньше 0,05, это говорит о том, что данные не распределены нормально.

Однако имейте в виду, что при работе с очень большими выборками статистические тесты, такие как тест Шапиро-Уилка, почти всегда сообщают вам, что ваши данные ненормальны.

По этой причине зачастую лучше всего визуально проверять данные с помощью диаграмм, таких как гистограммы и графики QQ. Просто взглянув на графики, можно получить довольно хорошее представление о том, нормально ли распределяются данные или нет.

Что делать, если это предположение не соблюдается

В целом, ANOVA с повторными измерениями считается достаточно устойчивым к нарушениям предположения о нормальности, если размеры выборки достаточно велики.

Если предположение о нормальности серьезно нарушено, у вас есть два варианта:

1. Преобразуйте значения ответа ваших данных так, чтобы распределения распределялись более нормально.

2. Выполните эквивалентный непараметрический тест, такой как тест Фридмана , который не требует предположения о нормальности.

Предположение 3: Сферичность

ANOVA с повторными измерениями предполагает сферичность – то есть дисперсии различий между всеми комбинациями связанных групп должны быть равны.

Если это предположение не выполняется, коэффициент F становится завышенным, а результаты повторных измерений ANOVA становятся ненадежными.

Как определить, выполняется ли это предположение

Чтобы проверить, выполняется ли это предположение, мы можем провести тест сферичности Мокли.

В этом тесте используются следующие нулевая и альтернативная гипотезы:

• H ₀ : Дисперсии разностей равны.
• H _A : Дисперсии разностей не равны.

Если значение p теста ниже определенного уровня значимости (например, α = 0,05), то мы отвергаем нулевую гипотезу и заключаем, что дисперсии различий не равны.

В противном случае, если значение p не меньше определенного уровня значимости (например, α = 0,05), мы не сможем отвергнуть нулевую гипотезу и сделать вывод, что предположение о сферичности выполнено.

В зависимости от статистического программного обеспечения, которое вы используете, результаты этого теста будут выглядеть следующим образом:

Поскольку значение p не меньше 0,05, мы не сможем отвергнуть нулевую гипотезу и сделать вывод, что предположение о сферичности выполняется в этом конкретном примере.

Что делать, если это предположение не соблюдается

Если мы отвергаем нулевую гипотезу теста сферичности Мокли, мы обычно применяем поправку к степеням свободы, используемым для расчета значения F в таблице ANOVA с повторными измерениями.

Мы можем применить три исправления:

• Хюинь-Фельдт (наименее консервативный)
• Серр-Гейссер
• Нижний предел (самый консервативный)

Каждая из этих поправок имеет тенденцию увеличивать значения p в выходной таблице ANOVA с повторными измерениями, чтобы учесть тот факт, что предположение о сферичности нарушается.

Затем мы можем использовать эти значения p, чтобы определить, следует ли нам отвергнуть нулевую гипотезу ANOVA с повторными измерениями.

Дополнительные ресурсы

В следующих руководствах представлена дополнительная информация о дисперсионном анализе с повторными измерениями:

Введение в повторяющиеся измерения ANOVA
Калькулятор повторяющихся измерений ANOVA
Как сообщить о результатах повторных измерений ANOVA
Однофакторный дисперсионный анализ и дисперсионный анализ с повторными измерениями: разница