Три гипотезы, сформулированные в парном t-тесте

T-критерий парных выборок используется для сравнения средних значений двух выборок, когда каждое наблюдение в одной выборке может быть связано с наблюдением в другой выборке.

Этот тип теста делает следующие предположения относительно данных:

1. Независимость: каждое наблюдение должно быть независимым от любого другого наблюдения.

2. Нормальность: различия между парами должны быть примерно нормально распределены.

3. Никаких резких выбросов: в различиях не должно быть никаких резких выбросов.

Если одно или несколько из этих допущений не выполняются, результаты t-критерия парных выборок могут быть ненадежными или вводящими в заблуждение.

В этом руководстве мы даем объяснение каждому предположению, как определить, выполняется ли предположение и что делать, если оно нарушается.

Гипотеза 1: Независимость

T-критерий парных выборок предполагает, что каждое наблюдение независимо от всех других наблюдений.

Как проверить эту гипотезу

Самый простой способ проверить это предположение — убедиться, что каждое наблюдение было собрано с использованием метода случайной выборки .

Если использовался метод случайной выборки (например, простая случайная выборка), то можно предположить, что каждое наблюдение независимо от всех других наблюдений.

Что делать, если это предположение не соблюдается

Если это предположение не выполняется, результаты t-критерия парных выборок полностью недействительны.

В этом сценарии лучше всего собирать новые наблюдения, используя метод случайной выборки, чтобы гарантировать независимость каждого наблюдения.

Гипотеза 2: нормальность

T-критерий для парных выборок предполагает, что различия между парами должны быть примерно нормально распределены.

Это важнейшее предположение, поскольку, если различия между парами не распределены нормально, недопустимо использовать значение p теста для выводов.

Как проверить эту гипотезу

Самый простой способ проверить эту гипотезу — просто создать гистограмму парных разностей и визуально проверить, имеет ли гистограмма колоколообразную форму.

Например, если гистограмма выглядит так, мы бы сказали, что предположение о нормальности выполнено:

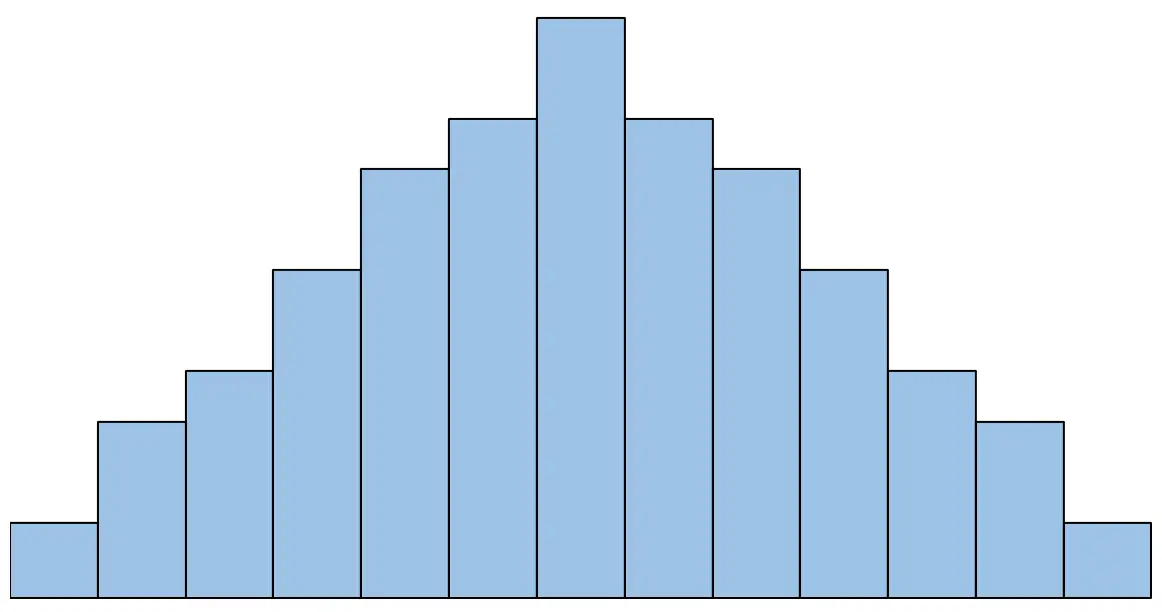
Однако, если гистограмма выглядит так, мы бы сказали, что предположение о нормальности не выполняется:

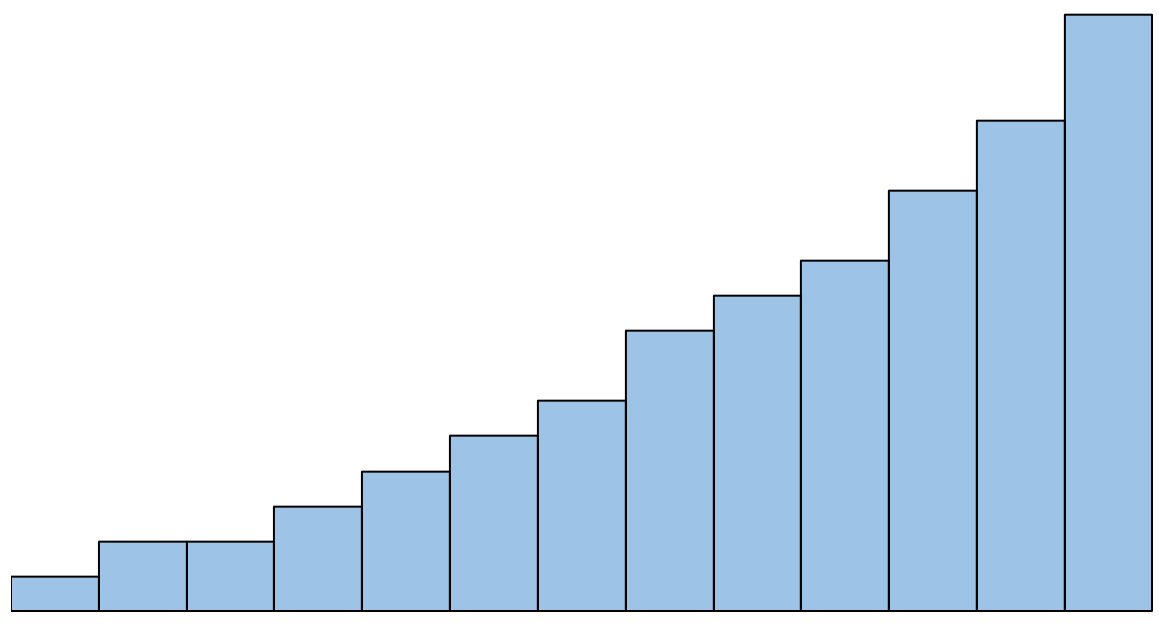
Что делать, если это предположение не соблюдается

Если это предположение нарушается, мы можем выполнить знаково-ранговый критерий Уилкоксона , который считается непараметрическим эквивалентом t-критерия для парных выборок и не предполагает, что парные различия имеют нормальное распределение.

Гипотеза 3: отсутствие экстремальных выбросов

T-критерий для парных выборок предполагает, что в данных нет экстремальных выбросов.

Как проверить эту гипотезу

Самый простой способ проверить эту гипотезу — создать коробчатую диаграмму парных различий и визуально проверить, есть ли какие-либо выбросы.

Например, предположим, что ящичковая диаграмма парных разностей выглядит следующим образом:

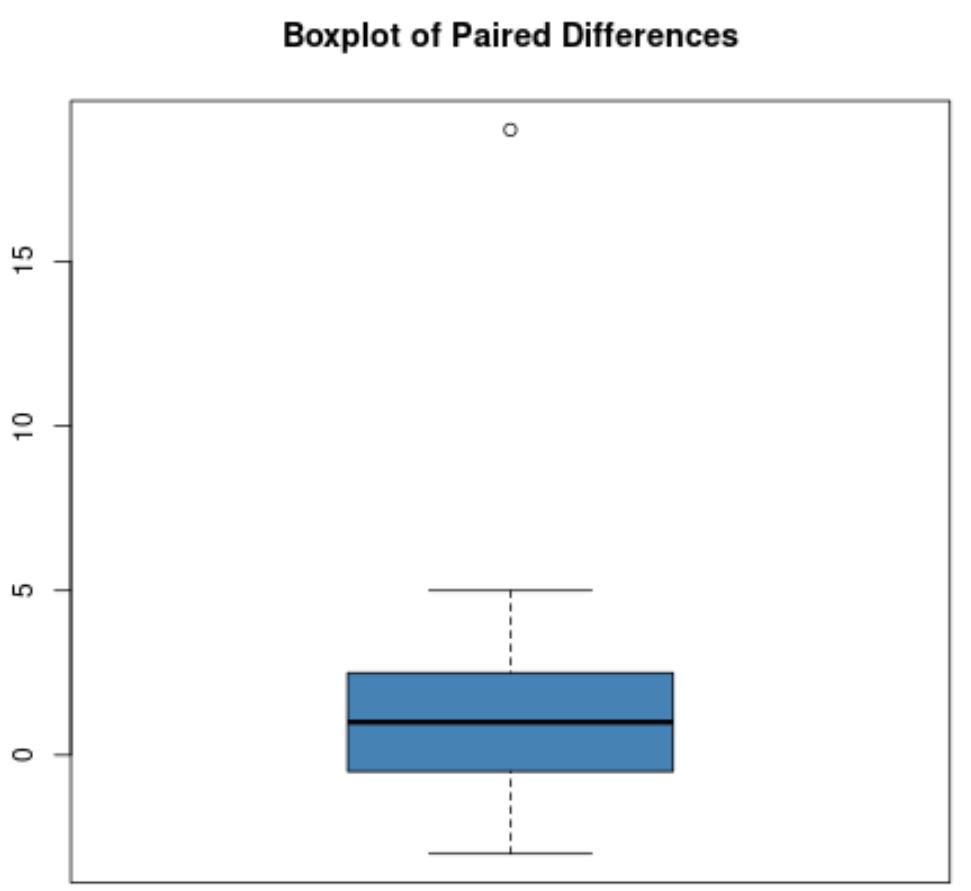
Большинство парных различий близки к нулю, но есть одно парное различие, равное примерно 19, что явно является выбросом.

Примечание . На ящичковой диаграмме обычно используется кружок, обозначающий выброс.

Однако предположим, что коробчатая диаграмма парных разностей выглядит следующим образом:

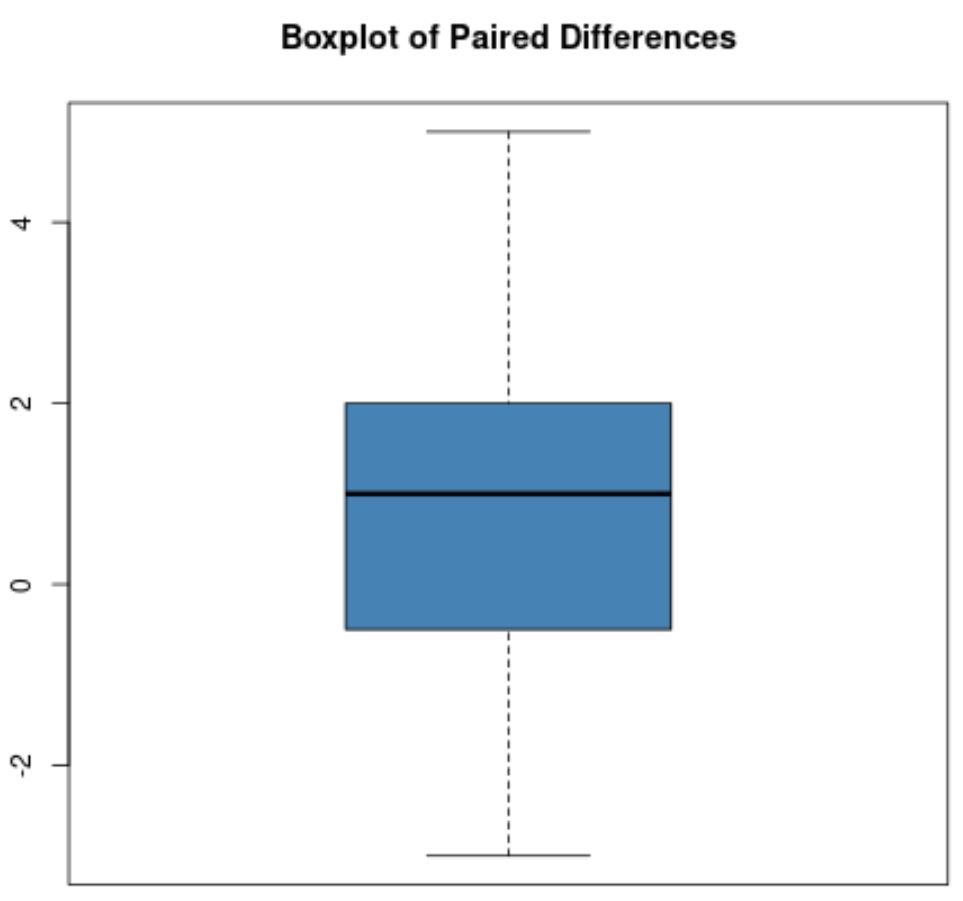
На этой диаграмме нет явных выбросов, поэтому мы будем предполагать, что в данных нет экстремальных выбросов.

Что делать, если это предположение не соблюдается

Если это предположение нарушается, выбросы могут аномально повлиять на результаты t-критерия парных выборок.

В этом сценарии вы можете удалить выброс, если считаете, что он представляет собой ошибочную точку данных или является результатом ошибки ввода данных.

Альтернативно, вы можете сохранить выброс и просто отметить его при сообщении о результатах t-теста для парных выборок.

Дополнительные ресурсы

В следующих руководствах объясняются предположения, сделанные в других статистических тестах:

Четыре гипотезы, сформулированные в t-тесте
Четыре гипотезы теста хи-квадрат
Четыре гипотезы параметрических тестов