Критическое значение

К бенджамин андерсон 3 августа, 2023 Статистика 0 комментариев

В этой статье объясняется, что такое критическая ценность в статистике и как ее следует интерпретировать при проверке гипотез. Кроме того, вы сможете увидеть, как рассчитывается критическое значение, а также несколько конкретных примеров.

Что такое критическая ценность?

Критическое значение — это точка распределения тестовой статистики, которая отделяет область отклонения нулевой гипотезы от области ее принятия. Другими словами, критическое значение — это значение распределения статистического теста, которое отмечает границу области отклонения (или критической области).

Обычно критическое значение обозначается символом Z _α/2 , поскольку наиболее распространенным эталонным распределением обычно является стандартное нормальное распределение .

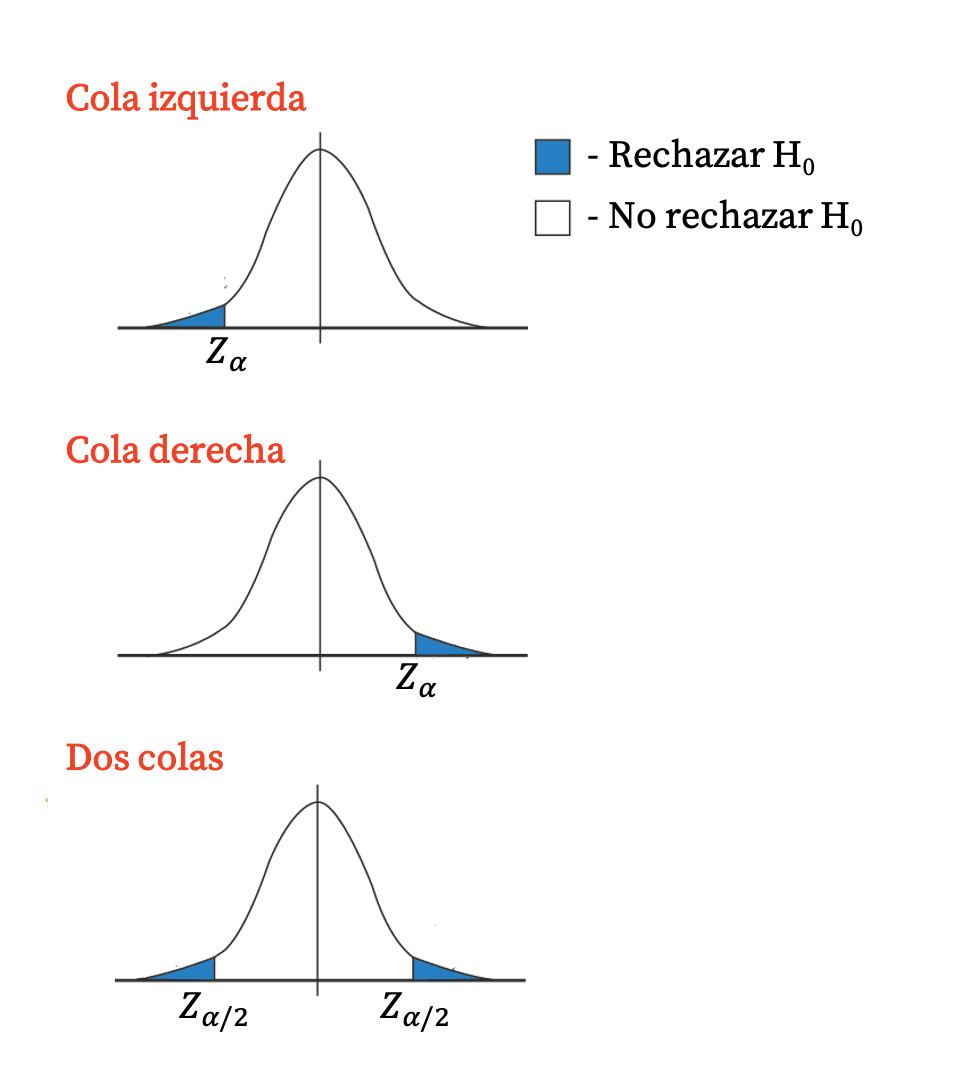
В общем, односторонние тесты имеют решающее значение, поскольку область отбраковки представляет собой единственный хвост распределения. С другой стороны, двусторонние тесты имеют два критических значения, поскольку область отклонения соответствует обоим хвостам распределения.

В доверительных интервалах критическими значениями являются точки эталонного распределения, обозначающие пределы доверительного интервала.

Как рассчитать критическое значение

Затем мы увидим, как рассчитываются наиболее распространенные критические значения. Критическое значение Z и критическое значение t рассчитываются для доверительного интервала среднего значения, с той лишь разницей, что критическое значение Z рассчитывается, когда известно стандартное отклонение генеральной совокупности, и вместо этого используется критическое значение t. когда известны данные только по одному образцу.

Критическое значение Z

Критическое значение Z используется для определения границ доверительного интервала среднего значения. Точнее, он используется только в том случае, если вы знаете стандартное отклонение генеральной совокупности.

Для расчета критического значения Z необходимо найти значение, соответствующее вероятности половины уровня значимости, в стандартной таблице нормального распределения .

Например, если мы хотим определить доверительный интервал для среднего значения с уровнем достоверности 95%, это означает, что уровень значимости равен 5%. Поэтому необходимо посмотреть в таблице стандартного нормального распределения, какое значение соответствует вероятности 2,5%, так как доверительный интервал для среднего двусторонний.

$1-\alpha=0,95 \ \color{orange}\bm{\longrightarrow}\color{black} \ \alpha=0,05 \ \color{orange}\bm{\longrightarrow}\color{black}\ \alpha/2=0,025$

$\begin{array}{c}Z_{\alpha/2}= \ \color{orange}\bm{?}\\[4ex]Z_{0,025}=1,96\end{array}$

Ниже вы можете увидеть таблицу с наиболее часто используемыми критическими значениями Z:

Уровень уверенности (1-α)	Уровень значимости (α)	Критическое значение (Z _α/2 )
0,80	0,20	1282
0,85	0,15	1440
0,90	0,10	1645
0,95	0,05	1960 год
0,99	0,01	2576
0,995	0,005	2807
0,999	0,001	3,291

Критическое значение t

Критическое значение t используется для определения границ доверительного интервала для среднего значения, когда стандартное отклонение генеральной совокупности неизвестно.

Для расчета критического значения t в таблице распределения t Стьюдента необходимо найти значение, соответствующее вероятности половины уровня значимости, принимая во внимание, что степени свободы распределения t Стьюдента имеют единицу. чем размер выборки.

Например, если мы хотим найти доверительный интервал с уровнем достоверности 95% и размером выборки 8, нам нужно получить доступ к таблице распределения Стьюдента и посмотреть, какое значение соответствует t _0,025|7 .

$1-\alpha=0,95 \ \color{orange}\bm{\longrightarrow}\color{black} \ \alpha=0,05 \ \color{orange}\bm{\longrightarrow}\color{black}\ \alpha/2=0,025$

$\begin{array}{c}t_{\alpha/2| n-1}= \ \color{orange}\bm{?}\\[4ex]t_{0,025| 7}=2,365\end{array}$

➤ См.: Как рассчитать доверительный интервал среднего значения.

Критическая ценность в проверке гипотез

Критическое значение также можно использовать при проверке гипотез, чтобы отвергнуть нулевую гипотезу (и принять альтернативную гипотезу) или отвергнуть альтернативную гипотезу (и принять нулевую гипотезу).

Если значение распределения тестовой статистики, соответствующее значению p, лежит в пределах интервала, отмеченного критическими значениями, нулевая гипотеза не отклоняется (альтернативная гипотеза отклоняется).
Если значение распределения тестовой статистики, соответствующее значению p, находится за пределами интервала, отмеченного критическими значениями, нулевая гипотеза отклоняется (принимается альтернативная гипотеза).

Об авторе

бенджамин андерсон

Здравствуйте, я Бенджамин, профессор статистики на пенсии, ставший преданным преподавателем Statorials. Имея обширный опыт и знания в области статистики, я хочу поделиться своими знаниями, чтобы расширить возможности студентов с помощью Statorials. Узнать больше