Выборочное распределение среднего значения

К бенджамин андерсон 3 августа, 2023 Статистика 0 комментариев

В этой статье объясняется, что такое выборочное распределение среднего значения в статистике. Вы также найдете формулу распределения выборки среднего значения и пошаговое решение упражнения.

Каково выборочное распределение среднего значения?

Выборочное распределение среднего (или выборочное распределение средних ) — это распределение, которое получается в результате расчета выборочного среднего для каждой возможной выборки из совокупности. То есть набор выборочных средних из всех возможных выборок генеральной совокупности образует выборочное распределение среднего.

Другими словами, если мы изучаем все выборки, которые можно взять из совокупности, и вычисляем среднее значение каждой из выборок, набор рассчитанных значений образует выборочное распределение выборочного среднего.

В статистике выборочное распределение среднего значения используется для расчета вероятности приближения к значению среднего значения генеральной совокупности при анализе одной выборки.

Формула выборочного распределения среднего значения

Учитывая популяцию, которая следует нормальному распределению вероятностей со средним значением

$\mu$

и стандартное отклонение

$\sigma$

и образцы размеров извлекаются

$n$

, выборочное распределение среднего значения также будет определяться нормальным распределением, имеющим следующие характеристики:

$\begin{array}{c}\mu_{\overline{x}}=\mu \qquad \sigma_{\overline{x}}=\cfrac{\sigma}{\sqrt{n}}\\[4ex]\displaystyle N_{\overline{x}}\left(\mu, \frac{\sigma}{\sqrt{n}}\right) \end{array}$

Золото

$\mu_{\overline{x}}$

является средним значением выборочного распределения среднего и

$\sigma_{\overline{x}}$

это его стандартное отклонение. Более того,

$\cfrac{\sigma}{\sqrt{n}}$

— стандартная ошибка выборочного распределения.

Примечание. Если генеральная совокупность не подчиняется нормальному распределению, но размер выборки велик (n>30), выборочное распределение среднего значения также можно аппроксимировать к предыдущему нормальному распределению с помощью центральной предельной теоремы.

Следовательно, поскольку выборочное распределение среднего значения соответствует нормальному распределению, формула для расчета любой вероятности, связанной с выборочным средним, выглядит следующим образом:

$Z=\cfrac{\overline{x}-\mu}{\displaystyle\frac{\sigma}{\sqrt{n}}}$

Золото:

$\overline{x}$

это образец означает.
$\mu$

Это средний показатель по численности населения.
$s$

— стандартное отклонение генеральной совокупности.
$n$

это размер выборки.
$Z$

— переменная, определяемая стандартным нормальным распределением N(0,1).

Реальный пример выборочного распределения среднего значения

Увидев определение выборочного распределения среднего значения и связанные с ним формулы, давайте решим пример, чтобы лучше понять эту концепцию.

Вес студентов университетов подчиняется нормальному распределению со средним значением 68 кг и стандартным отклонением 9 кг. Определенный:
1. Какова вероятность того, что средний вес случайной выборки из 25 студентов будет меньше 66 кг?
2. Если взять 300 проб по 25 учащихся в каждой, сколько средних значений выборки будет иметь значение менее 66 кг?

Прежде всего, мы должны рассчитать значение соответствующей статистики, для этого применим формулу, которую мы видели выше:

$\displaystyle Z=\frac{\overline{x}-\mu}{\displaystyle\frac{\sigma}{\sqrt{n}}}=\frac{66-68}{\displaystyle\frac{9}{\sqrt{25}}}=-1,11$

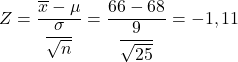
Таким образом, искомая вероятность соответствует значению Z=-1,11 левого хвоста стандартного нормального распределения, которое можно легко получить из таблицы вероятностей Z. Поэтому мы используем таблицу Z, чтобы определить вероятность того, что проблема задаст нам вопрос:

$P[\overline{x}\leq 66]=P[Z\leq -1,11] =0,1335$

➤ См.: Таблица Z.

Теперь, когда мы знаем вероятность того, что среднее значение случайной выборки будет меньше 66 кг, чтобы узнать среднее количество образцов меньше 66 кг, взяв 300 равных образцов, нам нужно умножить рассчитанную вероятность на общее количество взятых образцов:

$0,1335\cdot 300 =40,05 \approx 40$

Таким образом, примерно 40 извлеченных проб будут иметь средний вес менее 66 кг.

Об авторе

бенджамин андерсон

Здравствуйте, я Бенджамин, профессор статистики на пенсии, ставший преданным преподавателем Statorials. Имея обширный опыт и знания в области статистики, я хочу поделиться своими знаниями, чтобы расширить возможности студентов с помощью Statorials. Узнать больше

Каково выборочное распределение среднего значения?

Формула выборочного распределения среднего значения

Реальный пример выборочного распределения среднего значения

Об авторе

бенджамин андерсон

Добавить комментарий