Выборочное распределение разницы в пропорциях
В этой статье объясняется, в чем разница в распределении пропорциональной выборки и для чего она используется в статистике. Также представлены разница в формуле распределения выборки по пропорциям и пошаговое решение упражнения.
Каково выборочное распределение разницы в пропорциях?
Разница в распределении выборки по пропорциям — это распределение, которое получается в результате расчета различий между долями выборки всех возможных выборок из двух разных совокупностей.
То есть процесс получения выборочного распределения разницы в пропорциях заключается, во-первых, в извлечении всех возможных выборок из двух разных популяций, во-вторых, в определении доли каждой извлеченной выборки и, наконец, в определении разницы между всеми пропорции разницы пропорций. две популяции. Так что совокупность результатов, полученных после выполнения этих операций, образует выборочное распределение разницы пропорций.

В статистике разница в выборочном распределении пропорций используется для расчета вероятности того, что разница между долями выборки двух случайно выбранных выборок близка к разнице долей генеральной совокупности.
Формула выборочного распределения разности пропорций
Выборки, отобранные по разнице в пропорциях выборочного распределения, определяются биномиальными распределениями , поскольку для практических целей пропорция представляет собой отношение успешных случаев к общему числу наблюдений.
Тем не менее, благодаря центральной предельной теореме, биномиальные распределения можно аппроксимировать к нормальным распределениям вероятностей . Следовательно, выборочное распределение разницы в пропорциях можно приблизить к нормальному распределению со следующими характеристиками:
![Rendered by QuickLaTeX.com \begin{array}{c}\displaystyle\mu_{\widehat{p_1}-\widehat{p_2}}=p_1-p_2 \qquad \sigma_{\widehat{p_1}-\widehat{p_2}}=\sqrt{\frac{p_1q_1}{n_1}+\frac{p_2q_2}{n_2}}\\[6ex]\displaystyle N_{p}\left(p_1-p_2, \sqrt{\frac{p_1q_1}{n_1}+\frac{p_2q_2}{n_2}}\right) \end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-a1ce359b5dd6d80f8d27b0b9a1034bed_l3.png)
Примечание. Выборочное распределение разницы в пропорциях можно приблизить к нормальному распределению только в том случае, если
![]()
,
![]()
,
![]()
,
![]()
,
![]()
И
![]()
.
Следовательно, поскольку выборочное распределение разницы долей можно приблизить к нормальному распределению, то формула расчета статистики выборочного распределения разницы долей имеет следующий вид:

Золото:
-

– это выборочная доля i.
-

это доля населения i.
-

— вероятность отказа популяции i,

.
-

размер выборки i.
-

— переменная, определяемая стандартным нормальным распределением N(0,1).
Эта формула аналогична формуле проверки гипотезы для разницы в пропорциях.
Конкретный пример выборочного распределения разницы долей
Увидев определение разницы в пропорциях выборочного распределения и какова его формула, вы можете шаг за шагом увидеть ниже решенный пример, чтобы завершить понимание концепции.
- Вы хотите проанализировать точность двух производственных предприятий: один завод производит так, что только 5% выпускаемых деталей имеют дефекты, а на другом заводе процент бракованных деталей составляет 8%. Если мы возьмем образец из 200 деталей с первого завода и еще один образец из 280 деталей со второго завода, какова вероятность того, что процент брака на первом заводе больше, чем процент брака на втором заводе? производство?
Чтобы закончить знание всех данных задачи, сначала посчитаем долю хорошо продуцируемых частей каждого растения:
![Rendered by QuickLaTeX.com \begin{array}{c}q_1=1-p_1=1-0,05=0,95\\[2ex]q_2=1-p_2=1-0,08=0,92\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-7c02732cc5fb319bfa5bf7b8ed8d03db_l3.png)
Если уровень брака на первом заводе был больше, чем уровень брака на втором заводе, это означает, что следующее уравнение будет верным:
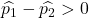
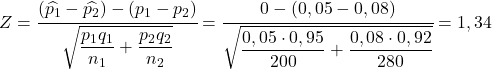
Таким образом, вероятность того, что уровень дефектов первой фабрики превышает уровень дефектов второй фабрики, эквивалентна вероятности того, что переменная Z больше 1,34:
![P[(\widehat{p_1}-\widehat{p_2})>0]=P[Z>1,34]» title=»Rendered by QuickLaTeX.com» height=»19″ width=»242″ style=»vertical-align: -5px;»></p>
</p>
<p> Наконец, нам просто нужно поискать соответствующую вероятность в <a href=](https://statorials.org/wp-content/ql-cache/quicklatex.com-41dd897cdff473ff488cde0e3cc140b0_l3.png) таблице нормального распределения и мы уже решим задачу:
таблице нормального распределения и мы уже решим задачу:
![P[(\widehat{p_1}-\widehat{p_2})>0]=P[Z>1,34]=0,0901″ title=»Rendered by QuickLaTeX.com» height=»19″ width=»319″ style=»vertical-align: -5px;»></p>
</p>
<p> Короче говоря, вероятность того, что доля дефектов на первом заводе больше, чем доля дефектов на втором заводе, составляет 9,01%. </p>
<div style=](https://statorials.org/wp-content/ql-cache/quicklatex.com-8d6e503a2089d30be8fd68bbc722bb44_l3.png)