Качество посадки
В этой статье объясняется, что такое степень соответствия в статистике. Кроме того, здесь показано, как измерить степень соответствия регрессионной модели, и, кроме того, вы сможете увидеть решенное упражнение на степень соответствия.
Что такое доброта соответствия?
В статистике степень соответствия — это то, насколько хорошо регрессионная модель соответствует выборке данных. Другими словами, степень соответствия регрессионной модели относится к уровню связи между набором наблюдений и значениями, полученными с помощью регрессии.
Следовательно, чем лучше подходит регрессионная модель, тем лучше она объясняет изучаемые данные. Таким образом, мы хотим, чтобы чем лучше статистическая модель соответствовала, тем лучше.
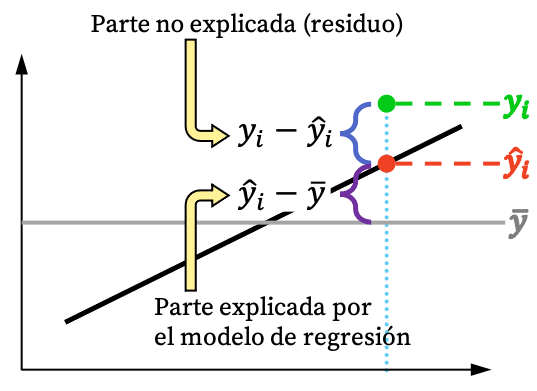
Как вы можете видеть на изображении выше, ценность наблюдения обычно не может быть полностью объяснена с помощью регрессионной модели. Но логически, чем больше регрессионная модель может объяснить из набора данных, тем лучше она подойдет. Короче говоря, нас интересует максимально точная регрессионная модель.
Степень соответствия регрессионной модели
Чтобы определить степень соответствия регрессионной модели, обычно используют коэффициент детерминации , который представляет собой статистический коэффициент, указывающий процент, объясняемый регрессионной моделью. Таким образом, чем выше коэффициент детерминации модели, тем лучше модель будет адаптирована к выборке данных.
![]()
Однако следует отметить, что чем больше переменных имеет регрессионная модель, тем выше будет ее коэффициент детерминации. По этой причине скорректированный коэффициент детерминации также часто используется для измерения степени соответствия модели. Скорректированный коэффициент детерминации представляет собой вариацию предыдущего коэффициента, который указывает процент, объясненный регрессионной моделью, с наложением штрафов за каждую объясняющую переменную, включенную в модель.
![]()
Поэтому предпочтительнее использовать скорректированный коэффициент детерминации для сравнения двух моделей с рядом различных переменных, поскольку он учитывает количество переменных, включенных в модель.
Наконец, следует отметить, что критерий Хи-квадрат также можно использовать для измерения степени соответствия регрессионной модели, хотя обычно используются значения двух предыдущих коэффициентов.
Конкретный пример хорошего соответствия
Наконец, мы увидим решающее упражнение по качеству корректировки, чтобы завершить усвоение этой статистической концепции.
- С одним и тем же рядом данных выполняются две разные модели линейной регрессии, результаты которых вы можете увидеть в следующей таблице. Какую модель лучше всего использовать?
| Регрессионная модель 1 | Регрессионная модель 2 | |
|---|---|---|
| Коэффициент детерминации | 57% | 64% |
| Скорректированный коэффициент детерминации | 49% | 43% |
| Количество объясняющих переменных | 3 | 7 |
В этом случае мы предполагаем, что обе модели удовлетворяют предыдущим предположениям моделей линейной регрессии, и, следовательно, нам нужно только проанализировать степень соответствия моделей.
Регрессионная модель 2 имеет более высокий коэффициент детерминации, чем регрессионная модель 1, поэтому она априори кажется лучшей регрессионной моделью, поскольку она способна лучше объяснить выборку данных.
Однако модель регрессии 2 имеет 7 независимых переменных в модели, а модель регрессии 1 — только 3. Таким образом, модель 2 будет намного сложнее и ее труднее интерпретировать, чем первую модель.
Кроме того, если мы посмотрим на скорректированный коэффициент детерминации, который учитывает количество переменных в модели, регрессионная модель 1 имеет более высокий скорректированный коэффициент детерминации, чем регрессионная модель 2.
В заключение, хотя лучше использовать регрессионную модель 1, поскольку ее скорректированный коэффициент детерминации выше, чем у регрессионной модели 2. Регрессионная модель 2 имеет более высокий нескорректированный коэффициент детерминации, это потому, что они включили в регрессию гораздо больше переменных. Модель 1. Модель, которая увеличивает значение указанного коэффициента, но усложняет интерпретацию модели и, конечно же, ухудшает прогноз нового значения.
Для сравнения моделей с разным количеством переменных лучше всего использовать скорректированный коэффициент детерминации, поскольку он накладывает штрафы за каждую добавленную в модель переменную. Как вы видели в этом примере, согласно нескорректированному коэффициенту детерминации, регрессионная модель 2 лучше, однако с помощью скорректированного коэффициента детерминации мы можем знать, что регрессионная модель 1 на самом деле лучше.