Как проверить нормальность в python (4 метода)
Многие статистические тесты предполагают , что наборы данных распределены нормально.
Есть четыре распространенных способа проверить эту гипотезу в Python:
1. (Визуальный метод) Создайте гистограмму.
- Если гистограмма имеет приблизительно форму «колокола», то предполагается, что данные распределены нормально.
2. (Визуальный метод) Создайте график QQ.
- Если точки на графике лежат примерно вдоль прямой диагональной линии, то предполагается, что данные распределены нормально.
3. (Формальный статистический тест) Выполните тест Шапиро-Уилка.
- Если значение p теста больше α = 0,05, то предполагается, что данные распределены нормально.
4. (Формальный статистический тест) Выполните тест Колмогорова-Смирнова.
- Если значение p теста больше α = 0,05, то предполагается, что данные распределены нормально.
Следующие примеры показывают, как использовать каждый из этих методов на практике.
Метод 1: создайте гистограмму
Следующий код показывает, как создать гистограмму для набора данных, который соответствует логарифмически нормальному распределению :
import math
import numpy as np
from scipy. stats import lognorm
import matplotlib. pyplot as plt
#make this example reproducible
n.p. random . seeds (1)
#generate dataset that contains 1000 log-normal distributed values
lognorm_dataset = lognorm. rvs (s=.5, scale= math.exp (1), size=1000)
#create histogram to visualize values in dataset
plt. hist (lognorm_dataset, edgecolor=' black ', bins=20)
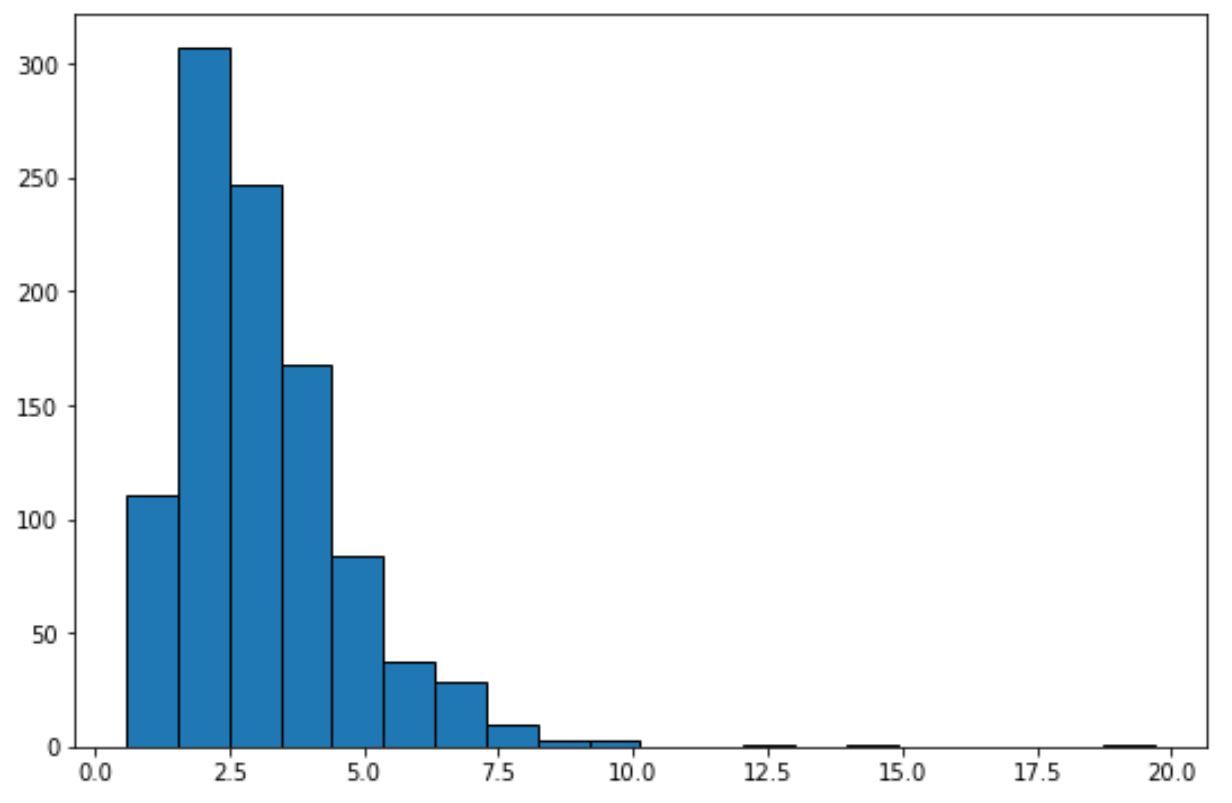
Просто взглянув на эту гистограмму, мы можем сказать, что набор данных не имеет «колоколообразной формы» и не имеет нормального распределения.
Метод 2: Создайте график QQ
Следующий код показывает, как создать график QQ для набора данных, который соответствует логарифмически нормальному распределению:
import math
import numpy as np
from scipy. stats import lognorm
import statsmodels. api as sm
import matplotlib. pyplot as plt
#make this example reproducible
n.p. random . seeds (1)
#generate dataset that contains 1000 log-normal distributed values
lognorm_dataset = lognorm. rvs (s=.5, scale= math.exp (1), size=1000)
#create QQ plot with 45-degree line added to plot
fig = sm. qqplot (lognorm_dataset, line=' 45 ')
plt. show ()
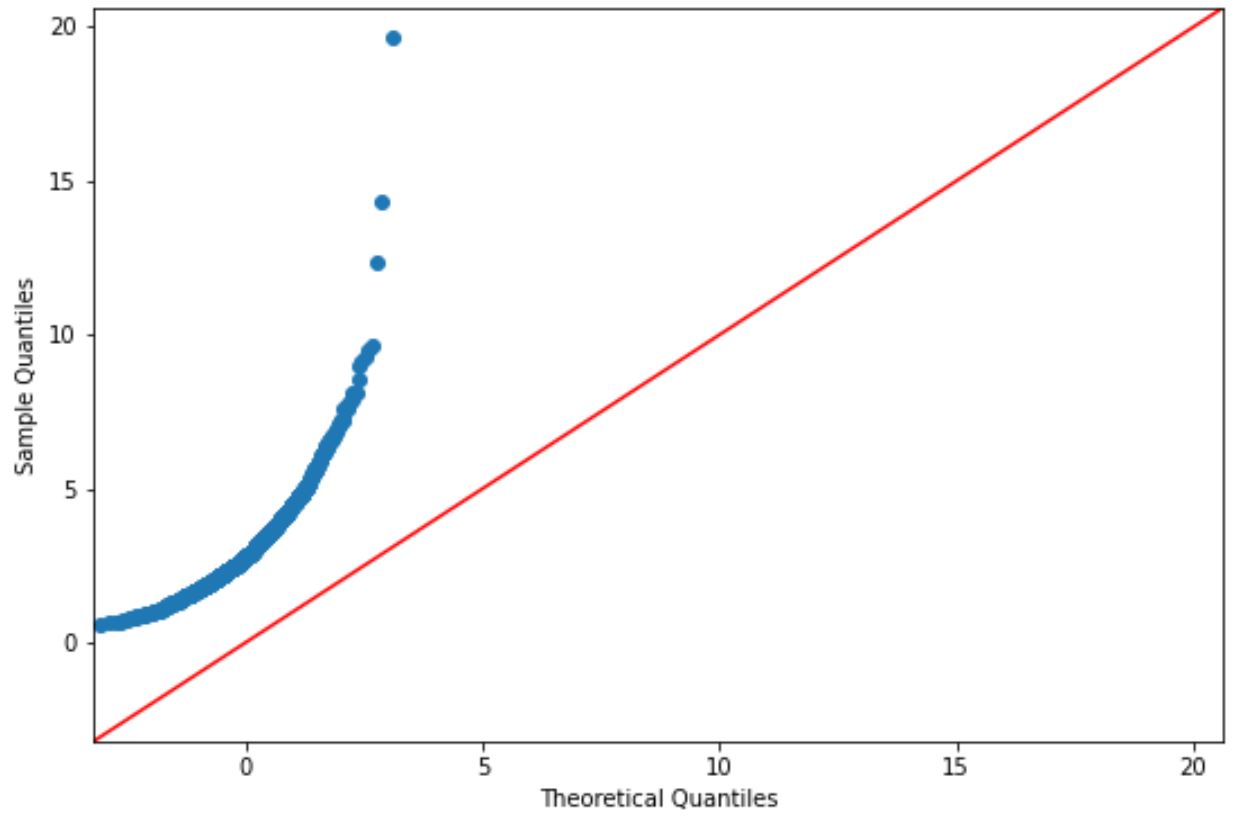
Если точки графика лежат примерно вдоль прямой диагональной линии, мы обычно предполагаем, что набор данных нормально распределен.
Однако точки на этом графике явно не соответствуют красной линии, поэтому мы не можем считать, что этот набор данных нормально распределен.
Это должно иметь смысл, учитывая, что мы сгенерировали данные, используя функцию логнормального распределения.
Метод 3. Проведите тест Шапиро-Уилка.
Следующий код показывает, как выполнить анализ Шапиро-Уилка для набора данных, который соответствует логарифмически нормальному распределению:
import math
import numpy as np
from scipy.stats import shapiro
from scipy. stats import lognorm
#make this example reproducible
n.p. random . seeds (1)
#generate dataset that contains 1000 log-normal distributed values
lognorm_dataset = lognorm. rvs (s=.5, scale= math.exp (1), size=1000)
#perform Shapiro-Wilk test for normality
shapiro(lognorm_dataset)
ShapiroResult(statistic=0.8573324680328369, pvalue=3.880663073872444e-29)
Из результата мы видим, что статистика теста равна 0,857 , а соответствующее значение p составляет 3,88e-29 (чрезвычайно близко к нулю).
Поскольку значение p меньше 0,05, мы отвергаем нулевую гипотезу теста Шапиро-Уилка.
Это означает, что у нас есть достаточно доказательств, чтобы сказать, что выборочные данные не имеют нормального распределения.
Метод 4: выполнить тест Колмогорова-Смирнова.
Следующий код показывает, как выполнить тест Колмогорова-Смирнова для набора данных, который соответствует логнормальному распределению:
import math
import numpy as np
from scipy.stats import kstest
from scipy. stats import lognorm
#make this example reproducible
n.p. random . seeds (1)
#generate dataset that contains 1000 log-normal distributed values
lognorm_dataset = lognorm. rvs (s=.5, scale= math.exp (1), size=1000)
#perform Kolmogorov-Smirnov test for normality
kstest(lognorm_dataset, ' norm ')
KstestResult(statistic=0.84125708308077, pvalue=0.0)
Из результата мы видим, что статистика теста равна 0,841 , а соответствующее значение p равно 0,0 .
Поскольку значение p меньше 0,05, мы отвергаем нулевую гипотезу теста Колмогорова-Смирнова.
Это означает, что у нас есть достаточно доказательств, чтобы сказать, что выборочные данные не имеют нормального распределения.
Как обрабатывать нестандартные данные
Если данный набор данных не является нормально распределенным, мы часто можем выполнить одно из следующих преобразований, чтобы сделать его более нормально распределенным:
1. Преобразование журнала: преобразуйте значения x в log(x) .
2. Преобразование квадратного корня: преобразуйте значения x в √x .
3. Преобразование корня куба: преобразуйте значения x в x 1/3 .
Выполняя эти преобразования, набор данных обычно становится более нормально распределенным.
Прочтите это руководство , чтобы узнать, как выполнить эти преобразования в Python.