Как выполнить анализ главных компонентов в sas

Анализ главных компонентов (PCA) — это метод машинного обучения без учителя , целью которого является поиск основных компонентов — линейных комбинаций переменных-предсказателей — которые объясняют большую часть изменений в наборе данных.

Самый простой способ выполнить PCA в SAS — использовать оператор PROC PRINCOMP , который использует следующий базовый синтаксис:

 proc princomp data =my_data out =out_data outstat =stats;
    var var1 var2 var3;
run ;

Вот что делает каждая инструкция:

• data : имя набора данных, который будет использоваться для PCA.
• out : имя создаваемого набора данных, содержащего все исходные данные плюс оценки главных компонентов.
• outstat : указывает, что должен быть создан набор данных, содержащий средние значения, стандартные отклонения, коэффициенты корреляции, собственные значения и собственные векторы.
• var : переменные, которые будут использоваться для PCA из входного набора данных.

В следующем пошаговом примере показано, как на практике использовать оператор PROC PRINCOMP для выполнения анализа главных компонентов в SAS.

Шаг 1. Создайте набор данных

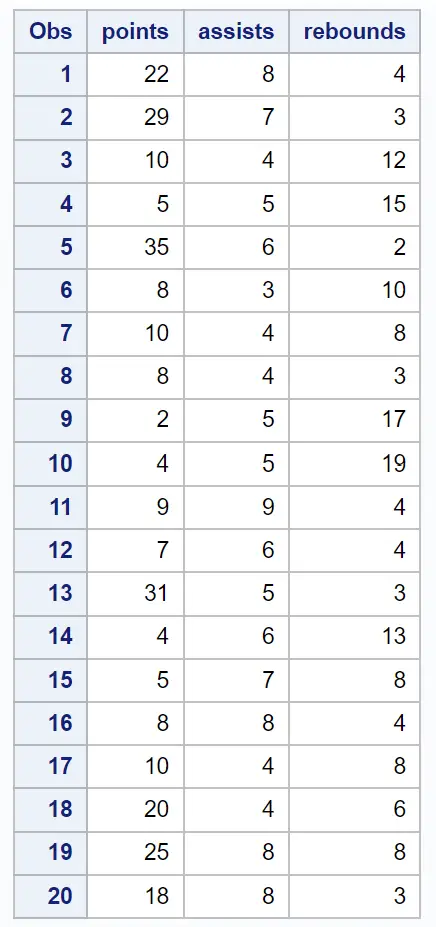
Предположим, у нас есть следующий набор данных, содержащий различную информацию о 20 баскетболистах:

 /*create dataset*/
data my_data;
    input points assists rebounds;
    datalines ;
22 8 4
29 7 3
10 4 12
5 5 15
35 6 2
8 3 10
10 4 8
8 4 3
2 5 17
4 5 19
9 9 4
7 6 4
31 5 3
4 6 13
5 7 8
8 8 4
10 4 8
20 4 6
25 8 8
18 8 3
;
run ;

/*view dataset*/
proc print data =my_data; 

Шаг 2. Выполните анализ главных компонентов

Мы можем использовать оператор PROC PRINCOMP для выполнения анализа главных компонентов с использованием переменных Points , Assets и Bounces набора данных:

 /*perform principal components analysis*/
proc princomp data =my_data out =out_data outstat =stats;
    var points assists rebounds;
run ;

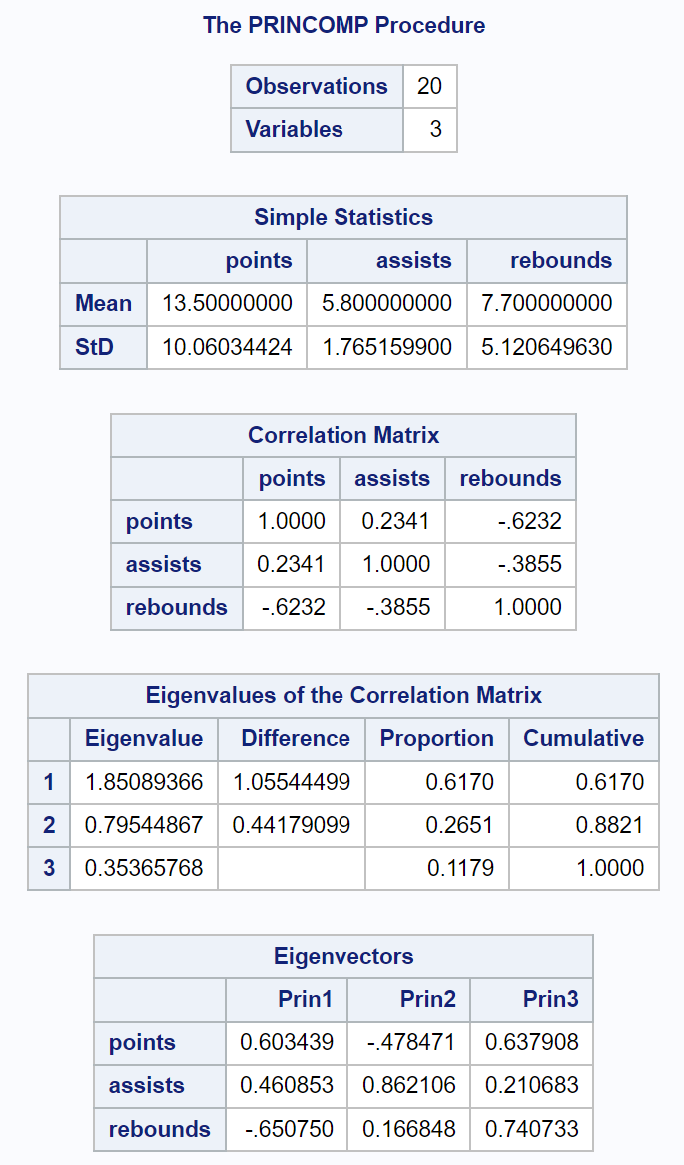
Первая часть вывода отображает различную описательную статистику, включая средние и стандартные отклонения каждой входной переменной, матрицу корреляции и значения собственных значений и собственных векторов:

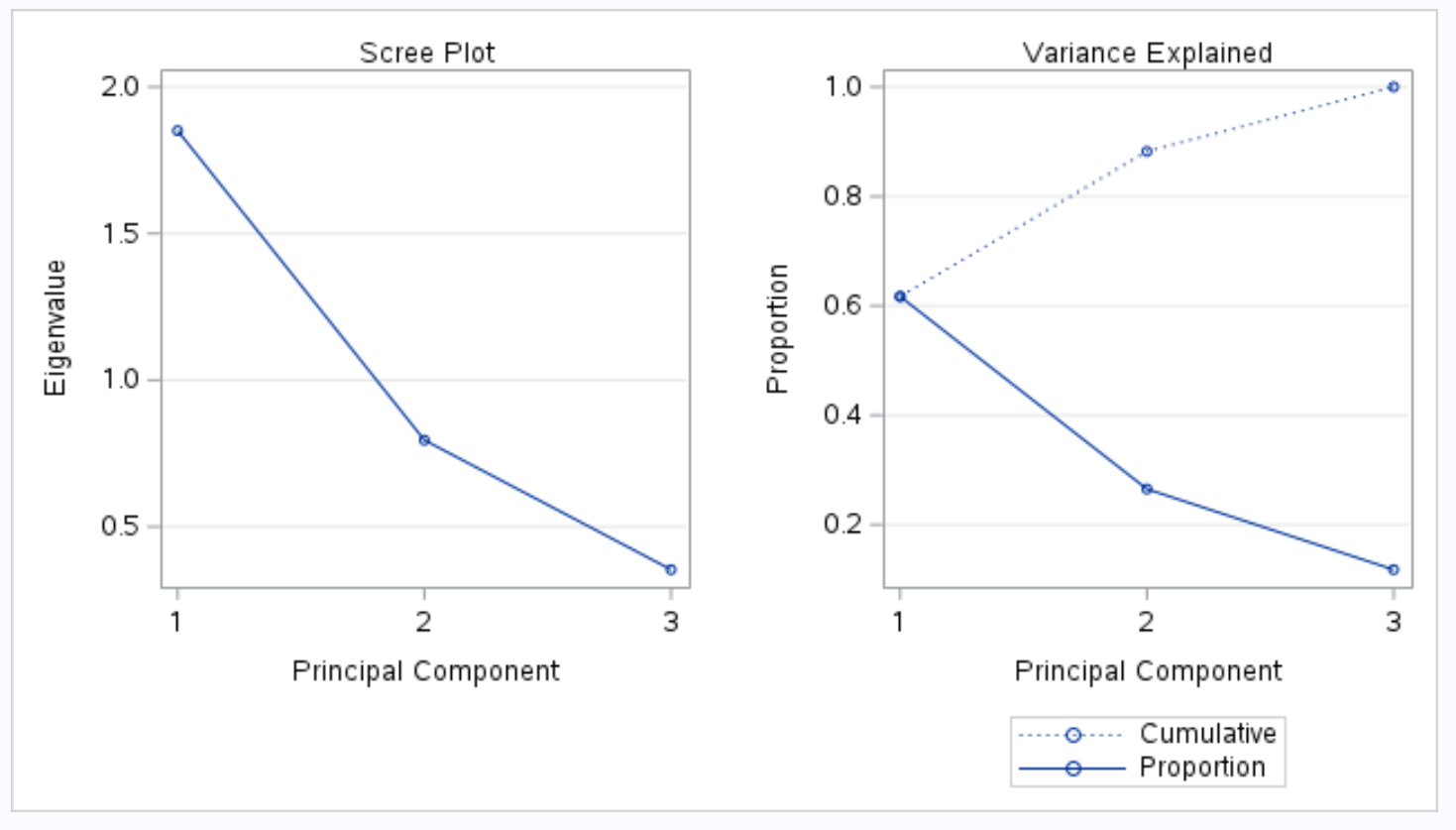
Следующая часть вывода отображает график осыпи и график объясненной дисперсии :

Когда мы выполняем PCA, мы часто хотим понять, какой процент от общего изменения набора данных можно объяснить каждым основным компонентом.

Полученная таблица под названием «Собственные значения корреляционной матрицы» позволяет нам увидеть, какой именно процент общей вариации объясняется каждым главным компонентом:

• Первый главный компонент объясняет 61,7% общей вариации в наборе данных.
• Второй главный компонент объясняет 26,51% общей вариации набора данных.
• Третий главный компонент объясняет 11,79% общей вариации в наборе данных.

Обратите внимание, что все проценты в сумме составляют 100%.

График под названием «Объяснение дисперсии» позволяет нам визуализировать эти значения.

По оси X отображается главный компонент, а по оси Y отображается процент общей дисперсии, объясняемой каждым отдельным основным компонентом.

Шаг 3. Создайте побочную диаграмму для визуализации результатов.

Чтобы визуализировать результаты PCA для данного набора данных, мы можем создать биплот , который представляет собой график, отображающий каждое наблюдение в наборе данных на плоскости, образованной первыми двумя главными компонентами.

Мы можем использовать следующий синтаксис в SAS для создания биграфика:

 /*create dataset with column called obs to represent row numbers of original data*/
data biplot_data;
   set out_data;
   obs=_n_;
run ;

/*create biplot using values from first two principal components*/
proc sgplot data =biplot_data;
    scatter x =Prin1 y =Prin2 / datalabel =obs;
run ; 

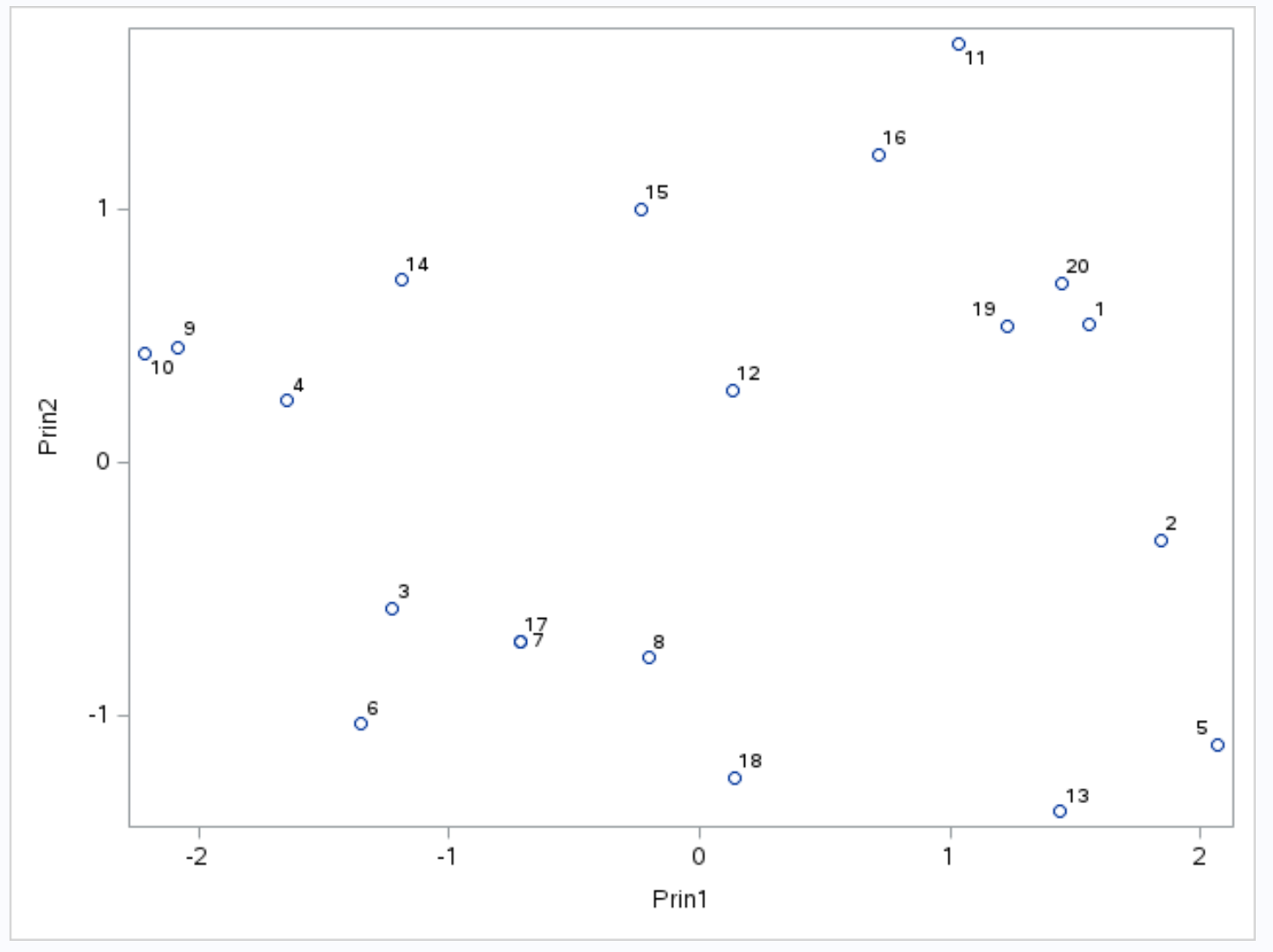
По оси X отображается первый главный компонент, по оси Y — второй главный компонент, а отдельные наблюдения из набора данных отображаются внутри графика в виде маленьких кружков.

Наблюдения, расположенные рядом на графике, имеют схожие значения для трех переменных: очков , передач и подборов .

Например, в крайнем левом углу графика мы видим, что наблюдения №9 и №10 очень близки друг к другу.

Если мы обратимся к исходному набору данных, мы увидим следующие значения для этих наблюдений:

• Наблюдение №9 : 2 очка, 5 передач, 17 подборов.
• Наблюдение №10 : 4 очка, 5 передач, 19 подборов.

Значения схожи для каждой из трех переменных, что объясняет, почему эти наблюдения так близки друг к другу на биграфике.

В таблице результатов под названием «Собственные значения корреляционной матрицы» мы также увидели, что на первые два главных компонента приходится 88,21% от общего изменения в наборе данных.

Поскольку этот процент очень высок, имеет смысл проанализировать, какие наблюдения на двойном графике близки друг к другу, поскольку два основных компонента, составляющих двойный график, отвечают почти за все изменения в наборе данных.

Дополнительные ресурсы

В следующих руководствах объясняется, как выполнять другие распространенные задачи в SAS:

Как выполнить простую линейную регрессию в SAS
Как выполнить множественную линейную регрессию в SAS
Как выполнить логистическую регрессию в SAS