Как читать таблицу распределения хи-квадрат
В этом руководстве объясняется, как читать и интерпретировать диаграмму распределения Хи-квадрат.
Что такое таблица распределения хи-квадрат?
Таблица распределения хи-квадрат представляет собой таблицу, в которой показаны критические значения распределения хи-квадрат. Чтобы использовать таблицу распределения Хи-квадрат, вам нужно знать всего два значения:
- Степени свободы для теста Хи-квадрат
- Альфа-уровень теста (обычно выбираются 0,01, 0,05 и 0,10).
На следующем изображении показаны первые 20 строк таблицы распределения хи-квадрат со степенями свободы в левой части таблицы и альфа-уровнями в верхней части таблицы:
Примечание. Полную таблицу распределения хи-квадрат с большим количеством степеней свободы можно найти здесь.
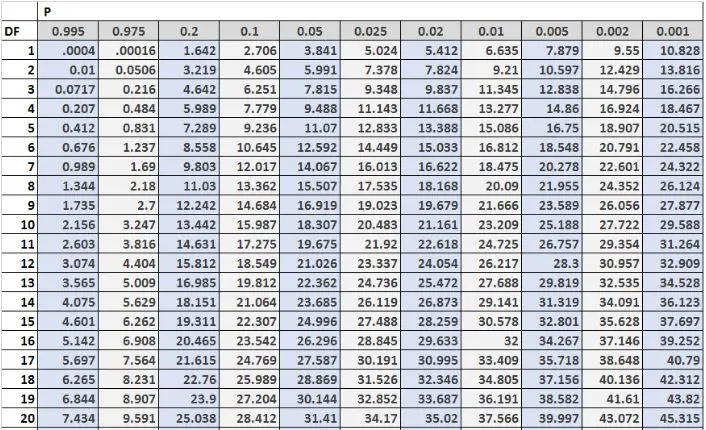
Критические значения в таблице часто сравнивают со статистикой теста хи-квадрат. Если статистика теста превышает критическое значение, указанное в таблице, то вы можете отвергнуть нулевую гипотезу теста хи-квадрат и сделать вывод, что результаты теста статистически значимы.
Примеры использования таблицы распределения хи-квадрат
Мы покажем, как использовать таблицу распределения хи-квадрат со следующими тремя типами тестов хи-квадрат:
- Критерий хи-квадрат на независимость
- Критерий хи-квадрат на предмет согласия
- Критерий хи-квадрат на однородность
Критерий хи-квадрат на независимость
Мы используем критерий Хи-квадрат для определения независимости , когда хотим проверить, существует ли значимая связь между двумя категориальными переменными.
Пример: Предположим, мы хотим знать, связан ли пол с предпочтением той или иной политической партии. Мы берем простую случайную выборку из 500 избирателей и спрашиваем их об их предпочтениях в отношении политических партий. Используя уровень значимости 0,05, мы проводим тест хи-квадрат, чтобы определить, связан ли пол с предпочтениями политических партий. В следующей таблице представлены результаты опроса:
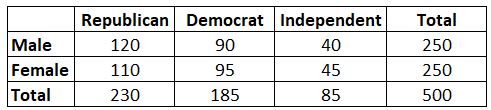
Оказывается, статистика для этого теста хи-квадрат равна 0,864.
Затем мы можем найти критическое тестовое значение в таблице распределения хи-квадрат. Степени свободы равны (#rows-1) * (#columns-1) = (2-1) * (3-1) = 2, и задача подсказывала нам, что мы должны использовать альфа-уровень 0,05. Итак, согласно таблице распределения Хи-квадрат критическое значение теста составляет 5,991 .

Поскольку наша тестовая статистика меньше критического значения, мы не можем отвергнуть нулевую гипотезу. Это означает, что у нас нет достаточных доказательств, чтобы утверждать, что существует связь между полом и предпочтениями политических партий.
Критерий хи-квадрат на предмет согласия
Мы используем критерий согласия хи-квадрат, когда хотим проверить, соответствует ли категориальная переменная гипотетическому распределению.
Пример: Владелец магазина говорит, что 30% всех его покупателей на выходных приходят в пятницу, 50% в субботу и 20% в воскресенье. Независимый исследователь посещает магазин в случайные выходные и находит 91 покупателя в пятницу, 104 в субботу и 65 в воскресенье. Используя уровень значимости 0,10, мы проводим тест хи-квадрат, чтобы проверить соответствие данных и определить, соответствуют ли данные утверждению владельца магазина.
В этом случае тестовая статистика оказывается равной 10 616.
Затем мы можем найти критическое тестовое значение в таблице распределения хи-квадрат. Степени свободы равны (#outcomes-1) = 3-1 = 2, и задача подсказывает нам, что нам следует использовать альфа-уровень 0,10. Итак, согласно таблице распределения Хи-квадрат критическое значение теста составляет 4,605 .
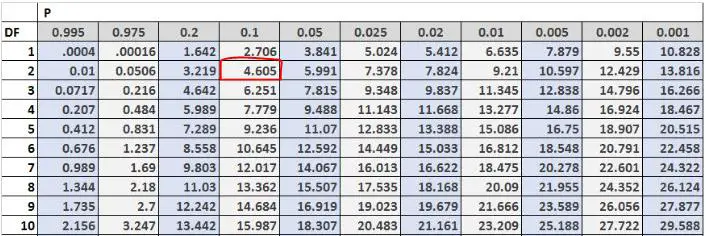
Поскольку наша тестовая статистика превышает наше критическое значение, мы отвергаем нулевую гипотезу. Это означает, что у нас есть достаточно доказательств, чтобы сказать, что истинное распределение покупателей, пришедших в этот магазин в выходные дни, не равно 30% в пятницу, 50% в субботу и 20% в воскресенье.
Критерий хи-квадрат на однородность
Мы используем критерий хи-квадрат на однородность , когда хотим формально проверить, существует ли разница в пропорциях между несколькими группами.
Пример: Баскетбольный тренировочный центр хочет проверить, увеличат ли две новые тренировочные программы долю его игроков, успешно сдающих сложные испытания по стрельбе. 172 игрока случайным образом попадают в программу 1, 173 — в программу 2 и 215 — в текущую программу. После использования тренировочных программ в течение месяца игроки сдают тест по стрельбе. В таблице ниже показано количество игроков, прошедших тест по стрельбе, в зависимости от используемой ими программы.

Используя уровень значимости 0,05, мы проводим тест хи-квадрат, чтобы определить, одинаков ли уровень успеха для каждой программы обучения.
Оказывается, статистика для этого теста хи-квадрат равна 4,208.
Затем мы можем найти критическое тестовое значение в таблице распределения хи-квадрат. Степени свободы равны (#rows-1) * (#columns-1) = (2-1) * (3-1) = 2, и задача подсказывала нам, что мы должны использовать альфа-уровень 0,05. Итак, согласно таблице распределения Хи-квадрат критическое значение теста составляет 5,991 .

Поскольку наша тестовая статистика меньше критического значения, мы не можем отвергнуть нулевую гипотезу. Это означает, что у нас нет достаточных доказательств, чтобы утверждать, что три программы обучения дают разные результаты.