Квинтили (статистика)

В этой статье мы объясним, что такое квинтили и как они рассчитываются. Вы найдете несколько решенных примеров расчета квинтилей и, кроме того, сможете посчитать квинтили любой статистической выборки с помощью онлайн-калькулятора.

Что такое квинтили?

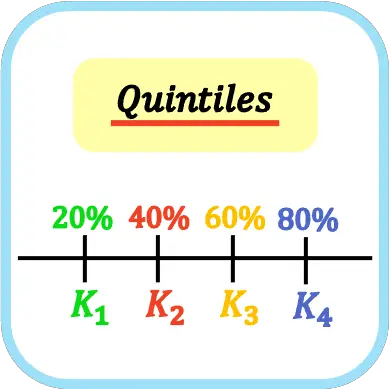
В статистике квинтилями называют четыре значения, делящие набор данных на пять равных частей. Таким образом, первый, второй, третий и четвертый квинтили представляют 20%, 40%, 60% и 80% выборочных данных соответственно.

То есть значение третьего квинтиля, например, выше 60% всех собранных данных, но ниже остальных данных.

Обозначением квинтилей является заглавная буква К с индексом квинтиля, т.е. первый квинтиль — К ₁ , второй квинтиль — К ₂ , третий квинтиль — К ₃ и четвертый квинтиль — К ₄ . Хотя его также можно обозначать буквой Q (не рекомендуется, поскольку это приводит к путанице с квартилями).

👉 Вы можете использовать калькулятор ниже, чтобы рассчитать квинтили для любого набора данных.

Квинтили — это мера нецентрального положения наряду с квартилями, децилями и процентилями. Если вам интересно, вы можете проверить, что означает каждый из этих типов квантилей, на нашем сайте.

Следует отметить, что квинтиль может иметь и другое определение. В экономике квинтили представляют собой процент населения, упорядоченный по доходам, или, другими словами, они ранжируют население по уровням доходов. Например, первый квинтиль соответствует 20% беднейших слоев населения, второй квинтиль соответствует 40% населения с самым низким доходом и так далее.

Как рассчитать квинтили

Чтобы вычислить положение квинтилей выборки или статистической совокупности, необходимо умножить количество квинтилей на сумму общего количества данных плюс один и разделить результат на пять.

Следовательно, формула квинтилей выглядит так:

Обратите внимание: результат этой формулы сообщает нам положение квинтиля, а не его значение. Таким образом, квинтилем будут данные, расположенные в позиции, полученной по формуле.

Однако иногда результат этой формулы дает нам десятичное число, поэтому мы должны различать два случая в зависимости от того, является ли результат десятичным числом или нет:

• Если результатом формулы является число без десятичной части , квинтилем являются данные, расположенные в позиции, указанной в формуле выше.
• Если результатом формулы является число с десятичной частью , значение квинтиля рассчитывается с помощью следующего выражения:

Где x _i и x _i+1 — номера позиций, между которыми находится число, полученное по первой формуле, а d — десятичная часть числа, полученного по первой формуле.

Если вы испугались, увидев так много шагов по определению квинтилей набора данных, не волнуйтесь, на самом деле это довольно просто. Прочитайте следующие два примера, и вы наверняка поймете гораздо лучше.

Примечание . В статистическом сообществе до сих пор нет единого мнения о том, как рассчитываются квинтили, поэтому вы можете найти книгу, в которой это объясняется немного по-другому.

Примеры расчета квинтилей

Ниже мы оставляем вам два пошагово решенных упражнения о том, как получить квинтили из ряда данных. Итак, вы можете увидеть два возможных случая: в первом упражнении результаты не десятичные, а во втором — десятичные.

Пример 1

• Рассчитайте квинтили следующего ряда данных:

Как вы видели в объяснении выше, формула для определения положения квинтилей такова:

Параметр n относится к общему количеству данных, которое равно 49, поэтому, чтобы найти положение первого квинтиля, нам нужно заменить n на 49, а k на 1:

Из формулы мы получили число 10, что означает, что квинтиль находится на десятой позиции упорядоченного списка, что соответствует данным 205.

Для расчета второго квинтиля необходимо использовать ту же формулу, но с заменой k на 2:

Таким образом, второй квинтиль находится на позиции 20 упорядоченного списка, то есть на значении 236.

Снова мы повторяем процесс для определения квинтиля 3, но, по логике вещей, теперь мы заменяем k на 3:

Таким образом, третий квинтиль — это данные, расположенные в позиции 30, что соответствует 266.

Наконец, мы снова применим формулу для расчета четвертого квинтиля:

Таким образом, четвертый квинтиль находится на позиции 40, поэтому четвертый квинтиль равен 286.

Пример 2

• Рассчитайте четыре квинтиля статистических данных, собранных в следующей таблице:

Так же, как и в предыдущем примере, для получения позиций квинтилей необходимо использовать следующую формулу:

В этом случае размер выборки составляет 42 наблюдения, поэтому, чтобы найти положение первого квинтиля, нам нужно заменить параметр n на 42, а k на 1:

Однако, в отличие от первого примера, на этот раз формула дает нам десятичное число, поэтому нам нужно применить следующую формулу для расчета точного квинтиля:

Число, полученное по первой формуле, равно 8,6, поэтому первый квинтиль находится между восьмым и девятым данными, которые равны 78 и 79 соответственно. Следовательно, x _i равно 78, x _i+1 равно 79, а d представляет собой десятичную часть полученного числа, т. е. 0,6.

Теперь мы проделаем ту же самую процедуру еще раз, чтобы найти второй квинтиль. Сначала вычисляем его положение:

Но из формулы мы получаем десятичное число между 17 и 18, так что второй квинтиль окажется между семнадцатой и восемнадцатой позициями, значения которых соответствуют соответственно 109 и 112 упорядоченного списка. Поэтому в процессе применяем вторую формулу для определения точного значения квинтиля:

Повторяем метод получения третьего квинтиля, сначала определяем его положение:

Вычисленное число 25,8 означает, что значение квинтиля будет между двадцать пятой и двадцать шестой позицией, значения которых равны 134 и 141. Таким образом, расчет точного значения квинтиля таков:

Наконец, мы повторяем ту же процедуру в последний раз, чтобы вычислить квинтиль 4. Сначала мы находим его положение:

Таким образом, точное значение четвертого квинтиля будет между 34 и 35, позиции которого соответствуют данным 172 и 179. Таким образом, расчет четвертого квинтиля будет следующим:

Калькулятор квинтиля

Введите набор статистических данных в следующий калькулятор, чтобы рассчитать квинтили. Данные должны быть разделены пробелом и введены с использованием точки в качестве десятичного разделителя.

Квинтили в сгруппированных данных

Чтобы рассчитать квинтили, когда данные сгруппированы в интервалы, необходимо сначала найти его интервал или класс, используя следующую формулу:

Таким образом, квинтиль будет находиться в интервале, абсолютная частота которого сразу больше числа, полученного с помощью предыдущего выражения.

И как только мы узнаем интервал, к которому принадлежит квинтиль, мы должны применить следующую формулу, чтобы найти точное значение квинтиля:

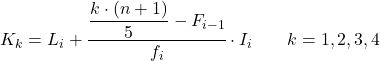
Золото:

• _Li – нижняя граница интервала, в котором находится квинтиль.
• n — общее количество наблюдений.
• F _i-1 представляет собой совокупную абсолютную частоту предыдущего интервала.
• f _i — абсолютная частота интервала, в котором находится квинтиль.
• I _i – ширина квинтильного интервала.

Итак, вы можете увидеть, как это делается, вот решенный пример расчета квинтилей следующих рядов данных, сгруппированных по интервалам:

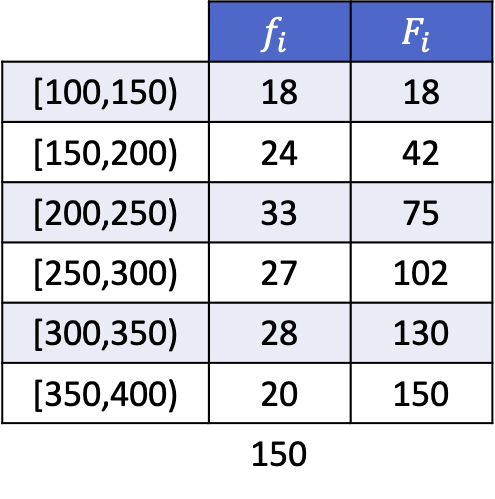
Поскольку данные сгруппированы, для расчета квинтилей необходимо использовать следующий метод: сначала определить диапазон, в который попадает квинтиль, затем найти точное значение квинтиля.

Таким образом, чтобы найти интервал, в котором находится первый квинтиль, воспользуемся следующей формулой:

Первый квинтиль будет находиться в интервале, чья совокупная абсолютная частота сразу превышает 30,2, в данном случае это интервал [150,200), чья совокупная абсолютная частота равна 42. И как только мы узнаем интервал квинтиля, мы применим вторую формулу процесс для определения его точного значения:

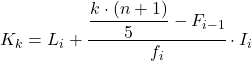
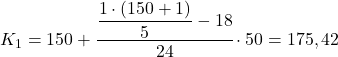
Теперь повторяем ту же процедуру для получения второго квинтиля, предварительно рассчитав интервал, в котором он находится:

Совокупная абсолютная частота непосредственно выше 60,4 равна 75, поэтому второй квинтильный диапазон составляет [200–250). Поэтому подставляем соответствующие значения во вторую формулу для расчета точного значения квинтиля:

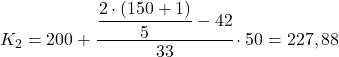
Проделываем ту же процедуру в третий раз, чтобы получить квинтиль 3. Сначала определяем интервал, в котором находится квинтиль:

Квинтиль находится в интервале [250,300), потому что его совокупная абсолютная частота (102) находится непосредственно над 90,6. Таким образом, расчет точного значения третьего квинтиля выглядит следующим образом:

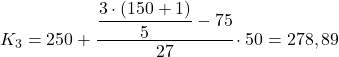
Наконец, мы найдем четвертый квинтиль. Как всегда, сначала находим его интервал:

Интервал, абсолютная частота которого сразу превышает 120,8, равен [300,350), значение которого равно 130. Таким образом, точное значение четвертого квинтиля будет: