Заговор с коробкой и усами

К бенджамин андерсон 5 августа, 2023 Статистика 0 комментариев

В этой статье объясняется, что такое коробчатая диаграмма, также известная как коробчатая диаграмма (или коробчатая диаграмма). Вы узнаете, как создаются статистические диаграммы такого типа, а также решите упражнение с диаграммой «ящик с усами» и ее интерпретацию.

Что такое сюжет «коробка и усы»?

Boxplot , также называемый boxplot или boxplot , представляет собой график, который визуально представляет набор статистических данных с использованием квартилей.

Основная характеристика диаграммы «ящик с усами» заключается в том, что она позволяет быстро визуализировать дисперсию ряда данных, поскольку указывает квартили, медиану, экстремальные значения и выбросы данных.

Таким образом, этот тип диаграммы состоит из прямоугольной рамки и нескольких линий (или усов), из которых появляются следующие значения:

Границы прямоугольника обозначают первый и третий квартили (Q ₁ и Q ₃ ). А вертикальная линия внутри рамки — это медиана (эквивалент второго квартиля _Q2 ).
Пределы усов (или плеч) — это крайние значения , то есть минимальное и максимальное значения ряда данных.
Точки за пределами усов — это выбросы , или, другими словами, данные, которые, вероятно, были измерены неправильно и поэтому не должны учитываться в статистическом исследовании.

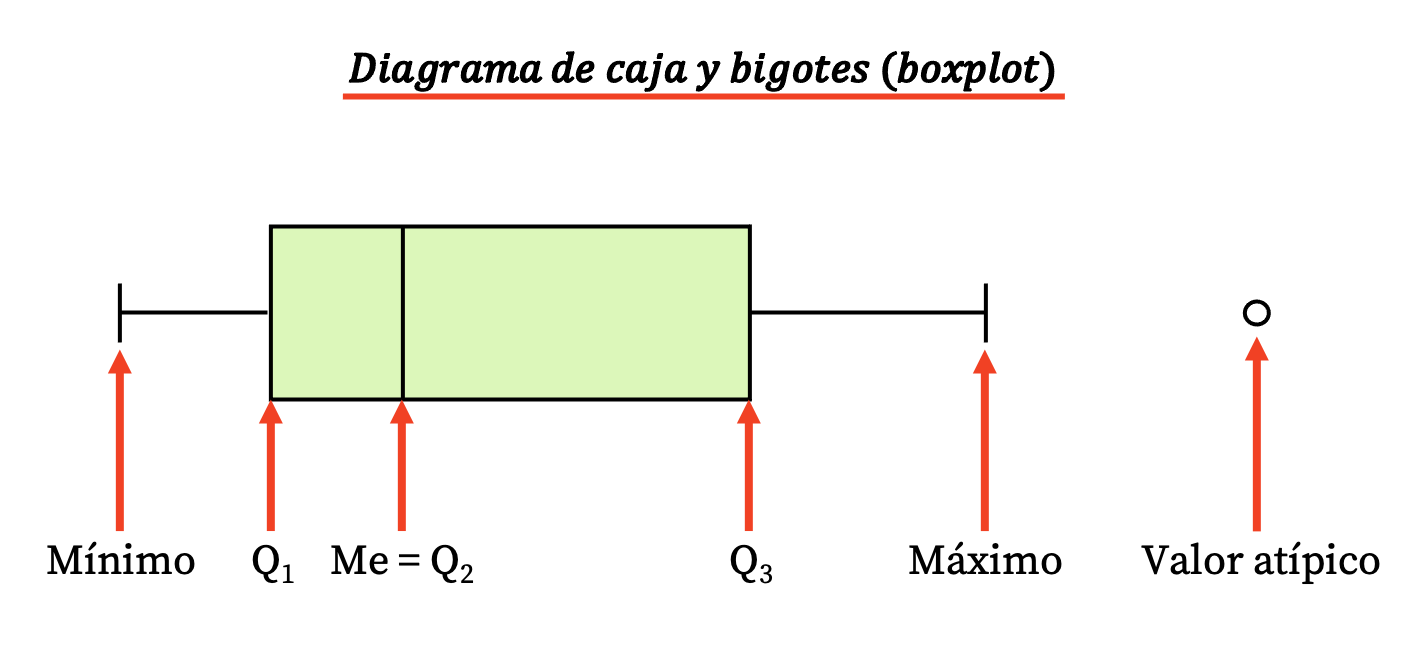
Обратите внимание, что разница между третьим и первым квартилем представляет собой межквартильный размах (или межквартильный размах), еще один показатель статистической дисперсии.

Диаграммы «ящик» и «усы» очень полезны для сравнения числовых переменных. Однако он не подходит для представления категориальных переменных.

Как создать прямоугольник и диаграмму с усами

Чтобы создать диаграмму с усами (или коробчатую диаграмму) из ряда данных, необходимо выполнить следующие шаги:

Разобрать примеры статистических данных.
Вычислите квартили (Q ₁ , Q ₂ и Q ₃ ) и изобразите их в виде прямоугольника на диаграмме. Первый и третий квартиль соответствуют границам поля, и для обозначения медианы (второго квартиля) необходимо провести линию внутри поля, где находится его значение.
Рассчитайте межквартильный размах, который равен третьему квартилю минус первый квартиль.

$IQR=Q_3-Q_1$

Рассчитайте допустимые значения LI и LS, формулы которых:

$LI=Q_1-1,5\cdot IQR$

$LS=Q_3+1,5\cdot IQR$

Определите выборочные выбросы, которые имеют значения меньше LI или больше LS. Обозначьте эти значения за пределами диапазона «усов» точками.
Определите и представьте экстремальные значения, которые представляют собой наименьшее значение и наибольшее значение в интервале, образованном LI и LS. Эти значения представляют собой конец двух усов на диаграмме.

Пример графика «Коробка и усы»

Рассматривая определение и теорию диаграммы «ящик и усы» (или диаграмму «ящик»), ниже вы найдете конкретный пример, который поможет лучше понять концепцию и увидеть, как выполняется этот тип статистического графика.

Нарисуйте коробчатую диаграмму следующего набора статистических данных.

В этом случае данные уже упорядочены от меньшего к большему, поэтому никаких изменений не требуется. В противном случае нам следует сначала отсортировать образцы данных.

Во-вторых, мы извлекаем квартили выборки:

$Q_1=4,06$

$Q_2=4,38$

$Q_3=4,66$

➤ См.: Калькулятор квартилей

После того, как мы вычислили три квартиля, мы находим межквартильный размах, вычитая квартиль 3 минус квартиль 1:

$IQR=Q_3-Q_1=4,66-4,06=0,6$

Теперь рассчитаем пределы LI и LS — значения, начиная с которых данные считаются нетипичными. Для этого необходимо использовать следующие формулы:

$LI=Q_1-1,5\cdot IQR=4,06-1,5\cdot 0,6=3,16$

$LS=Q_3+1,5\cdot IQR=4,66+1,5\cdot 0,6=5,56$

Итак, в этом случае у нас есть два выброса, потому что 3,02 меньше 3,16, а 5,71 больше 5,56.

$\text{Valores at\'ipicos} =\Bigl\{3,02 \ ; \ 5,71\Bigr\}$

Наконец, осталось выявить крайние значения, которые являются минимумом и максимумом всех данных, находящихся в интервале [LI,LS]. Поэтому в нашем примере минимальное значение составляет 3,70, а максимальное значение — 4,81.

$\text{M\'inimo}=3,70$

$\text{M\'aximo}=4,81$

Итак, как только мы определили все значения прямоугольника и усового графика, остается только сделать графическое представление:

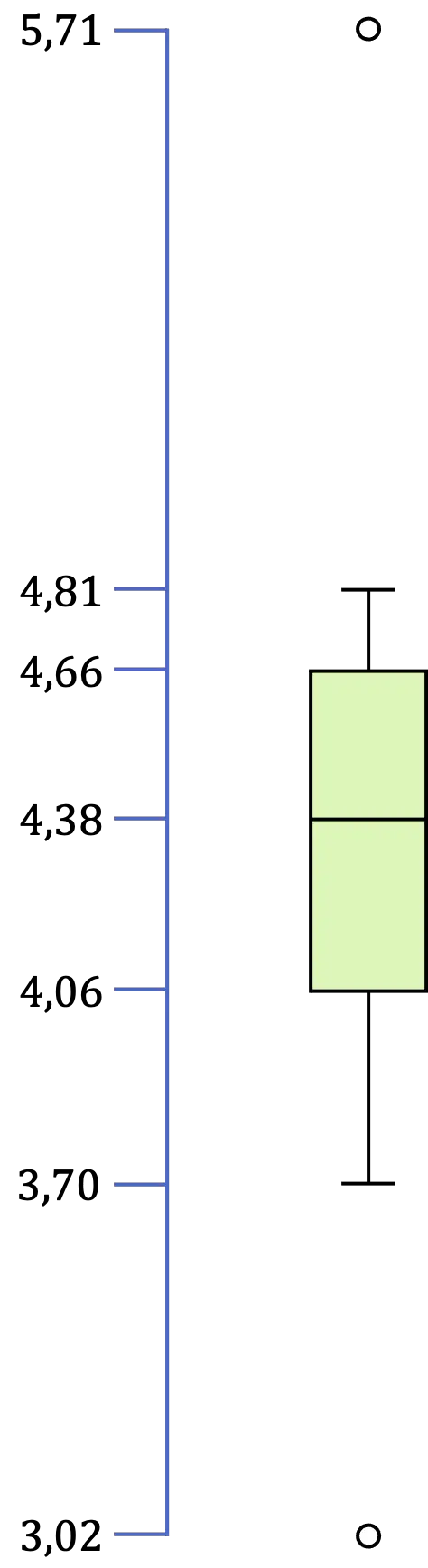
Для чего используется диаграмма «ящик и усы»?

Наконец, давайте посмотрим, для чего он нужен и как интерпретировать диаграмму «ящик с усами» (или коробчатую диаграмму).

Очевидно, что диаграмма «ящик с усами» очень полезна для быстрого определения квартилей, межквартильного диапазона, медианы, экстремальных значений и выбросов ряда данных, поскольку все эти статистические показатели можно идентифицировать с помощью простого просмотра.

Кроме того, диаграмма «ящик с усами» используется для анализа симметрии статистической выборки, поскольку она визуально представляет весь набор данных. Если медиана не находится в центре поля, это означает, что выборка не симметрична.

Точно так же коробчатые диаграммы широко используются на фондовом рынке для представления изменений цены акции за определенный период времени, поскольку они позволяют увидеть максимальное значение, минимальное значение и промежуточные значения за короткий период времени. время и, таким образом, быстрее принимать решения.

Об авторе

бенджамин андерсон

Здравствуйте, я Бенджамин, профессор статистики на пенсии, ставший преданным преподавателем Statorials. Имея обширный опыт и знания в области статистики, я хочу поделиться своими знаниями, чтобы расширить возможности студентов с помощью Statorials. Узнать больше