Средняя разница

К бенджамин андерсон 5 августа, 2023 Статистика 0 комментариев

В этой статье объясняется, что такое среднее отклонение и как оно рассчитывается. Вы также найдете конкретные примеры расчета среднего отклонения. И, более того, вы сможете посчитать среднее отклонение любого набора статистических данных с помощью онлайн-калькулятора.

Что такое среднее отклонение?

Среднее отклонение , также называемое средним абсолютным отклонением , является мерой статистической дисперсии.

Среднее отклонение набора данных — это среднее абсолютных отклонений . Следовательно, среднее отклонение равно сумме отклонений каждого элемента данных от среднего арифметического, деленной на общее количество элементов данных.

Другими словами, формула среднего отклонения выглядит следующим образом:

👉 Вы можете использовать калькулятор ниже, чтобы рассчитать среднее отклонение любого набора данных.

В статистике среднее отклонение также называют средним абсолютным отклонением .

Интерпретация среднего отклонения производится следующим образом: чем больше значение среднего отклонения, это означает, что данные находятся в среднем дальше от среднего арифметического; и наоборот, чем ниже среднее отклонение, тем ближе значение. данные есть. Таким образом, среднее отклонение указывает на дисперсию ряда данных.

Другими мерами, считающимися распределенными, являются диапазон, межквартильный диапазон, стандартное отклонение (или стандартное отклонение), дисперсия и коэффициент вариации.

Как рассчитать среднее отклонение

Чтобы рассчитать среднее отклонение ряда данных, необходимо выполнить следующие шаги:

Вычислите среднее арифметическое набора статистических данных.
Рассчитайте отклонение каждой точки данных от среднего значения, определяемое как абсолютное значение разницы между данными и средним значением.
Сложите все разницы, рассчитанные на предыдущем шаге.
Разделите на общее количество данных. Полученный результат представляет собой среднее отклонение ряда данных.

Вкратце, формула, которую необходимо применить для нахождения среднего отклонения, выглядит следующим образом:

$D_{\overline{x}}=\cfrac{\sum_{i=1}^N|x_i-\overline{x}|}{N}$

Пример расчета среднего отклонения

Учитывая определение среднего отклонения, ниже приведен пошаговый пример расчета среднего отклонения статистической выборки. Так вы лучше поймете, как получить среднее отклонение.

Аналитик изучает экономические результаты компании за прошедший год и располагает информацией о прибыли, полученной компанией за каждый квартал указанного года: 2, 3, 7 и 5 миллионов долларов. Каково среднее отклонение данных?

Сначала нам нужно усреднить данные, поэтому суммируем и делим на общее количество наблюдений (4):

$\overline{x}=\cfrac{2+3+7+5}{4}=4,25$

После того, как мы вычислили среднее арифметическое, воспользуемся формулой среднего отклонения:

$D_{\overline{x}}=\cfrac{\sum_{i=1}^N|x_i-\overline{x}|}{N}$

Подставляем данные в формулу:

$D_{\overline{x}}=\cfrac{|2-4,25|+|3-4,25|+|7-4,25|+|5-4,25|}{4}$

Делаем вычисления в числителе:

$D_{\overline{x}}=\cfrac{|-2,25|+|-1,25|+|2,75|+|0,75|}{4}$

$D_{\overline{x}}=\cfrac{2,25+1,25+2,75+0,75}{4}$

$D_{\overline{x}}=\cfrac{7}{4}$

И наконец, делим на общее количество данных, чтобы получить среднее отклонение выборки:

$D_{\overline{x}}=1,75$

Калькулятор среднего отклонения

Введите набор статистических данных в следующий калькулятор, чтобы рассчитать его среднее отклонение. Данные должны быть разделены пробелом и введены с использованием точки в качестве десятичного разделителя.

Среднее отклонение для сгруппированных данных

Для расчета среднего отклонения данных, сгруппированных по интервалам, необходимо выполнить следующие шаги:

Определите среднее арифметическое набора статистических данных. Поскольку данные сгруппированы, выражение для расчета среднего значения имеет следующий вид:

$\overline{x}=\cfrac{\sum_{i=1}^N x_i\cdot f_i}{N}$

Рассчитайте отклонение каждого интервала от среднего значения, которое эквивалентно абсолютному значению разницы между оценкой класса и средним значением.

$|x_i-\overline{x}|$

Умножьте отклонение каждого интервала на его абсолютную частоту.

$|x_i-\overline{x}|\cdot f_i$

Сложите все результаты предыдущего шага, затем разделите на общее количество данных. Полученный результат представляет собой среднее отклонение выборки, сгруппированной по интервалам.

$\cfrac{\sum_{i=1}^N|x_i-\overline{x}|\cdot f_i}{N}$

В заключение формула для получения среднего отклонения от сгруппированных данных имеет вид:

$D_{\overline{x}}=\cfrac{\sum_{i=1}^N|x_i-\overline{x}|\cdot f_i}{N}$

Когда данные сгруппированы, это обычно означает, что данных много, и поиск среднего отклонения включает в себя множество шагов. Поэтому для выполнения расчета обычно используют таблицы частот.

Ниже приведено пошаговое упражнение по расчету среднего отклонения, когда данные сгруппированы по интервалам:

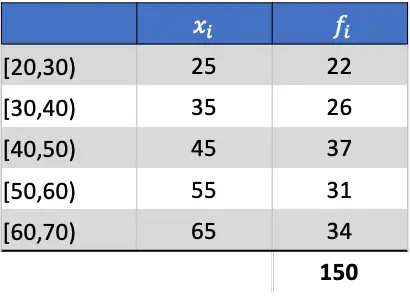
Первое, что нужно сделать, это вычислить среднее значение сгруппированных данных. Для этого добавим столбец в таблицу, умножив классную заметку на ее частоту:

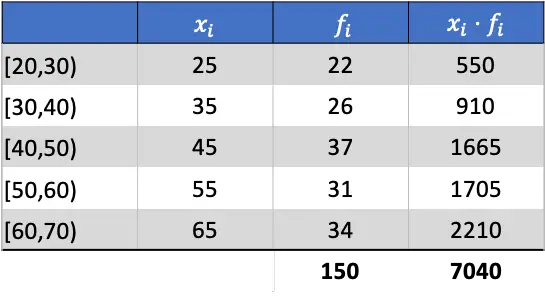
Таким образом, среднее арифметическое будет результатом деления суммы добавленного столбца на сумму абсолютных частот:

$\overline{x}=\cfrac{\sum_{i=1}^N x_i\cdot f_i}{N}=\cfrac{7040}{150}=46,93$

Теперь, когда мы знаем среднее значение данных, мы можем добавить все необходимые столбцы, чтобы найти среднее отклонение:

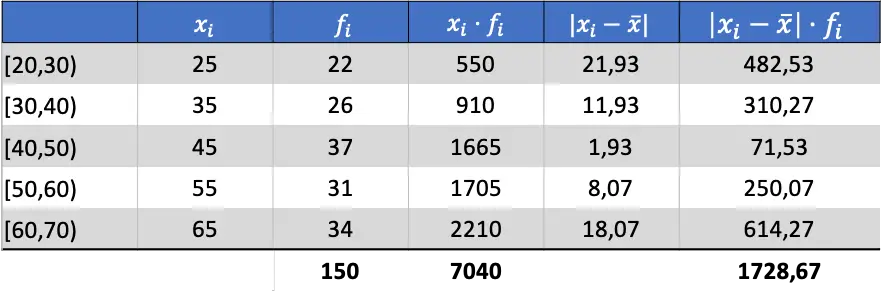
Таким образом, чтобы получить среднее отклонение необходимо разделить сумму последнего столбца на общее количество наблюдений:

$D_{\overline{x}}=\cfrac{\sum_{i=1}^N|x_i-\overline{x}|\cdot f_i}{N}=\cfrac{1728,67}{150}=11,52$

Об авторе

бенджамин андерсон

Здравствуйте, я Бенджамин, профессор статистики на пенсии, ставший преданным преподавателем Statorials. Имея обширный опыт и знания в области статистики, я хочу поделиться своими знаниями, чтобы расширить возможности студентов с помощью Statorials. Узнать больше