Ковариация
В этой статье объясняется, что такое ковариация и как она рассчитывается. Вы найдете формулу ковариации, а также пример расчета ковариации набора данных. Кроме того, вы можете рассчитать ковариацию любого ряда данных с помощью онлайн-калькулятора в конце.
Что такое ковариация?
В статистике ковариация — это величина, указывающая степень совместного изменения двух случайных величин. Другими словами, ковариация используется для анализа зависимости между двумя переменными.
Ковариация равна сумме произведений разностей между данными двух переменных и их соответствующими средними значениями, разделенной на общее количество данных.

👉 Вы можете использовать калькулятор ниже, чтобы рассчитать ковариацию любого набора данных.
Интерпретация значения ковариации очень проста:
- Если ковариация положительна , это означает, что между двумя переменными существует зависимость. Следовательно, когда значение одной переменной увеличивается, другая переменная также увеличивается, и наоборот.
- Если ковариация отрицательна , это означает, что связь между двумя переменными отрицательна. Таким образом, когда значение одной переменной увеличивается, значение другой переменной уменьшается, и наоборот.
- Если ковариация равна нулю (или ее значение близко к нулю), это означает, что между двумя переменными нет связи. Другими словами, две случайные величины независимы.
Как рассчитать ковариацию
Чтобы вычислить ковариацию ряда данных, необходимо выполнить следующие шаги:
- Рассчитайте среднее значение каждой переменной отдельно.
- Для каждой переменной найдите разницу между каждым из ее значений и средним значением переменной.
- Умножьте разницы, рассчитанные на предыдущем шаге, для каждой точки данных.
- Сложите все результаты, полученные на предыдущем шаге.
- Разделите на общее количество данных. Полученное значение является ковариацией ряда данных.
Вкратце, формула для расчета ковариации между двумя переменными выглядит следующим образом:
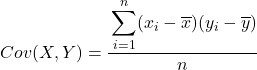
Настоятельно рекомендуемый метод извлечения ковариации между двумя переменными — создать таблицу со всеми парами данных и добавить столбец для каждого из шагов, описанных выше. Таким образом, ваши расчеты будут намного лучше организованы, и вы лучше поймете, что делаете.
Пример расчета ковариации
Что касается определения ковариации, ниже приведен пошаговый пример расчета этого типа статистической меры. Цель состоит в том, чтобы вы лучше поняли концепцию ковариации и способы анализа корреляции между двумя переменными.
- Рассчитайте ковариацию следующего набора статистических данных:

Сначала нам нужно вычислить среднее арифметическое каждой переменной. Для этого делим сумму значений каждой переменной на общее количество данных.
![]()
![]()
Как только мы определим среднее значение каждой случайной величины, мы можем добавить следующие столбцы в таблицу данных, чтобы получить ковариацию:
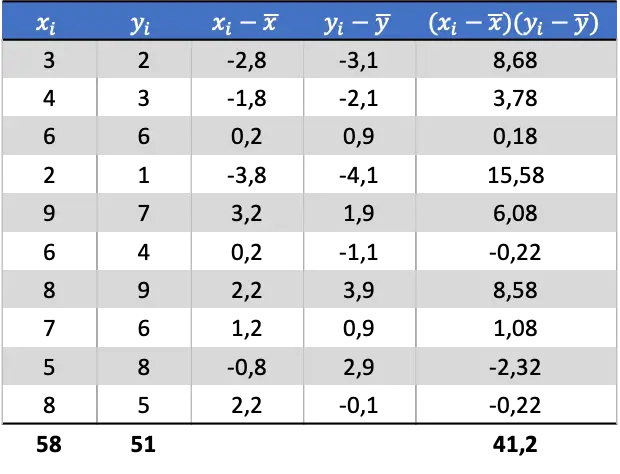
Итак, чтобы определить ковариацию двух переменных, вы должны разделить сумму последнего столбца на количество пар данных:
![Rendered by QuickLaTeX.com \begin{aligned}Cov(X,Y)&=\cfrac{\displaystyle \sum_{i=1}^n (x_i-\overline{x})(y_i-\overline{y})}{n}\\[2ex] Cov(X,Y)&= \cfrac{41,2}{10} \\[2ex]Cov(X,Y)&= 4,12\end{aligned}](https://statorials.org/wp-content/ql-cache/quicklatex.com-49b4992f8443e4d94e38dfa56da38a9a_l3.png)
В этом случае значение ковариации положительное, что означает наличие прямой зависимости между двумя изучаемыми случайными величинами. Однако если бы значение ковариации было отрицательным, это означало бы, что зависимость между двумя переменными обратная. И, наконец, если значение ковариации равно нулю или очень близко к нулю, это означает, что между двумя переменными нет линейной зависимости.
Как видно из решения этого примера, очень полезно использовать компьютерную программу, например Excel, для добавления столбцов в таблицу и быстрого выполнения вычислений. В противном случае, вычисляя операции вручную, поиск ковариации займет гораздо больше времени.
Калькулятор ковариации
Введите набор статистических данных в следующий калькулятор, чтобы рассчитать ковариацию между двумя переменными. Вам нужно разделить пары данных так, чтобы в первом поле были только значения одной переменной, а во втором поле — только значения второй переменной.
Данные должны быть разделены пробелом и введены с использованием точки в качестве десятичного разделителя.
Ковариационные свойства
Ковариация обладает следующими свойствами:
- Ковариация между случайной величиной и константой равна нулю.
![]()
- Ковариация переменной и сама по себе эквивалентна дисперсии этой переменной.
![]()
- Ковариация удовлетворяет свойству симметрии, поэтому ковариация переменных X и Y равна ковариации переменных Y и X. Порядок переменных не влияет на результат ковариации.
![]()
- Если переменные умножаются на константы, вы можете сначала вычислить ковариацию, а затем умножить результат на константы.
![]()
- Добавление членов к переменным не влияет на результат ковариации.
![]()
- Ковариация между двумя случайными величинами связана с их математическими ожиданиями. Ковариация между переменными X и Y равна математическому ожиданию произведения X и Y минус произведение математического ожидания каждой переменной.
![]()
- При работе с переменными по ковариации заполняется следующее алгебраическое выражение:
![Rendered by QuickLaTeX.com \begin{aligned}\displaystyle Cov(aX+bY,cW+dV)= \ & \displaystyle acCov(X,W)+adCov(X,V)+\\[2ex]& +bcCov(Y,W)+bdCov(Y,V)\end{aligned}](https://statorials.org/wp-content/ql-cache/quicklatex.com-5d429b5bb4e4796cc5b8c73ed0845fa2_l3.png)