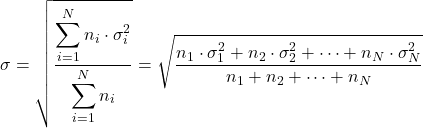Стандартное отклонение (или стандартное отклонение)

К бенджамин андерсон 5 августа, 2023 Статистика 0 комментариев

В этой статье объясняется, что такое стандартное отклонение, также называемое стандартным отклонением. Вы узнаете, как рассчитать стандартное отклонение, получите пошаговый практический пример и онлайн-калькулятор, позволяющий найти стандартное отклонение для любой выборки данных.

Что такое стандартное отклонение (или стандартное отклонение)?

Стандартное отклонение , также называемое стандартным отклонением , является мерой статистической дисперсии. Другими словами, стандартное отклонение — это величина, которая указывает на дисперсию набора статистических данных.

Следовательно, стандартное отклонение (или стандартное отклонение) используется для количественной оценки дисперсии совокупности или статистической выборки. Чем больше стандартное отклонение ряда данных, тем более разбросаны данные. И интерпретацию можно выполнить и в другую сторону: если стандартное отклонение низкое, это означает, что в целом данные очень близки к среднему значению.

При расчете стандартного или типичного отклонения для популяции символом стандартного отклонения является греческая буква сигма (σ). Но когда дело доходит до стандартного отклонения выборки, буква s используется для обозначения статистического измерения.

В некоторых книгах по статистике и вероятностям стандартное отклонение также называют стандартным отклонением.

Формула стандартного отклонения (или стандартного отклонения)

Стандартное отклонение (или стандартное отклонение) равно квадратному корню из суммы квадратов отклонений ряда данных, деленной на общее количество наблюдений.

Таким образом , формула для расчета стандартного отклонения (или стандартного отклонения) :

стандартное отклонение, стандартное отклонение

👉 Вы можете использовать калькулятор ниже, чтобы рассчитать стандартное отклонение любого набора данных.

В заключение, чтобы найти стандартное отклонение набора данных, вам необходимо вычислить все отклонения (определяемые как разница между точкой данных и средним арифметическим), увеличить отклонения до двух, сложить их все, а затем разделить на общий. количество данных и, наконец, извлечь квадратный корень.

Пример стандартного отклонения (или стандартного отклонения)

Учитывая определение стандартного отклонения (или типичного отклонения), ниже приведен пошаговый пример, чтобы вы могли увидеть, как рассчитывается стандартное отклонение ряда данных.

Рассчитайте стандартное отклонение следующих значений: 3, 6, 2, 9, 4.

Первое, что нам нужно сделать, это определить выборочное среднее. Для этого сложим все данные и разделим на общее количество наблюдений, которое равно пяти:

$\overline{x}=\cfrac{3+6+2+9+4}{5}=4,8$

Теперь мы используем формулу стандартного отклонения:

$\displaystyle\sigma=\sqrt{\frac{\displaystyle\sum_{i=1}^N(x_i-\overline{x})^2}{N}}$

Подставляем данные в формулу:

$\displaystyle\sigma =\sqrt{\frac{(3-4,8)^2+(6-4,8)^2+(2-4,8)^2+(9-4,8)^2+(4-4,8)^2}{5}}$

И, наконец, мы вычисляем стандартное отклонение:

$\begin{aligned}\displaystyle\sigma & = \sqrt{\frac{(-1,8)^2+1,2^2+(-2,8)^2+4,2^2+(-0,8)^2}{5}}\\[2ex]&=\sqrt{\frac{3,24+1,44+7,84+17,64+0,64}{5}}\\[2ex]&= \sqrt{\frac{30,8}{5}}=\sqrt{6,16}=2,48 \end{aligned}$

Калькулятор стандартного отклонения (или стандартного отклонения)

Введите набор статистических данных в следующий онлайн-калькулятор, чтобы рассчитать его стандартное отклонение (или стандартное отклонение). Данные должны быть разделены пробелом и введены с использованием точки в качестве десятичного разделителя.

Стандартное (или типичное) отклонение для сгруппированных данных

Чтобы рассчитать стандартное отклонение (или стандартное отклонение) данных, сгруппированных в интервалы , необходимо выполнить следующие шаги:

Найдите среднее значение сгруппированных данных.
Рассчитать отклонения сгруппированных данных.
Выровняйте каждый зазор.
Умножьте каждый предыдущий результат на частоту его интервала.
Сложите сумму всех значений, полученных на предыдущем шаге.
Разделите на общее количество наблюдений.
Возьмите квадратный корень из предыдущего значения. Полученное число представляет собой стандартное отклонение сгруппированных данных.

В заключение формула расчета стандартного отклонения данных, сгруппированных по интервалам:

$\displaystyle\sigma=\sqrt{\frac{\displaystyle\sum_{i=1}^N\left(x_i-\overline{x}\right)^2\cdot f_i }{N}}$

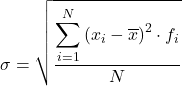
Хотя обычно используется приведенная выше формула, можно также использовать следующее алгебраическое выражение, поскольку получается тот же результат:

$\displaystyle\sigma=\sqrt{\frac{\displaystyle\sum_{i=1}^n x_i^2\cdot f_i }{N}-\overline{x}^2}$

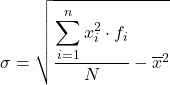
Чтобы вы могли увидеть, как это делается, ниже приведено пошаговое упражнение по определению стандартного отклонения данных, сгруппированных по интервалам. Точнее, будет рассчитано стандартное отклонение следующих статистических данных:

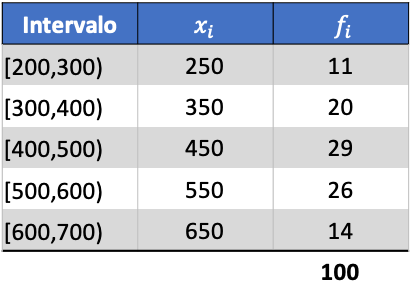
пример данных, сгруппированных по интервалам

Сначала мы умножаем оценку класса каждого интервала на его частоту, чтобы вычислить среднее арифметическое:

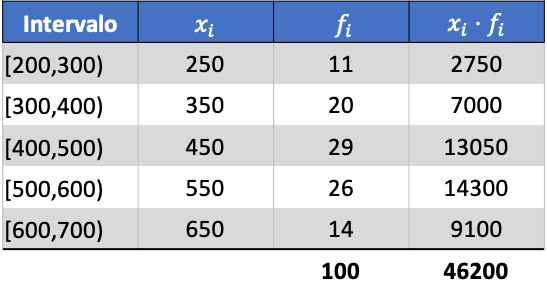
Таким образом, среднее значение сгруппированных данных будет:

$\overline{x}=\cfrac{\displaystyle\sum_{i=1}^n x_i\cdot f_i}{N}=\cfrac{46200}{100}=462$

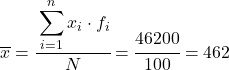
Теперь, когда мы знаем значение среднего значения, нам нужно добавить в таблицу данных следующие три столбца:

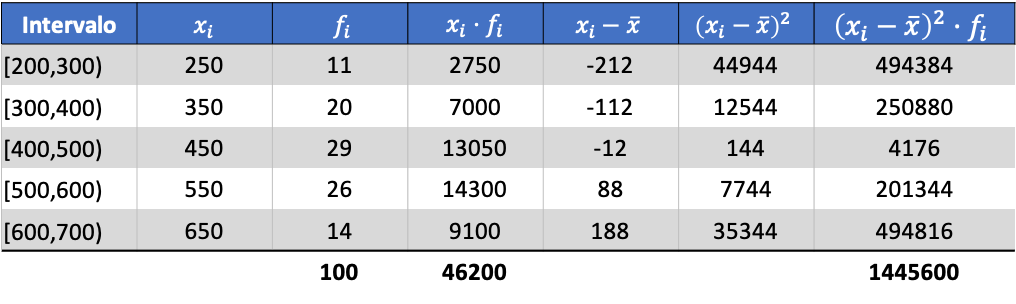
решенное определение стандартного отклонения или стандартного отклонения для сгруппированных данных

Тогда стандартное отклонение сгруппированных данных будет результатом квадратного корня из суммы последнего столбца, разделенной на общее количество наблюдений:

$\displaystyle\sigma=\sqrt{\frac{\displaystyle\sum_{i=1}^N\left(x_i-\overline{x}\right)^2\cdot f_i }{N}}=\sqrt{\frac{1445600}{100}}=120,23$

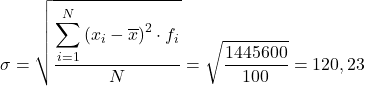
Стандартное (или типичное) отклонение и дисперсия

Связь между стандартным отклонением (или типичным отклонением) и дисперсией заключается в том, что стандартное отклонение представляет собой квадратный корень дисперсии.

Итак, если мы знаем значение дисперсии набора данных, мы можем легко вычислить стандартное отклонение, извлекая квадратный корень. И наоборот, если мы знаем стандартное отклонение, мы можем найти дисперсию, возведя значение в квадрат.

$Var(X)=\sigma^2$

Фактически, дисперсию можно представить просто с помощью символа квадрата стандартного отклонения. Следовательно, символ генеральной дисперсии — это сигма в квадрате (σ ² ), а символ выборочной дисперсии — s в квадрате (s ² ).

Кроме того, концепции стандартного отклонения и дисперсии имеют аналогичную интерпретацию, поскольку оба показывают дисперсию ряда статистических данных.

Свойства стандартного отклонения (или стандартного отклонения)

Стандартное отклонение обладает следующими свойствами:

Стандартное отклонение выборки данных не может быть отрицательным.

$\sigma \ge 0$

Стандартное отклонение будет равно нулю, если все данные одинаковы.

$\sigma =0$

Если ко всем данным добавить постоянный член, значение стандартного отклонения не изменится.

$\sigma (X+k)=\sigma (X)$

Если все данные умножить на число, стандартное отклонение будет умножено на абсолютное значение указанного числа.

$\sigma (k\cdot X)=|k|\cdot \sigma (X)$

Стандартное отклонение суммы двух случайных величин равно квадратному корню из суммы дисперсий переменных плюс удвоенная ковариация между двумя переменными.

$\sigma(X+Y)=\sqrt{Var(X)+Var(Y)+2\cdot Cov(X,Y)}$

Если мы знаем стандартные отклонения различных распределений (σ _i ) и количество их данных ( _ni ), мы можем рассчитать общее стандартное отклонение, применив следующую формулу:

$\displaystyle\sigma=\sqrt{\frac{\displaystyle \sum_{i=1}^N n_i\cdot \sigma_i^2}{\displaystyle \sum_{i=1}^N n_i}}=\sqrt{\frac{\displaystyle n_1\cdot \sigma_1^2+n_2\cdot \sigma_2^2+\dots +n_N\cdot \sigma_N^2}{\displaystyle n_1+n_2+\dots+n_N}}$

Об авторе

бенджамин андерсон

Здравствуйте, я Бенджамин, профессор статистики на пенсии, ставший преданным преподавателем Statorials. Имея обширный опыт и знания в области статистики, я хочу поделиться своими знаниями, чтобы расширить возможности студентов с помощью Statorials. Узнать больше