Как вручную выполнить повторные измерения anova
ANOVA с повторными измерениями используется для определения того, существует ли статистически значимая разница между средними значениями трех или более групп, в которых одни и те же субъекты появляются в каждой группе.
В этом руководстве объясняется, как вручную выполнить однофакторный дисперсионный анализ с повторными измерениями.
Пример: односторонние повторные измерения ANOVA вручную
Исследователи хотят знать, вызывают ли три разных препарата разное время реакции. Чтобы проверить это, они измеряют время реакции (в секундах) пяти пациентов на каждый препарат. Результаты показаны ниже:
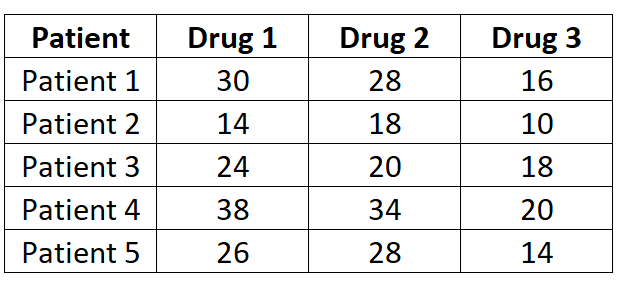
Поскольку у каждого пациента измеряется прием каждого из трех лекарств, мы будем использовать однофакторный дисперсионный анализ с повторными измерениями, чтобы определить, различается ли среднее время реакции между лекарствами.
Выполните следующие шаги, чтобы вручную выполнить повторные измерения ANOVA:
Шаг 1: Рассчитайте SST.
Сначала рассчитаем общую сумму квадратов (SST), которую можно найти по следующей формуле:
SST = s 2 всего (n всего -1)
Золото:
- s 2 total : дисперсия для набора данных
- n total : общее количество наблюдений в наборе данных.
В этом примере мы рассчитываем SST следующим образом: (64,2667)(15-1) = 899,7.
Шаг 2: Рассчитайте SSB
Далее посчитаем сумму квадратов (SSB), которую можно найти по следующей формуле:
SSB = Σn j ( x j – x всего ) 2
Золото:
- Σ : греческий символ, означающий «сумма».
- n j : общее количество наблюдений в j- й группе
- x j : среднее значение j-й группы
- x total : среднее всех данных
В этом примере мы вычисляем SSB следующим образом: (5)(26,4-22,533) 2 +(5)(25,6-22,533) 2 + (5)(15,6-22,533) 2 = 362,1
Шаг 3: Рассчитайте SSS.
Далее рассчитаем сумму квадратов предмета (ССС), которую можно найти по следующей формуле:
SSS =(Σr 2 k /c) – (N 2 /rc)
Золото:
- Σ : греческий символ, означающий «сумма».
- r 2 k : сумма квадратов k-го пациента
- N: общая сумма всех данных
- r: общее количество пациентов
- c: общее количество групп
В этом примере мы вычисляем SSS следующим образом: ((74 2 + 42 2 + 62 2 + 92 2 + 68 2 )/3) – (338 2 /(5)(3)) = 441,1.
Шаг 4: Рассчитайте SES.
Далее мы рассчитаем сумму квадратов ошибок (SSE), которую можно найти по следующей формуле:
SSE = SST – SSB – SSS
В этом примере мы рассчитываем SES следующим образом: 899,7 – 362,1 – 441,1 = 96,5.
Шаг 5: Заполните таблицу ANOVA повторных измерений.
Теперь, когда у нас есть SSB, SSS и SSE, мы можем заполнить таблицу ANOVA с повторными измерениями:
| Источник | Сумма квадратов (СС) | дф | Среднеквадратичные (МС) | Ф |
|---|---|---|---|---|
| Между | 362,1 | 2 | 181,1 | 15.006 |
| Предмет | 441,1 | 4 | 110,3 | |
| Ошибка | 96,5 | 8 | 12.1 |
Вот как мы рассчитали разные числа в таблице:
- df между: #groups – 1 = 3 – 1 = 2
- тема df: #участники – 1 = 5 – 1 = 4
- Ошибка df: df между * df subject = 2*4 = 8
- Входит MS: SSB/df входит = 362,1/2 = 181,1
- Объект MS: субъект SSS / df = 441,1 / 4 = 110,3
- Ошибка MS: ошибка SSE / df = 96,5 / 8 = 12,1
- F: вход MS/ошибка MS = 181,1/12,1 = 15,006
Шаг 6: Интерпретируйте результаты.
Статистика F-теста для этого одностороннего дисперсионного анализа с повторными измерениями равна 15,006 . Чтобы определить, является ли это статистически значимым результатом, нам нужно сравнить его с критическим значением F, найденным в таблице распределения F со следующими значениями:
- α (уровень значимости) = 0,05
- DF1 (степени свободы числителя) = df между = 2
- DF2 (степени свободы знаменателя) = ошибка df = 8
Мы находим, что критическое значение F составляет 4,459 .
Поскольку статистика F-теста в таблице ANOVA больше критического значения F в таблице распределения F, мы отклоняем нулевую гипотезу. Это означает, что у нас есть достаточно доказательств, чтобы сказать, что существует статистически значимая разница между средним временем ответа лекарств.