Как рассчитать dfbetas в r

В статистике мы часто хотим знать, какое влияние оказывают различные наблюдения на регрессионные модели.

Один из способов расчета влияния наблюдений — использовать метрику, известную как DFBETAS , которая сообщает нам стандартизированный эффект на каждый коэффициент удаления каждого отдельного наблюдения.

Эта метрика дает нам представление о влиянии каждого наблюдения на оценку каждого коэффициента в данной регрессионной модели.

В этом руководстве показан пошаговый пример того, как рассчитать и визуализировать DFBETAS для каждого наблюдения в модели в R.

Шаг 1. Создайте регрессионную модель

Сначала мы создадим модель множественной линейной регрессии, используя набор данных mtcars , встроенный в R:

 #fit a regression model
model <- lm(mpg~disp+hp, data=mtcars)

#view model summary
summary(model)

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) 30.735904 1.331566 23.083 < 2nd-16 ***
available -0.030346 0.007405 -4.098 0.000306 ***
hp -0.024840 0.013385 -1.856 0.073679 .  
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 3.127 on 29 degrees of freedom
Multiple R-squared: 0.7482, Adjusted R-squared: 0.7309 
F-statistic: 43.09 on 2 and 29 DF, p-value: 2.062e-09

Шаг 2. Рассчитайте DFBETAS для каждого наблюдения.

Далее мы воспользуемся встроенной функцией dfbetas() для расчета значений DFBETAS для каждого наблюдения в модели:

 #calculate DFBETAS for each observation in the model
dfbetas <- as . data . frame (dfbetas(model))

#display DFBETAS for each observation
dfbetas

                      (Intercept) disp hp
Mazda RX4 -0.1174171253 0.030760632 1.748143e-02
Mazda RX4 Wag -0.1174171253 0.030760632 1.748143e-02
Datsun 710 -0.1694989349 0.086630144 -3.332781e-05
Hornet 4 Drive 0.0577309674 0.078971334 -8.705488e-02
Hornet Sportabout -0.0204333878 0.237526523 -1.366155e-01
Valiant -0.1711908285 -0.139135639 1.829038e-01
Duster 360 -0.0312338677 -0.005356209 3.581378e-02
Merc 240D -0.0312259577 -0.010409922 2.433256e-02
Merc 230 -0.0865872595 0.016428917 2.287867e-02
Merc 280 -0.1560683502 0.078667906 -1.911180e-02
Merc 280C -0.2254489597 0.113639937 -2.760800e-02
Merc 450SE 0.0022844093 0.002966155 -2.855985e-02
Merc 450SL 0.0009062022 0.001176644 -1.132941e-02
Merc 450SLC 0.0041566755 0.005397169 -5.196706e-02
Cadillac Fleetwood 0.0388832216 -0.134511133 7.277283e-02
Lincoln Continental 0.0483781688 -0.121146607 5.326220e-02
Chrysler Imperial -0.1645266331 0.236634429 -3.917771e-02
Fiat 128 0.5720358325 -0.181104179 -1.265475e-01
Honda Civic 0.3490872162 -0.053660545 -1.326422e-01
Toyota Corolla 0.7367058819 -0.268512348 -1.342384e-01
Toyota Corona -0.2181110386 0.101336902 5.945352e-03
Dodge Challenger -0.0270169005 -0.123610713 9.441241e-02
AMC Javelin -0.0406785103 -0.141711468 1.074514e-01
Camaro Z28 0.0390139262 0.012846225 -5.031588e-02
Pontiac Firebird -0.0549059340 0.574544346 -3.689584e-01
Fiat X1-9 0.0565157245 -0.017751582 -1.262221e-02
Porsche 914-2 0.0839169111 -0.028670987 -1.240452e-02
Lotus Europa 0.3444562478 -0.402678927 2.135224e-01
Ford Pantera L -0.1598854695 -0.094184733 2.320845e-01
Ferrari Dino -0.0343997122 0.248642444 -2.344154e-01
Maserati Bora -0.3436265545 -0.511285637 7.319066e-01
Volvo 142E -0.1784974091 0.132692956 -4.433915e-02

Для каждого наблюдения мы можем видеть разницу в оценке коэффициентов для начала координат, переменной disp и переменной hp , которая возникает, когда мы удаляем это конкретное наблюдение.

Обычно мы считаем, что наблюдение оказывает сильное влияние на оценку данного коэффициента, если оно имеет значение DBETAS, превышающее порог 2/√ n , где n — количество наблюдений.

В этом примере порог будет 0,3535534 :

 #find number of observations
n <- nrow (mtcars)

#calculate DFBETAS threshold value
thresh <- 2/ sqrt (n)

thresh

[1] 0.3535534

Шаг 3. Визуализируйте DFBETAS

Наконец, мы можем создать графики для визуализации значения DFBETAS для каждого наблюдения и для каждого предиктора в модели:

 #specify 2 rows and 1 column in plotting region
by(mfrow=c(2,1))

#plot DFBETAS for disp with threshold lines
plot(dfbetas$disp, type=' h ')
abline(h = thresh, lty = 2)
abline(h = -thresh, lty = 2)

#plot DFBETAS for hp with threshold lines 
plot(dfbetas$hp, type=' h ')
abline(h = thresh, lty = 2)
abline(h = -thresh, lty = 2)

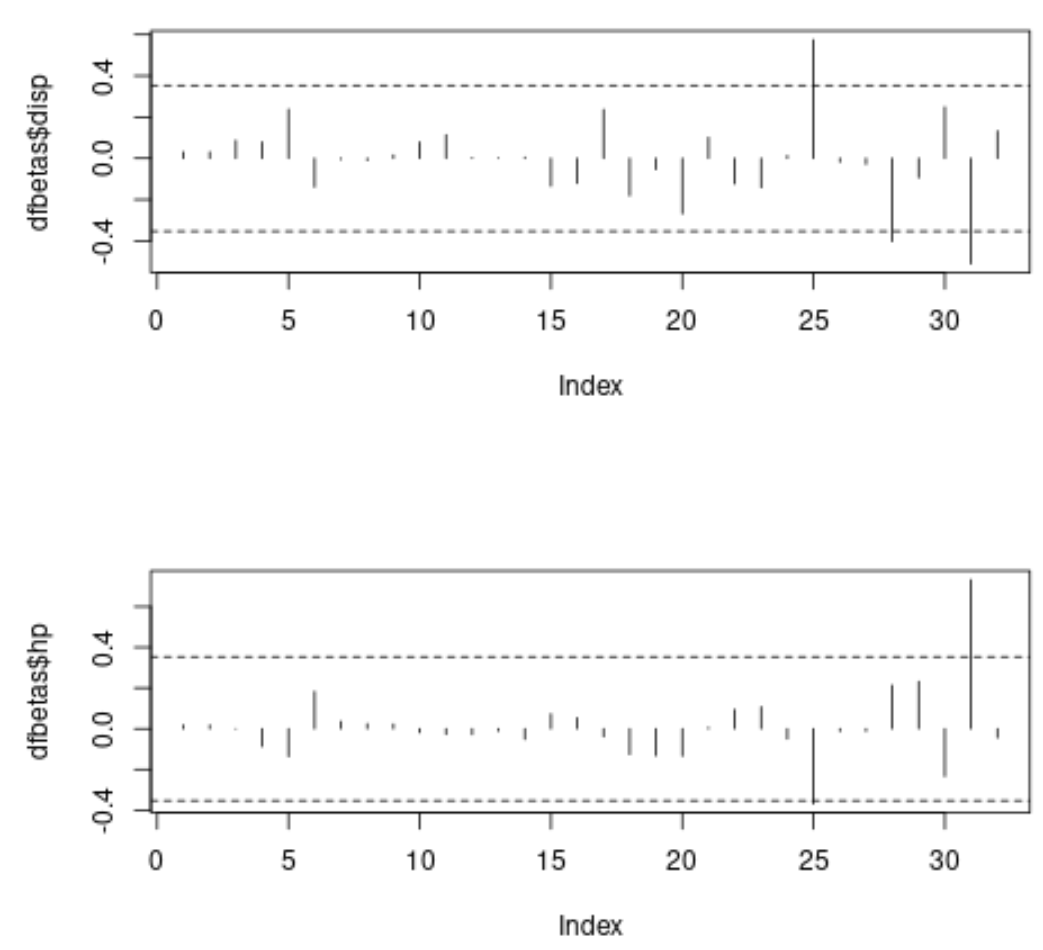
На каждом графике ось X отображает индекс каждого наблюдения в наборе данных, а значение Y отображает соответствующий DFBETAS для каждого наблюдения и каждого предиктора.

На первом графике мы видим, что три наблюдения превышают абсолютное пороговое значение 0,3535534 , а на втором графике мы видим, что два наблюдения превышают абсолютное пороговое значение.

Мы можем решить изучить эти наблюдения более внимательно, чтобы определить, оказывают ли они чрезмерное влияние на оценку коэффициентов модели.

Дополнительные ресурсы

Как выполнить простую линейную регрессию в R
Как выполнить множественную линейную регрессию в R
Как рассчитать статистику кредитного плеча в R
Как рассчитать DFFITS в R