Как выполнить линейную регрессию в google sheets

Линейная регрессия — это метод, который можно использовать для количественной оценки взаимосвязи между одной или несколькими объясняющими переменными и переменной отклика .

Мы используем простую линейную регрессию, когда имеется только одна объясняющая переменная, и множественную линейную регрессию, когда имеется две или более объясняющих переменных.

Оба типа регрессий можно выполнить с помощью функции ЛИНЕЙН() в Google Таблицах, которая использует следующий синтаксис:

ЛИНЕЙН (известные_данные_y, известные_данные_x, вычисление_b, подробный)

Золото:

• известные_данные_y: массив значений ответа
• известные_данные_x: Таблица пояснительных значений.
• вычисление_b: указывает, следует ли вычислять перехват. По умолчанию это TRUE, и мы оставляем это для линейной регрессии.
• Подробный: указывает, следует ли предоставлять дополнительную статистику регрессии, помимо наклона и точки пересечения. По умолчанию это ЛОЖЬ, но в наших примерах мы укажем, что это ИСТИНА.

Следующие примеры показывают, как использовать эту функцию на практике.

Простая линейная регрессия в Google Таблицах

Предположим, мы хотим понять связь между учебными часами и результатами экзаменов. подготовка к экзамену и полученная на экзамене оценка.

Чтобы изучить эту взаимосвязь, мы можем выполнить простую линейную регрессию, используя часы обучения в качестве объясняющей переменной и результаты экзаменов в качестве переменной ответа.

На следующем снимке экрана показано, как выполнить простую линейную регрессию с использованием набора данных из 20 студентов со следующей формулой, используемой в ячейке D2:

= ЛИНИИ ( B2:B21 , A2:A21 , ИСТИНА , ИСТИНА )

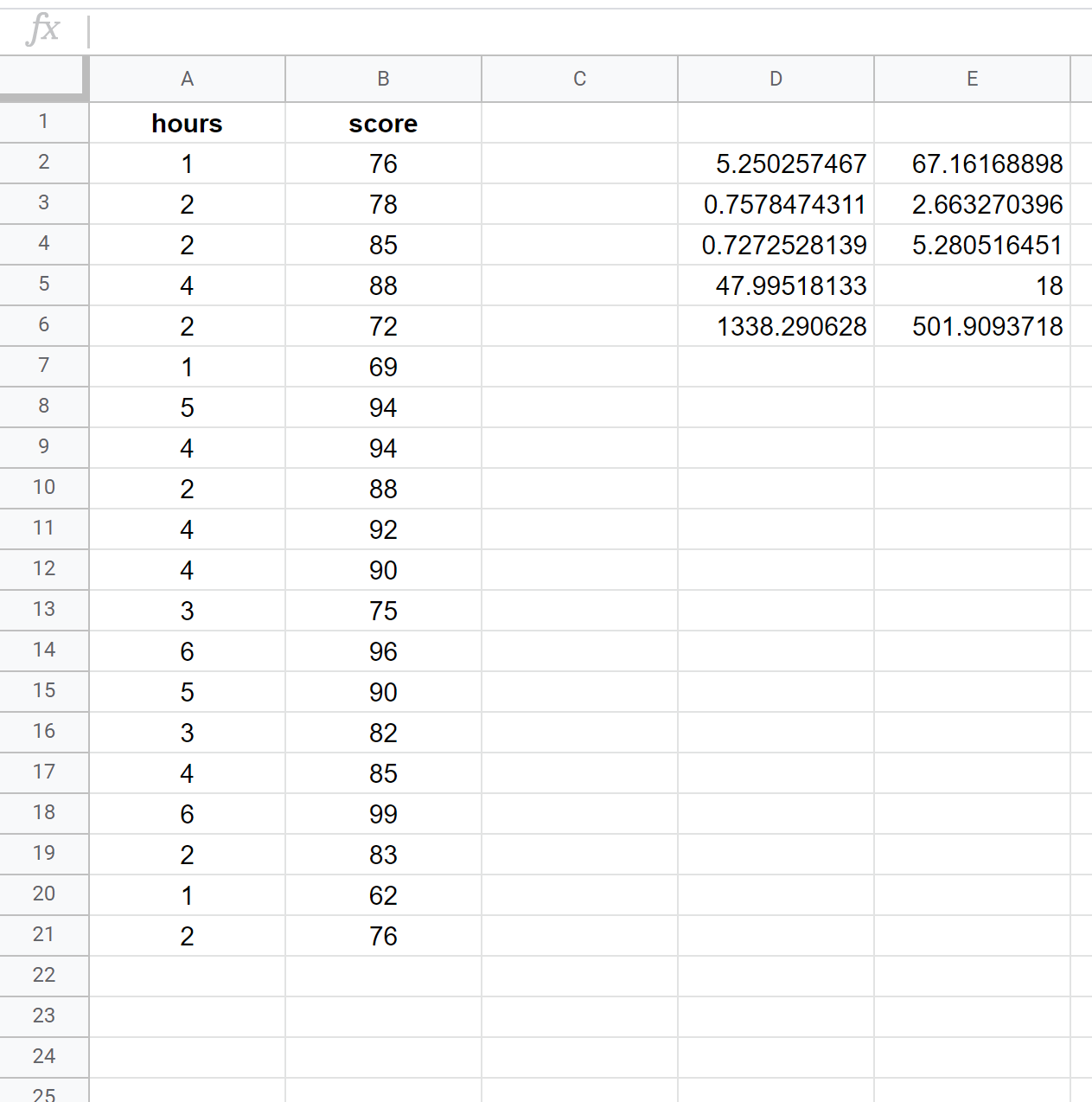
На следующем снимке экрана представлены аннотации к выводу:

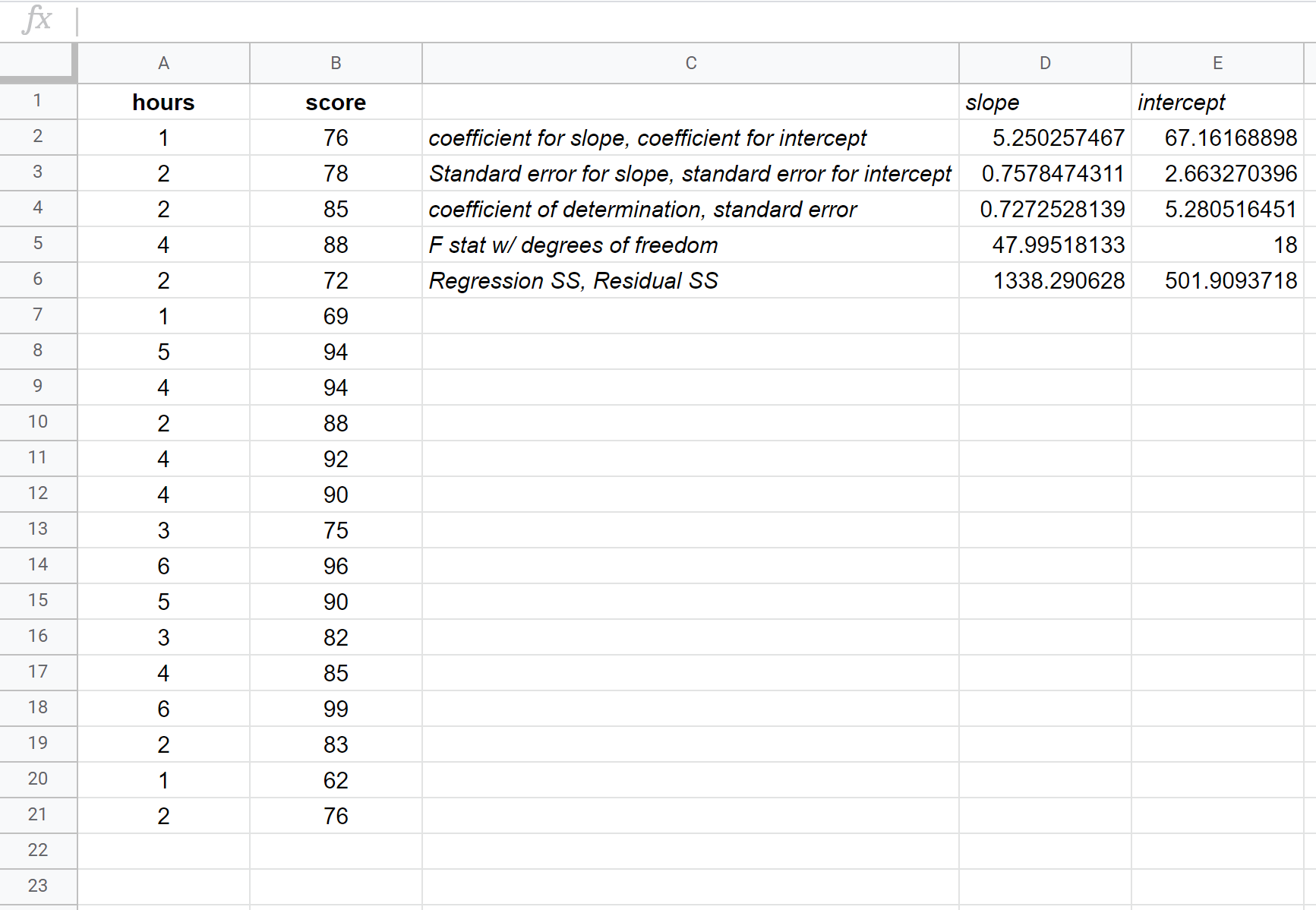
Вот как интерпретировать наиболее релевантные числа в результате:

R Квадрат: 0,72725 . Это называется коэффициентом детерминации. Это доля дисперсии переменной отклика, которую можно объяснить объясняющей переменной. В этом примере примерно 72,73% разницы в результатах экзамена можно объяснить количеством изученных часов.

Стандартная ошибка: 5.2805 . Это среднее расстояние между наблюдаемыми значениями и линией регрессии. В данном примере наблюдаемые значения отклоняются в среднем на 5,2805 единиц от линии регрессии.

Коэффициенты. Коэффициенты дают нам числа, необходимые для написания расчетного уравнения регрессии. В этом примере предполагаемое уравнение регрессии:

Оценка за экзамен = 67,16 + 5,2503*(часы)

Мы интерпретируем коэффициент часов так, что за каждый дополнительный учебный час экзаменационный балл должен увеличиться в среднем на 5,2503 . Мы интерпретируем коэффициент пересечения как означающий, что ожидаемый результат экзамена для студента, обучающегося ноль часов, составляет 67,16 .

Мы можем использовать это предполагаемое уравнение регрессии для расчета ожидаемого результата экзамена для студента на основе количества учебных часов. Например, студент, который учится три часа, должен набрать на экзамене балл 82,91 :

Оценка экзамена = 67,16 + 5,2503*(3) = 82,91

Множественная линейная регрессия в Google Таблицах

Предположим, мы хотим знать, влияет ли количество часов, потраченных на обучение, и количество сданных подготовительных экзаменов на оценку, которую студент получает на определенном вступительном экзамене в колледж.

Чтобы изучить эту взаимосвязь, мы можем выполнить множественную линейную регрессию, используя часы обучения и подготовительные экзамены в качестве объясняющих переменных, а результаты экзаменов — в качестве переменной ответа.

На следующем снимке экрана показано, как выполнить множественную линейную регрессию с использованием набора данных из 20 студентов со следующей формулой, используемой в ячейке E2:

= ПРАВО ( C2:C21 , A2:B21 , ИСТИНА , ИСТИНА )

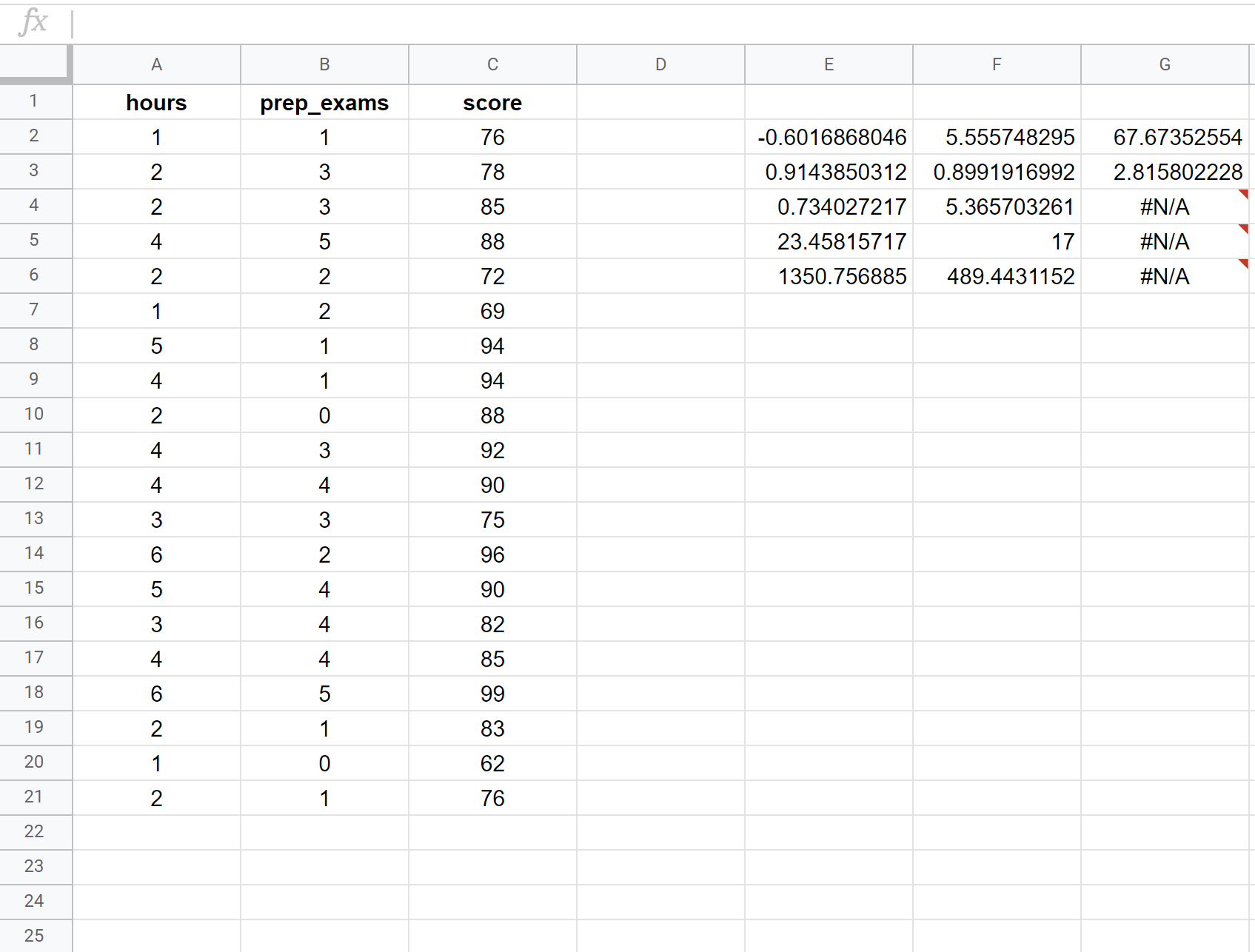
Вот как интерпретировать наиболее релевантные числа в результате:

R Квадрат: 0,734 . Это называется коэффициентом детерминации. Это доля дисперсии переменной отклика, которую можно объяснить объясняющими переменными. В этом примере 73,4% разницы в экзаменационных баллах объясняется количеством учебных часов и количеством сданных подготовительных экзаменов.

Стандартная ошибка: 5.3657 . Это среднее расстояние между наблюдаемыми значениями и линией регрессии. В данном примере наблюдаемые значения отклоняются в среднем на 5,3657 единиц от линии регрессии.

Расчетное уравнение регрессии: мы можем использовать коэффициенты из выходных данных модели, чтобы создать следующее расчетное уравнение регрессии:

Экзаменационный балл = 67,67 + 5,56*(часы) – 0,60*(подготовительные экзамены)

Мы можем использовать это предполагаемое уравнение регрессии для расчета ожидаемого результата экзамена для студента на основе количества часов обучения и количества практических экзаменов, которые он сдает. Например, студент, который учится три часа и сдает подготовительный экзамен, должен получить оценку 83,75 :

Оценка на экзамене = 67,67 + 5,56*(3) – 0,60*(1) = 83,75

Дополнительные ресурсы

В следующих руководствах объясняется, как выполнять другие распространенные задачи в Google Таблицах:

Как выполнить полиномиальную регрессию в Google Sheets
Как создать остаточный график в Google Sheets