Кластеризация k-средних в r: пошаговый пример
Кластеризация — это метод машинного обучения, который пытается найти группы наблюдений в наборе данных.
Цель состоит в том, чтобы найти кластеры, в которых наблюдения внутри каждого кластера очень похожи друг на друга, а наблюдения в разных кластерах сильно отличаются друг от друга.
Кластеризация — это форма обучения без учителя , поскольку мы просто пытаемся найти структуру в наборе данных, а не предсказать значение переменной ответа .
Кластеризация часто используется в маркетинге, когда предприятия имеют доступ к такой информации, как:
- Семейный доход
- Размер семьи
- Глава семьи Профессия
- Расстояние до ближайшего населенного пункта
Когда эта информация доступна, кластеризацию можно использовать для выявления схожих домохозяйств, которые с большей вероятностью будут покупать определенные продукты или лучше реагировать на определенный тип рекламы.
Одна из наиболее распространенных форм кластеризации известна как кластеризация k-средних .
Что такое кластеризация K-средних?
Кластеризация K-средних — это метод, при котором мы помещаем каждое наблюдение из набора данных в один из K- кластеров.
Конечная цель состоит в том, чтобы иметь K кластеров, в которых наблюдения внутри каждого кластера очень похожи друг на друга, в то время как наблюдения в разных кластерах сильно отличаются друг от друга.
На практике мы используем следующие шаги для выполнения кластеризации K-средних:
1. Выберите значение К.
- Во-первых, нам нужно решить, сколько кластеров мы хотим идентифицировать в данных. Часто нам просто нужно протестировать несколько разных значений K и проанализировать результаты, чтобы увидеть, какое количество кластеров кажется наиболее подходящим для конкретной задачи.
2. Случайным образом отнесите каждое наблюдение к начальному кластеру от 1 до K.
3. Выполняйте следующую процедуру, пока назначения кластера не перестанут меняться.
- Для каждого из K кластеров вычислите центр тяжести кластера. Это просто вектор p- средних особенностей для наблюдений k-го кластера.
- Назначьте каждое наблюдение кластеру с ближайшим центроидом. Здесь ближайший определяется с использованием евклидова расстояния .
Кластеризация K-средних в R
В следующем руководстве представлен пошаговый пример выполнения кластеризации k-средних в R.
Шаг 1. Загрузите необходимые пакеты
Сначала мы загрузим два пакета, содержащие несколько полезных функций для кластеризации k-средних в R.
library (factoextra) library (cluster)
Шаг 2. Загрузите и подготовьте данные
В этом примере мы будем использовать набор данных USArrests , встроенный в R, который содержит количество арестов на 100 000 человек в каждом штате США в 1973 году за убийства , нападения и изнасилования , а также процент населения каждого штата, проживающего в городах. области. , Урбанпоп .
Следующий код показывает, как сделать следующее:
- Загрузить набор данных USArrests
- Удалить все строки с пропущенными значениями
- Масштабируйте каждую переменную в наборе данных так, чтобы ее среднее значение было равно 0, а стандартное отклонение — 1.
#load data df <-USArrests #remove rows with missing values df <- na. omitted (df) #scale each variable to have a mean of 0 and sd of 1 df <- scale(df) #view first six rows of dataset head(df) Murder Assault UrbanPop Rape Alabama 1.24256408 0.7828393 -0.5209066 -0.003416473 Alaska 0.50786248 1.1068225 -1.2117642 2.484202941 Arizona 0.07163341 1.4788032 0.9989801 1.042878388 Arkansas 0.23234938 0.2308680 -1.0735927 -0.184916602 California 0.27826823 1.2628144 1.7589234 2.067820292 Colorado 0.02571456 0.3988593 0.8608085 1.864967207
Шаг 3. Найдите оптимальное количество кластеров
Чтобы выполнить кластеризацию k-средних в R, мы можем использовать встроенную функцию kmeans() , которая использует следующий синтаксис:
kmeans (данные, центры, nstart)
Золото:
- данные: Имя набора данных.
- центры: количество кластеров, обозначенное k .
- nstart: количество начальных конфигураций. Поскольку возможно, что разные начальные стартовые кластеры приведут к разным результатам, рекомендуется использовать несколько разных начальных конфигураций. Алгоритм k-средних найдет начальные конфигурации, которые приводят к наименьшему отклонению внутри кластера.
Поскольку мы заранее не знаем, какое количество кластеров является оптимальным, мы создадим два разных графика, которые помогут нам принять решение:
1. Количество кластеров относительно общего количества в сумме квадратов
Сначала мы воспользуемся функцией fviz_nbclust() , чтобы построить график зависимости количества кластеров от суммы квадратов:
fviz_nbclust(df, kmeans, method = “ wss ”)
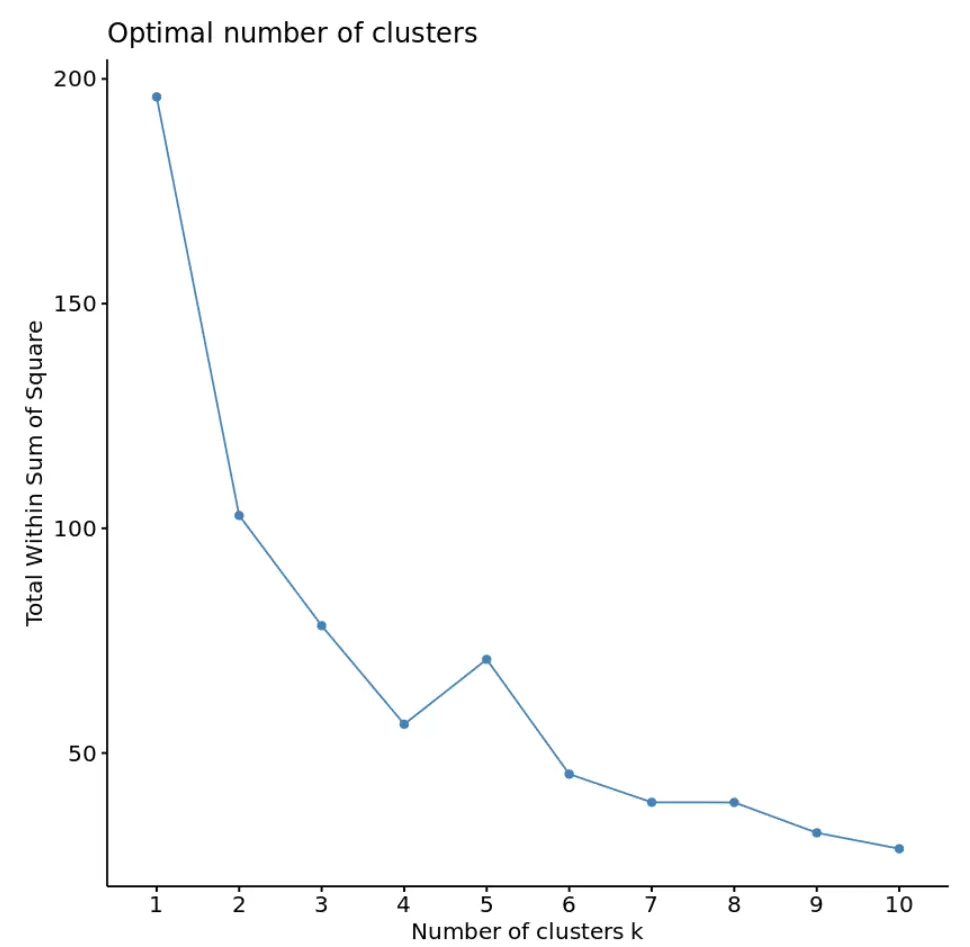
Обычно, когда мы создаем график такого типа, мы ищем «колено», где сумма квадратов начинает «изгибаться» или выравниваться. Обычно это оптимальное количество кластеров.
На этом графике видно, что имеется небольшой излом или «изгиб» при k = 4 кластерах.
2. Количество кластеров в сравнении со статистикой пробелов
Другой способ определить оптимальное количество кластеров — использовать метрику, называемую статистикой отклонений , которая сравнивает общую внутрикластерную вариацию для разных значений k с их ожидаемыми значениями для распределения без кластеризации.
Мы можем вычислить статистику разрыва для каждого количества кластеров, используя функцию clusGap() из пакета кластеров , а также построить график кластеров по статистике разрывов, используя функцию fviz_gap_stat() :
#calculate gap statistic based on number of clusters gap_stat <- clusGap(df, FUN = kmeans, nstart = 25, K.max = 10, B = 50) #plot number of clusters vs. gap statistic fviz_gap_stat(gap_stat)
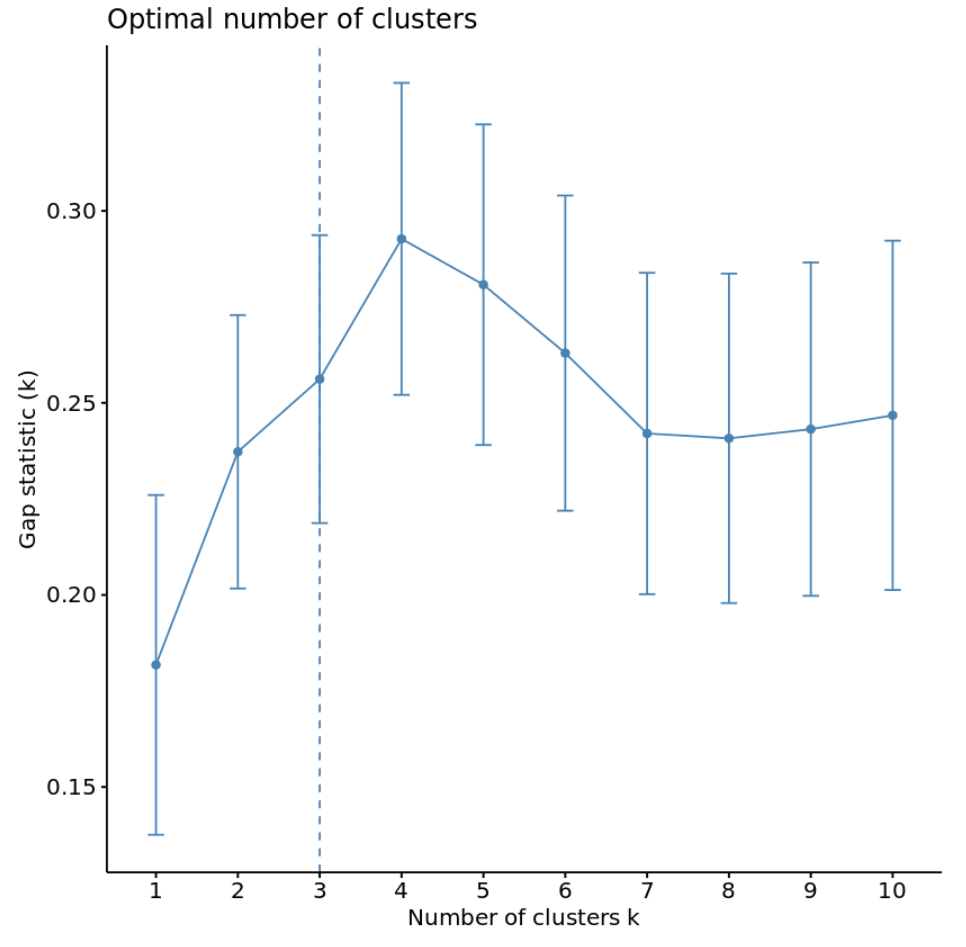
На графике мы видим, что статистика разрывов самая высокая при k = 4 кластерах, что соответствует методу локтя, который мы использовали ранее.
Шаг 4. Выполните кластеризацию K-средних с оптимальным K
Наконец, мы можем выполнить кластеризацию по k-средним в наборе данных, используя оптимальное значение для k , равное 4:
#make this example reproducible set.seed(1) #perform k-means clustering with k = 4 clusters km <- kmeans(df, centers = 4, nstart = 25) #view results km K-means clustering with 4 clusters of sizes 16, 13, 13, 8 Cluster means: Murder Assault UrbanPop Rape 1 -0.4894375 -0.3826001 0.5758298 -0.26165379 2 -0.9615407 -1.1066010 -0.9301069 -0.96676331 3 0.6950701 1.0394414 0.7226370 1.27693964 4 1.4118898 0.8743346 -0.8145211 0.01927104 Vector clustering: Alabama Alaska Arizona Arkansas California Colorado 4 3 3 4 3 3 Connecticut Delaware Florida Georgia Hawaii Idaho 1 1 3 4 1 2 Illinois Indiana Iowa Kansas Kentucky Louisiana 3 1 2 1 2 4 Maine Maryland Massachusetts Michigan Minnesota Mississippi 2 3 1 3 2 4 Missouri Montana Nebraska Nevada New Hampshire New Jersey 3 2 2 3 2 1 New Mexico New York North Carolina North Dakota Ohio Oklahoma 3 3 4 2 1 1 Oregon Pennsylvania Rhode Island South Carolina South Dakota Tennessee 1 1 1 4 2 4 Texas Utah Vermont Virginia Washington West Virginia 3 1 2 1 1 2 Wisconsin Wyoming 2 1 Within cluster sum of squares by cluster: [1] 16.212213 11.952463 19.922437 8.316061 (between_SS / total_SS = 71.2%) Available components: [1] "cluster" "centers" "totss" "withinss" "tot.withinss" "betweenss" [7] "size" "iter" "ifault"
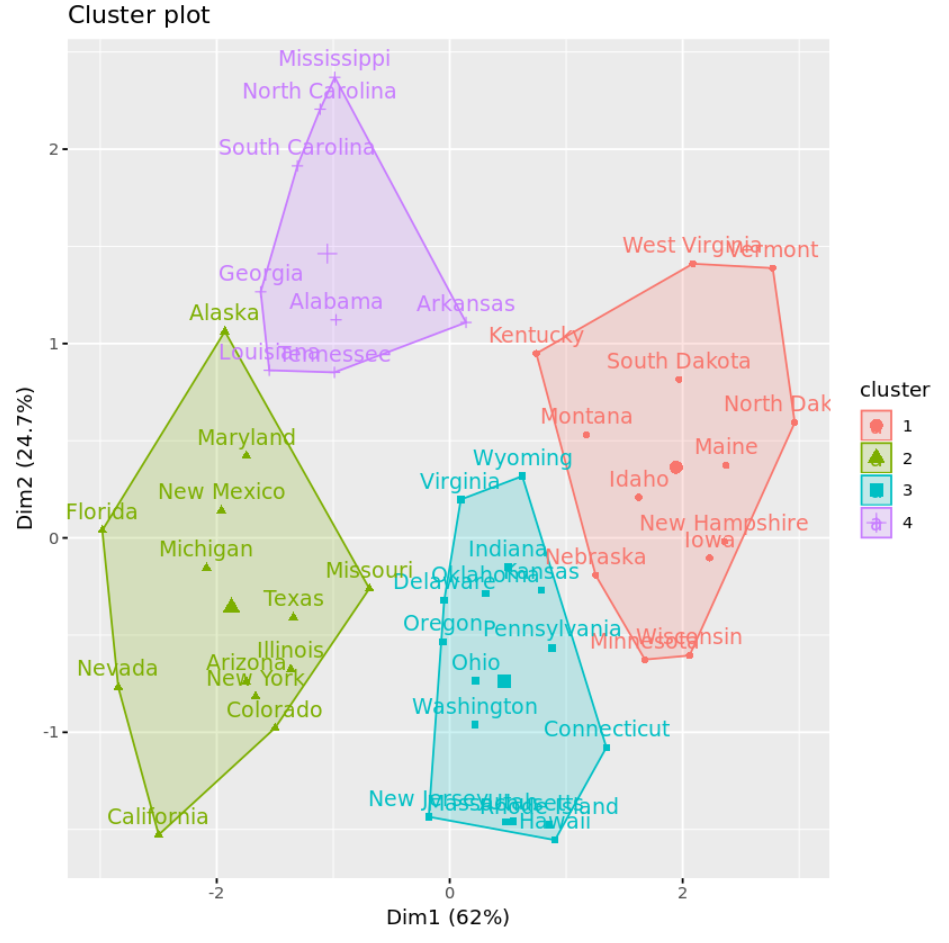
По результатам мы видим, что:
- В первый кластер вошли 16 штатов.
- Во второй кластер вошли 13 штатов.
- В третий кластер отнесены 13 штатов.
- 8 штатов отнесены к четвертому кластеру
Мы можем визуализировать кластеры на диаграмме рассеяния, которая отображает первые два главных компонента на осях, используя функцию fivz_cluster() :
#plot results of final k-means model
fviz_cluster(km, data = df)
Мы также можем использовать функцию Aggregate() , чтобы найти среднее значение переменных в каждом кластере:
#find means of each cluster
aggregate(USArrests, by= list (cluster=km$cluster), mean)
cluster Murder Assault UrbanPop Rape
1 3.60000 78.53846 52.07692 12.17692
2 10.81538 257.38462 76.00000 33.19231
3 5.65625 138.87500 73.87500 18.78125
4 13.93750 243.62500 53.75000 21.41250
Мы интерпретируем этот вывод следующим образом:
- Среднее количество убийств на 100 тысяч граждан среди государств первой группы составляет 3,6 .
- Среднее количество нападений на 100 000 граждан среди государств группы 1 составляет 78,5 .
- Средний процент жителей, проживающих в городской местности среди штатов группы 1, составляет 52,1% .
- Среднее количество изнасилований на 100 000 граждан среди государств группы 1 составляет 12,2 .
И так далее.
Мы также можем добавить назначения кластеров каждого состояния в исходный набор данных:
#add cluster assignment to original data
final_data <- cbind(USArrests, cluster = km$cluster)
#view final data
head(final_data)
Murder Assault UrbanPop Rape cluster
Alabama 13.2 236 58 21.2 4
Alaska 10.0 263 48 44.5 2
Arizona 8.1 294 80 31.0 2
Arkansas 8.8 190 50 19.5 4
California 9.0 276 91 40.6 2
Colorado 7.9 204 78 38.7 2
Преимущества и недостатки кластеризации K-средних
Кластеризация K-средних дает следующие преимущества:
- Это быстрый алгоритм.
- Он может хорошо обрабатывать большие наборы данных.
Однако он имеет следующие потенциальные недостатки:
- Это требует от нас указания количества кластеров перед запуском алгоритма.
- Он чувствителен к выбросам.
Двумя альтернативами кластеризации k-средних являются кластеризация k-средними и иерархическая кластеризация.
Полный код R, использованный в этом примере, вы можете найти здесь .