Кластеризация k-средних в python: пошаговый пример

Один из наиболее распространенных алгоритмов кластеризации в машинном обучении известен как кластеризация k-средних .

Кластеризация K-средних — это метод, при котором мы помещаем каждое наблюдение из набора данных в один из K- кластеров.

Конечная цель состоит в том, чтобы иметь K кластеров, в которых наблюдения внутри каждого кластера очень похожи друг на друга, в то время как наблюдения в разных кластерах сильно отличаются друг от друга.

На практике мы используем следующие шаги для выполнения кластеризации K-средних:

1. Выберите значение К.

• Во-первых, нам нужно решить, сколько кластеров мы хотим идентифицировать в данных. Часто нам просто нужно протестировать несколько разных значений K и проанализировать результаты, чтобы увидеть, какое количество кластеров кажется наиболее подходящим для данной проблемы.

2. Случайным образом отнесите каждое наблюдение к начальному кластеру от 1 до K.

3. Выполняйте следующую процедуру, пока назначения кластера не перестанут меняться.

• Для каждого из K кластеров вычислите центр тяжести кластера. Это просто вектор p- средних особенностей для наблюдений k-го кластера.
• Назначьте каждое наблюдение кластеру с ближайшим центроидом. Здесь ближайший определяется с использованием евклидова расстояния .

В следующем пошаговом примере показано, как выполнить кластеризацию k-средних в Python с помощью функции KMeans из модуля sklearn .

Шаг 1. Импортируйте необходимые модули.

Сначала мы импортируем все модули, которые нам понадобятся для кластеризации k-средних:

 import pandas as pd
import numpy as np
import matplotlib. pyplot as plt
from sklearn. cluster import KMeans
from sklearn. preprocessing import StandardScaler

Шаг 2. Создайте DataFrame

Далее мы создадим DataFrame, содержащий следующие три переменные для 20 разных баскетболистов:

• точки
• помощь
• подпрыгивает

Следующий код показывает, как создать этот DataFrame pandas:

 #createDataFrame
df = pd. DataFrame ({' points ': [18, np.nan, 19, 14, 14, 11, 20, 28, 30, 31,
                              35, 33, 29, 25, 25, 27, 29, 30, 19, 23],
                   ' assists ': [3, 3, 4, 5, 4, 7, 8, 7, 6, 9, 12, 14,
                               np.nan, 9, 4, 3, 4, 12, 15, 11],
                   ' rebounds ': [15, 14, 14, 10, 8, 14, 13, 9, 5, 4,
                                11, 6, 5, 5, 3, 8, 12, 7, 6, 5]})

#view first five rows of DataFrame
print ( df.head ())

   points assists rebounds
0 18.0 3.0 15
1 NaN 3.0 14
2 19.0 4.0 14
3 14.0 5.0 10
4 14.0 4.0 8

Мы будем использовать кластеризацию k-средних, чтобы сгруппировать похожих участников на основе этих трех показателей.

Шаг 3. Очистите и подготовьте DataFrame.

Затем мы выполним следующие шаги:

• Используйте dropna() для удаления строк со значениями NaN в любом столбце
• Используйте StandardScaler() , чтобы масштабировать каждую переменную так, чтобы ее среднее значение было равно 0, а стандартное отклонение равно 1.

Следующий код показывает, как это сделать:

 #drop rows with NA values in any columns
df = df. dropna ()

#create scaled DataFrame where each variable has mean of 0 and standard dev of 1
scaled_df = StandardScaler(). fit_transform (df)

#view first five rows of scaled DataFrame
print (scaled_df[:5])

[[-0.86660275 -1.22683918 1.72722524]
 [-0.72081911 -0.96077767 1.45687694]
 [-1.44973731 -0.69471616 0.37548375]
 [-1.44973731 -0.96077767 -0.16521285]
 [-1.88708823 -0.16259314 1.45687694]]

Примечание . Мы используем масштабирование, чтобы каждая переменная имела одинаковую важность при настройке алгоритма k-средних. В противном случае переменные с самыми широкими диапазонами имели бы слишком большое влияние.

Шаг 4. Найдите оптимальное количество кластеров

Чтобы выполнить кластеризацию k-средних в Python, мы можем использовать функцию KMeans из модуля sklearn .

Эта функция использует следующий базовый синтаксис:

KMeans(init=’random’, n_clusters=8, n_init=10, random_state=None)

Золото:

• init : управляет методом инициализации.
• n_clusters : количество кластеров, в которых можно разместить наблюдения.
• n_init : количество инициализаций, которые необходимо выполнить. По умолчанию алгоритм k-средних запускается 10 раз и возвращается тот, у которого SSE наименьший.
• Случайное_состояние : Целочисленное значение, которое вы можете выбрать, чтобы сделать результаты алгоритма воспроизводимыми.

Самый важный аргумент этой функции — n_clusters, который указывает, в сколько кластеров следует поместить наблюдения.

Однако мы заранее не знаем, какое количество кластеров является оптимальным, поэтому нам нужно создать график, отображающий количество кластеров, а также SSE (сумму квадратов ошибок) модели.

Обычно, когда мы создаем график такого типа, мы ищем «колено», где сумма квадратов начинает «изгибаться» или выравниваться. Обычно это оптимальное количество кластеров.

Следующий код показывает, как создать график этого типа, который отображает количество кластеров по оси X и SSE по оси Y:

 #initialize kmeans parameters
kmeans_kwargs = {
" init ": " random ",
" n_init ": 10,
" random_state ": 1,
}

#create list to hold SSE values for each k
sse = []
for k in range(1, 11):
    kmeans = KMeans(n_clusters=k, ** kmeans_kwargs)
    kmeans. fit (scaled_df)
    sse. append (kmeans.inertia_)

#visualize results
plt. plot (range(1, 11), sse)
plt. xticks (range(1, 11))
plt. xlabel (" Number of Clusters ")
plt. ylabel (“ SSE ”)
plt. show () 

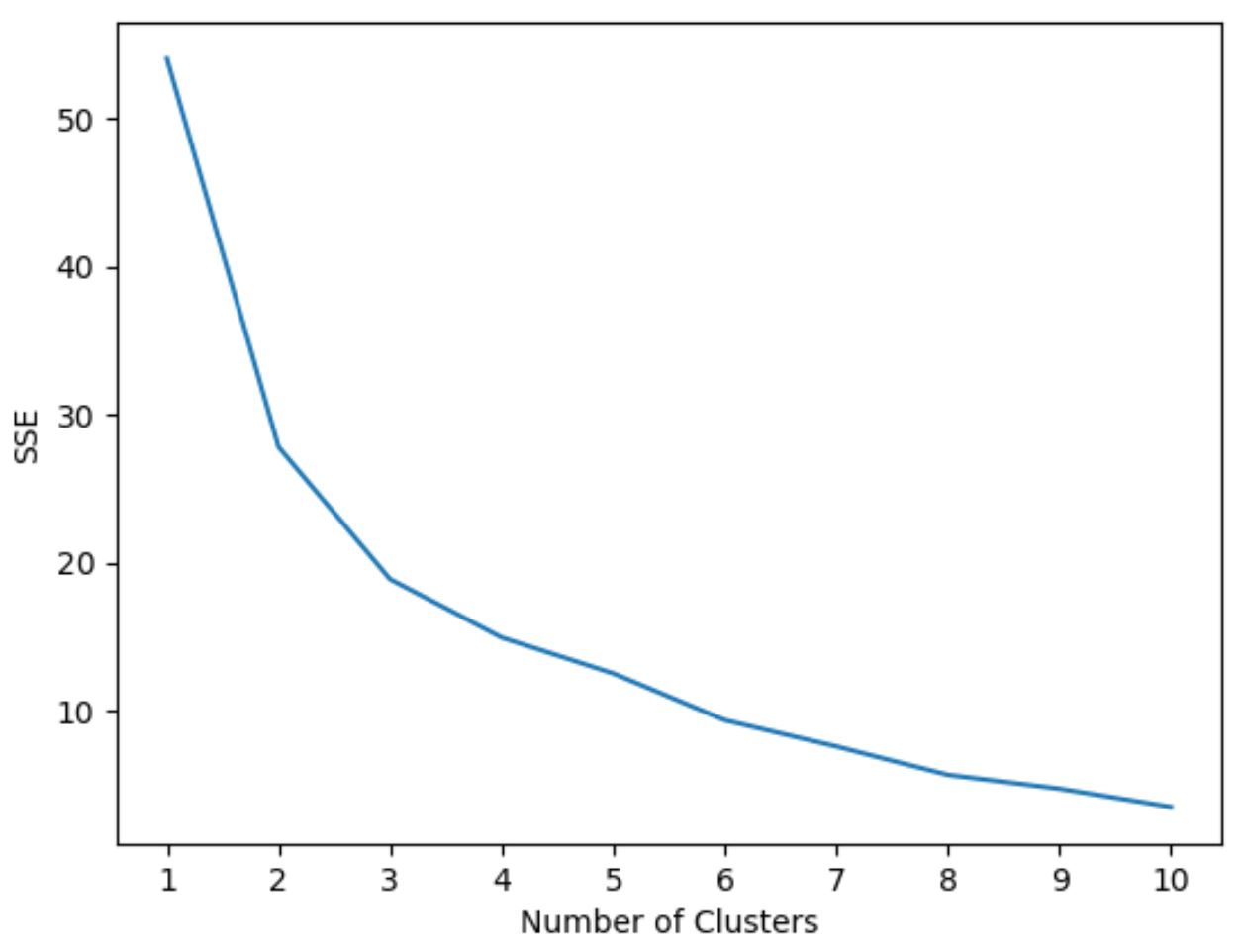
На этом графике видно, что имеется излом или «перелом» при k = 3 кластерах .

Итак, мы будем использовать 3 кластера при настройке нашей модели кластеризации k-средних на следующем этапе.

Примечание . В реальном мире рекомендуется использовать комбинацию этого графика и опыта предметной области, чтобы выбрать количество используемых кластеров.

Шаг 5. Выполните кластеризацию K-средних с оптимальным K

Следующий код показывает, как выполнить кластеризацию по k-средним в наборе данных, используя оптимальное значение для k , равное 3:

 #instantiate the k-means class, using optimal number of clusters
kmeans = KMeans(init=" random ", n_clusters= 3 , n_init= 10 , random_state= 1 )

#fit k-means algorithm to data
kmeans. fit (scaled_df)

#view cluster assignments for each observation
kmeans. labels_

array([1, 1, 1, 1, 1, 1, 2, 2, 0, 0, 0, 0, 2, 2, 2, 0, 0, 0]) 

В результирующей таблице показаны назначения кластеров для каждого наблюдения в DataFrame.

Чтобы облегчить интерпретацию этих результатов, мы можем добавить столбец в DataFrame, который показывает назначение кластера каждому игроку:

 #append cluster assingments to original DataFrame
df[' cluster '] = kmeans. labels_

#view updated DataFrame
print (df)

points assists rebounds cluster
0 18.0 3.0 15 1
2 19.0 4.0 14 1
3 14.0 5.0 10 1
4 14.0 4.0 8 1
5 11.0 7.0 14 1
6 20.0 8.0 13 1
7 28.0 7.0 9 2
8 30.0 6.0 5 2
9 31.0 9.0 4 0
10 35.0 12.0 11 0
11 33.0 14.0 6 0
13 25.0 9.0 5 0
14 25.0 4.0 3 2
15 27.0 3.0 8 2
16 29.0 4.0 12 2
17 30.0 12.0 7 0
18 19.0 15.0 6 0
19 23.0 11.0 5 0

Столбец кластера содержит номер кластера (0, 1 или 2), которому назначен каждый игрок.

Игроки, принадлежащие к одному кластеру, имеют примерно схожие значения столбцов очков , передач и подборов .

Примечание . Полную документацию по функции KMeans sklearn можно найти здесь .

Дополнительные ресурсы

В следующих руководствах объясняется, как выполнять другие распространенные задачи на Python:

Как выполнить линейную регрессию в Python
Как выполнить логистическую регрессию в Python
Как выполнить перекрестную проверку K-Fold в Python