R vs r-square: в чем разница?

Два термина, которые студенты часто путают в статистике, — это R и R-квадрат , часто обозначаемые ^R2 .

В контексте простой линейной регрессии :

• A: Корреляция между переменной-предиктором x и переменной отклика y.
• R ² : Доля дисперсии переменной ответа, которую можно объяснить переменной-предиктором в регрессионной модели.

И в контексте множественной линейной регрессии :

• A: Корреляция между наблюдаемыми значениями переменной ответа и прогнозируемыми значениями переменной ответа, сделанными моделью.
• R ² : Доля дисперсии переменной ответа, которую можно объяснить переменными-предикторами регрессионной модели.

Обратите внимание, что значение R ² находится между 0 и 1. Чем ближе значение к 1, тем сильнее связь между переменной-предиктором и переменной ответа.

В следующих примерах показано, как интерпретировать значения R и R-квадрата в моделях простой линейной регрессии и множественной линейной регрессии.

Пример 1: Простая линейная регрессия

Предположим, у нас есть следующий набор данных, который показывает количество учебных часов и результаты экзаменов, полученные 12 студентами на определенном курсе математики:

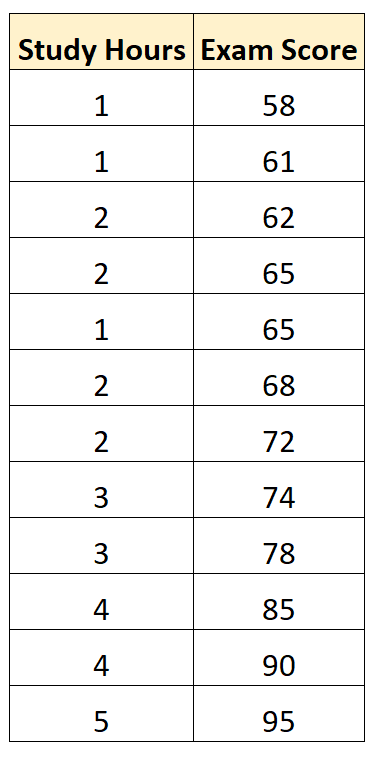
Используя статистическое программное обеспечение (например, Excel, R, Python, SPSS и т. д.), мы можем подогнать простую модель линейной регрессии, используя «учебные часы» в качестве предикторной переменной и «оценку на экзамене» в качестве переменной ответа .

Мы можем найти следующий вывод для этой модели:

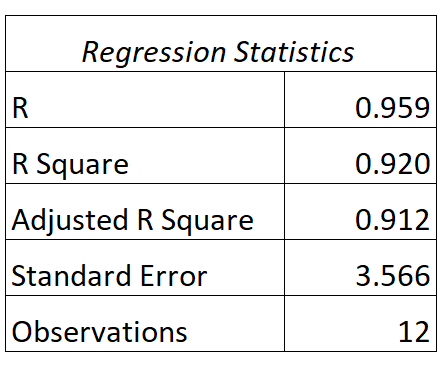
Вот как интерпретировать значения R и R в квадрате этой модели:

• О: Корреляция между учебными часами и баллами на экзамене составляет 0,959 .
• R ² : R в квадрате для этой регрессионной модели составляет 0,920 . Это говорит нам о том, что 92,0% различий в результатах экзаменов можно объяснить количеством изученных часов.

Также обратите внимание, что значение R ² просто равно значению R в квадрате:

^R2 = R * R = 0,959 * 0,959 = 0,920

Пример 2: Множественная линейная регрессия

Предположим, у нас есть следующий набор данных, который показывает количество учебных часов, текущую оценку ученика и оценку на экзамене, полученную 12 студентами по определенному курсу математики:

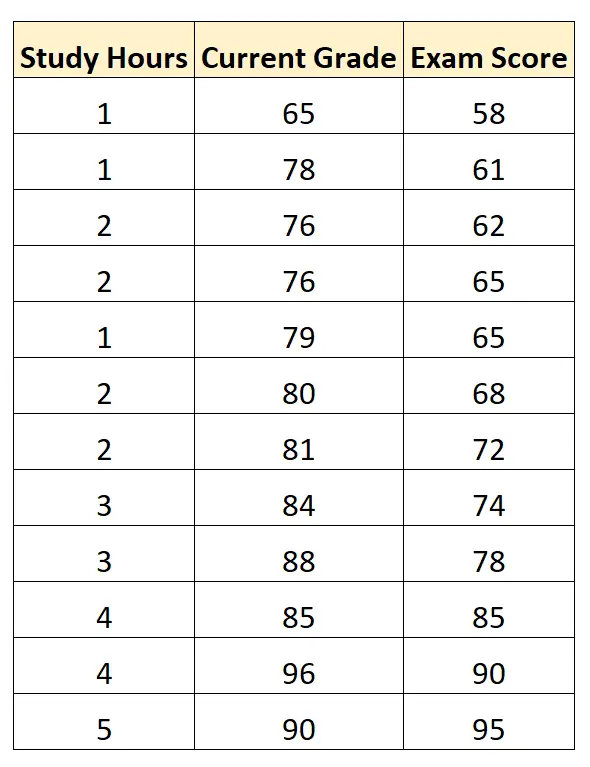
Используя статистическое программное обеспечение, мы можем подогнать модель множественной линейной регрессии, используя «учебные часы» и «текущую оценку» в качестве предикторных переменных и «оценку на экзамене» в качестве переменной ответа.

Мы можем найти следующий вывод для этой модели:

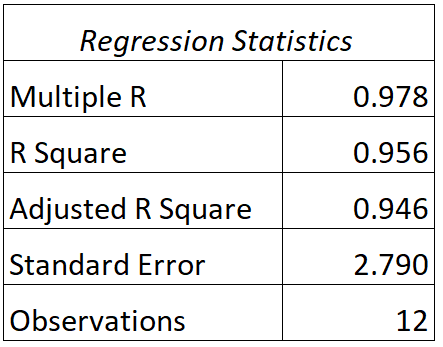
Вот как интерпретировать значения R и R в квадрате этой модели:

• Ответ: Корреляция между фактическими результатами тестов и прогнозируемыми результатами тестов модели составляет 0,978 .
• R ² : R в квадрате для этой регрессионной модели составляет 0,956 . Это говорит нам о том, что 95,6% различий в результатах экзаменов можно объяснить количеством учебных часов и текущей оценкой учащегося в классе.

Также обратите внимание, что значение R ² просто равно значению R в квадрате:

^R2 = R * R = 0,978 * 0,978 = 0,956

Дополнительные ресурсы

Что такое хорошее значение R-квадрата?
Нежный путеводитель по сумме квадратов: SST, SSR, SSE