Rmse против r-квадрата: какую метрику следует использовать?
Модели регрессии используются для количественной оценки взаимосвязи между одной или несколькими переменными-предикторами и переменной отклика.
Всякий раз, когда мы подгоняем регрессионную модель, мы хотим понять, насколько хорошо модель «соответствует» данным. Другими словами, насколько хорошо модель способна использовать значения переменных-предикторов для прогнозирования значения переменной отклика ?
Двумя метриками, которые статистики часто используют для количественной оценки того, насколько хорошо модель соответствует набору данных, являются среднеквадратическая ошибка (RMSE) и R в квадрате ( R2 ), которые рассчитываются следующим образом:
RMSE : метрика, которая сообщает нам, насколько в среднем далеки прогнозируемые значения от наблюдаемых значений в наборе данных. Чем ниже RMSE, тем лучше модель соответствует набору данных.
Он рассчитывается следующим образом:
RMSE = √ Σ(P i – O i ) 2 / n
Золото:
- Σ — символ, означающий «сумма».
- Pi — прогнозируемое значение для i-го наблюдения.
- O i — наблюдаемое значение для i-го наблюдения
- n — размер выборки
R 2 : показатель, который говорит нам, какая часть дисперсии переменной отклика регрессионной модели может быть объяснена переменными-предикторами. Это значение находится в диапазоне от 0 до 1. Чем выше значение R 2 , тем лучше модель соответствует набору данных.
Он рассчитывается следующим образом:
R2 = 1 – (РСС/ТСС)
Золото:
- RSS представляет собой сумму квадратов остатков
- TSS представляет собой общую сумму квадратов
RMSE против R 2 : какую метрику следует использовать?
При оценке соответствия модели набору данных полезно рассчитать как значение RMSE, так и значение R 2 , поскольку каждая метрика говорит нам что-то свое.
С одной стороны, RMSE сообщает нам типичное расстояние между прогнозируемым значением, полученным с помощью регрессионной модели, и истинным значением.
С другой стороны, R 2 говорит нам, в какой степени переменные-предикторы могут объяснить изменение переменной отклика.
Например, предположим, что у нас есть следующий набор данных, который отображает информацию о домах в определенном городе:
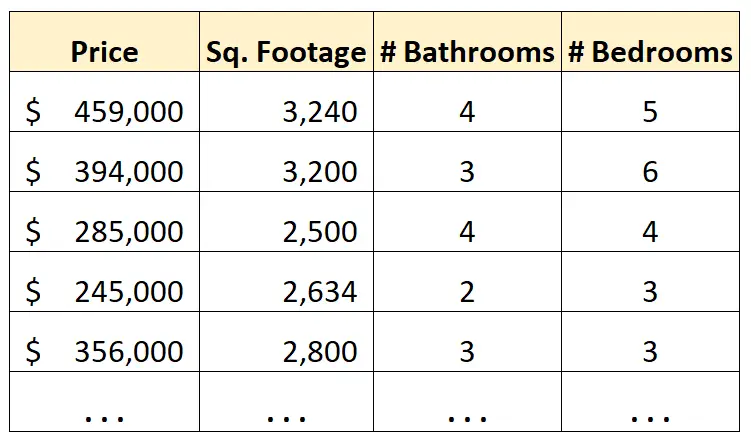
Теперь предположим, что мы хотим использовать квадратные метры, количество ванных комнат и количество спален, чтобы спрогнозировать цену дома.
Мы можем адаптировать следующую регрессионную модель:
Цена = β 0 + β 1 (площадь в квадратных метрах) + β 2 (количество ванных комнат) + β 3 (количество спален)
Теперь предположим, что мы подгоняем эту модель, а затем вычисляем следующие показатели, чтобы оценить степень соответствия модели:
- СКО : 14,342
- Р2 : 0,856
Значение RMSE говорит нам, что средняя разница между прогнозируемой моделью ценой дома и фактической ценой дома составляет 14 342 доллара.
Значение R 2 говорит нам о том, что переменные-предсказатели модели (площадь в квадратных метрах, количество ванных комнат и количество спален) способны объяснить 85,6% изменений цен на жилье.
Чтобы определить, являются ли эти значения «хорошими» или нет, мы можем сравнить эти измерения с альтернативными моделями.
Например, предположим, что мы подбираем другую модель регрессии, которая использует другой набор переменных-предикторов, и вычисляем для этой модели следующие показатели:
- СКО : 19,355
- Р2 : 0,765
Мы видим, что значение RMSE этой модели выше, чем у предыдущей модели. Также видно, что значение R 2 этой модели ниже, чем у предыдущей модели. Это говорит нам о том, что эта модель хуже соответствует данным, чем предыдущая модель.
Краткое содержание
Вот основные моменты, затронутые в этой статье:
- RMSE и R 2 количественно определяют, насколько хорошо регрессионная модель соответствует набору данных.
- RMSE говорит нам, насколько хорошо модель регрессии может предсказать значение переменной ответа в абсолютном выражении, а R 2 говорит нам, насколько хорошо модель может предсказать значение переменной ответа в процентном выражении.
- Полезно рассчитать как RMSE, так и R2 для данной модели, поскольку каждая метрика дает нам полезную информацию.
Дополнительные ресурсы
Введение в множественную линейную регрессию
R vs R-Square: в чем разница?
Что такое хорошее значение R-квадрата?