Как использовать оператор proc glmselect в sas

Вы можете использовать оператор PROC GLMSELECT в SAS, чтобы выбрать лучшую модель регрессии на основе списка потенциальных переменных-предикторов.

Следующий пример показывает, как использовать это утверждение на практике.

Пример. Как использовать PROC GLMSELECT в SAS для выбора модели.

Предположим, мы хотим подобрать модель множественной линейной регрессии, которая использует (1) количество часов, потраченных на учебу, (2) количество сданных подготовительных экзаменов и (3) пол для прогнозирования итоговой оценки учащихся на экзамене.

Сначала мы будем использовать следующий код, чтобы создать набор данных, содержащий эту информацию для 20 студентов:

 /*create dataset*/
data exam_data;
    input hours prep_exams gender $score;
    datalines ;
1 1 0 76
2 3 1 78
2 3 0 85
4 5 0 88
2 2 0 72
1 2 1 69
5 1 1 94
4 1 0 94
2 0 1 88
4 3 0 92
4 4 1 90
3 3 1 75
6 2 1 96
5 4 0 90
3 4 0 82
4 4 1 85
6 5 1 99
2 1 0 83
1 0 1 62
2 1 0 76
;
run ;

/*view dataset*/
proc print data =exam_data;

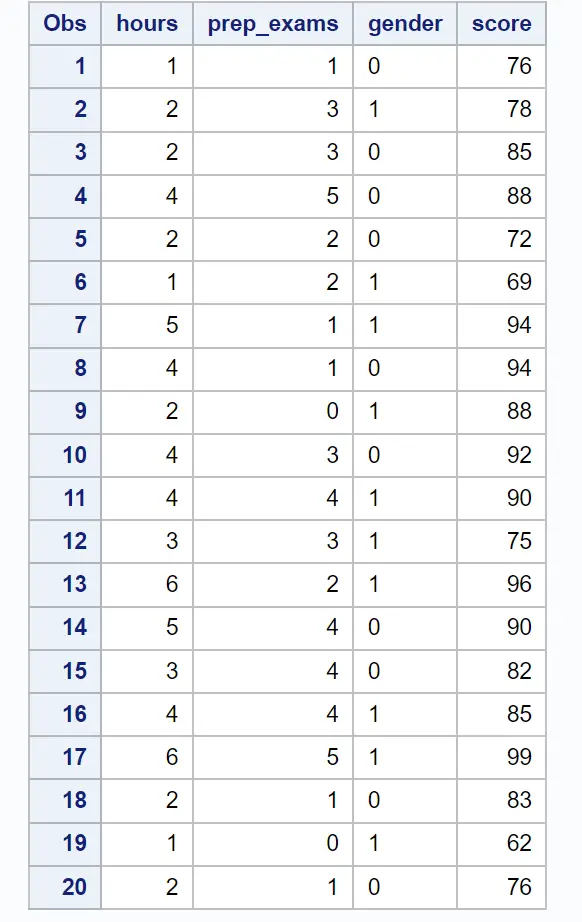
Далее мы будем использовать оператор PROC GLMSELECT , чтобы определить подмножество переменных-предикторов, которое создает лучшую модель регрессии:

 /*perform model selection*/
proc glmselect data =exam_data;
    classgender ;
    model score = hours prep_exams gender;
run ;

Примечание . Мы включили пол в оператор класса , поскольку это категориальная переменная.

Первая группа таблиц в выводе показывает обзор процедуры GLMSELECT:

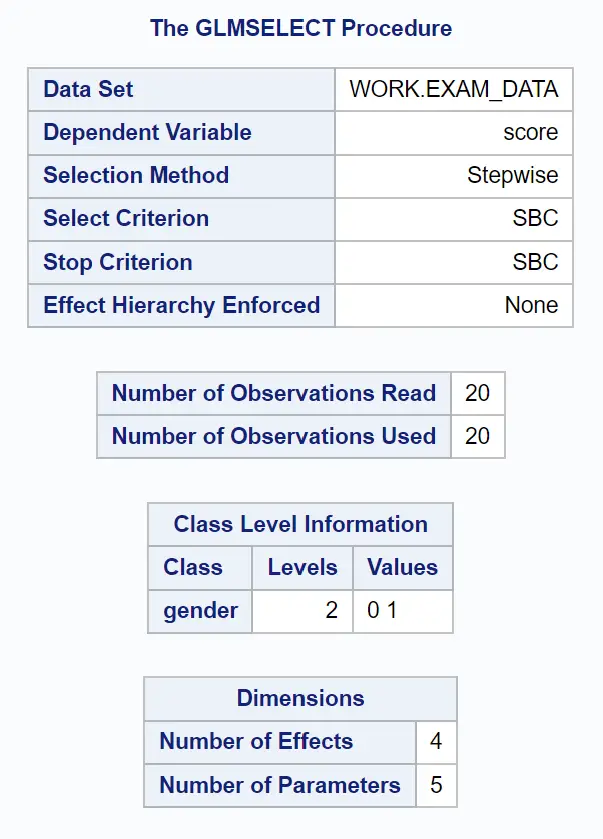
Мы видим, что критерием, используемым для прекращения добавления или удаления переменных из модели, был SBC , который является информационным критерием Шварца , иногда называемым байесовским информационным критерием .

По сути, оператор PROC GLMSELECT продолжает добавлять или удалять переменные из модели до тех пор, пока не найдет модель с наименьшим значением SBC, которая считается «лучшей» моделью.

В следующей группе таблиц показано, чем завершился пошаговый выбор:

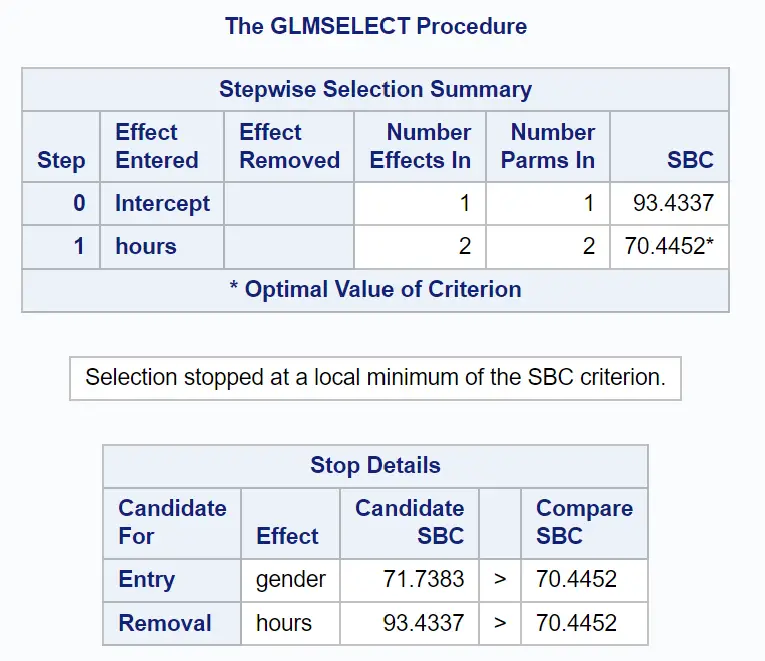
Мы видим, что модель, содержащая только исходный термин, имела значение SBC 93,4337 .

При добавлении часов в качестве предикторной переменной в модель значение SBC упало до 70,4452 .

Лучшим способом улучшить модель было добавить пол в качестве предикторной переменной, но это фактически увеличило значение SBC до 71,7383.

Таким образом, окончательная модель включает в себя только член перехвата и изученные времена.

Последняя часть результата показывает сводку этой подобранной регрессионной модели:

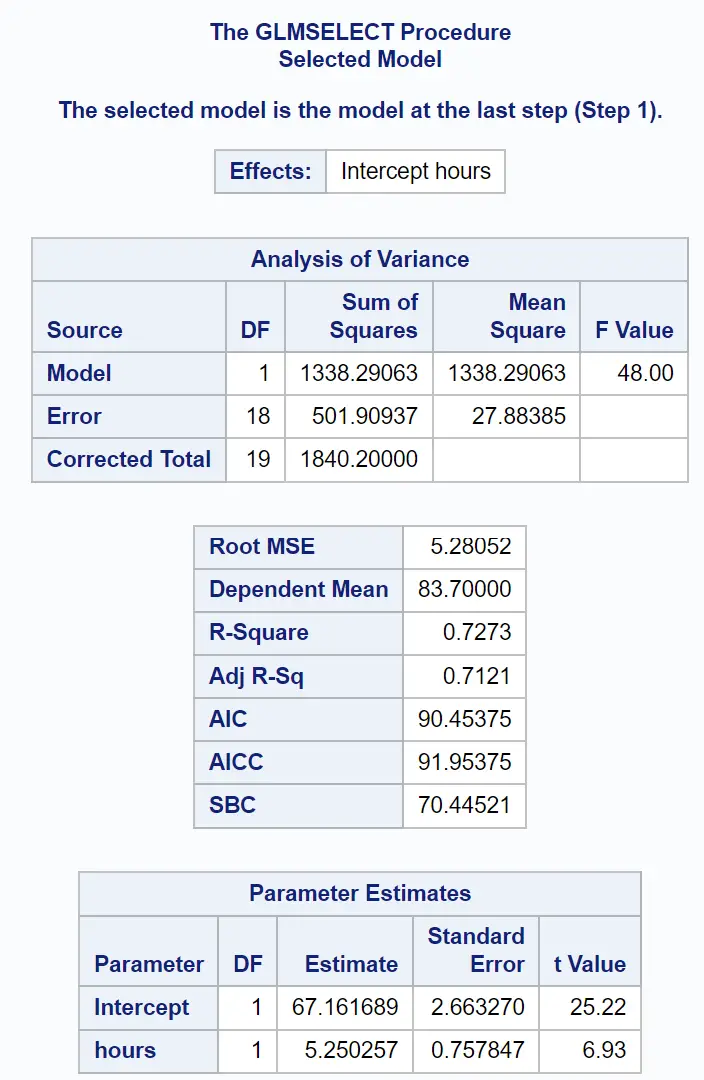
Мы можем использовать значения в таблице «Оценки параметров» для написания подобранной регрессионной модели:

Экзаменационный балл = 67,161689 + 5,250257 (учебные часы)

Мы также можем увидеть различные метрики, которые говорят нам, насколько хорошо эта модель соответствует данным:

Значение R-квадрата показывает нам процент вариации результатов экзаменов, который можно объяснить количеством учебных часов и количеством сданных подготовительных экзаменов.

При этом 72,73% разброса экзаменационных баллов можно объяснить количеством учебных часов и количеством сданных подготовительных экзаменов.

Также полезно знать значение Root MSE . Это представляет собой среднее расстояние между наблюдаемыми значениями и линией регрессии.

В этой регрессионной модели наблюдаемые значения отклоняются в среднем на 5,28052 единицы от линии регрессии.

Примечание . Полный список потенциальных аргументов, которые можно использовать с PROC GLMSELECT, см. в документации SAS .

Дополнительные ресурсы

В следующих руководствах объясняется, как выполнять другие распространенные задачи в SAS:

Как выполнить простую линейную регрессию в SAS
Как выполнить множественную линейную регрессию в SAS
Как выполнить полиномиальную регрессию в SAS
Как выполнить логистическую регрессию в SAS