Как выполнить квадратичную регрессию в spss

Когда две переменные имеют линейную связь, вы часто можете использовать простую линейную регрессию для количественной оценки их связи.

Однако простая линейная регрессия не работает, когда две переменные имеют нелинейную связь. В этих случаях вы можете попробовать использовать квадратичную регрессию .

В этом руководстве объясняется, как выполнить квадратичную регрессию в SPSS.

Пример: квадратичная регрессия в SPSS

Предположим, мы хотим понять взаимосвязь между количеством отработанных часов и счастьем. У нас есть следующие данные о количестве отработанных часов в неделю и уровне счастья (по шкале от 0 до 100) для 16 разных людей:

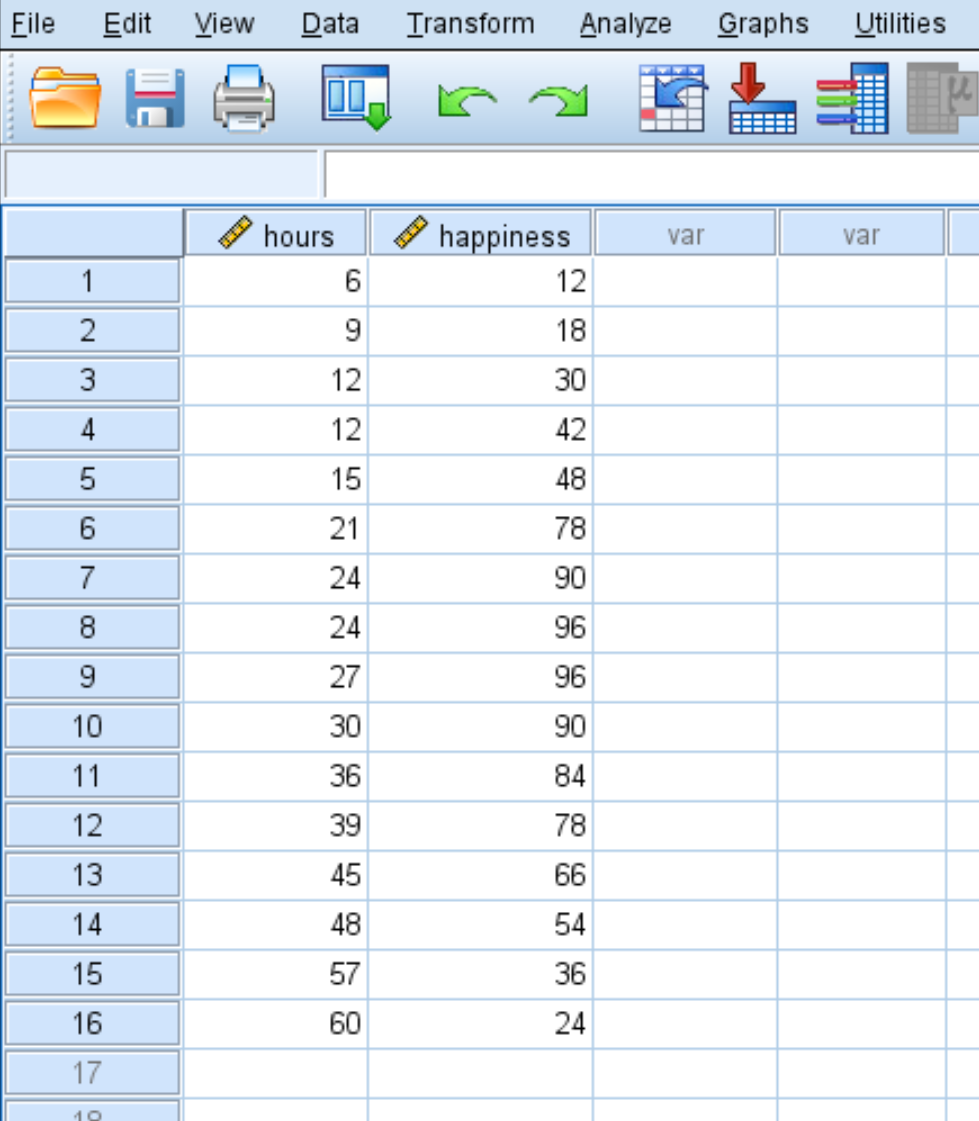
Используйте следующие шаги, чтобы выполнить квадратичную регрессию в SPSS.

Шаг 1: Визуализируйте данные.

Прежде чем выполнять квадратичную регрессию, давайте создадим диаграмму рассеяния, чтобы визуализировать взаимосвязь между отработанными часами и счастьем, чтобы убедиться, что эти две переменные действительно имеют квадратичную связь.

Откройте вкладку «Диаграммы» , затем нажмите «Построитель диаграмм »:

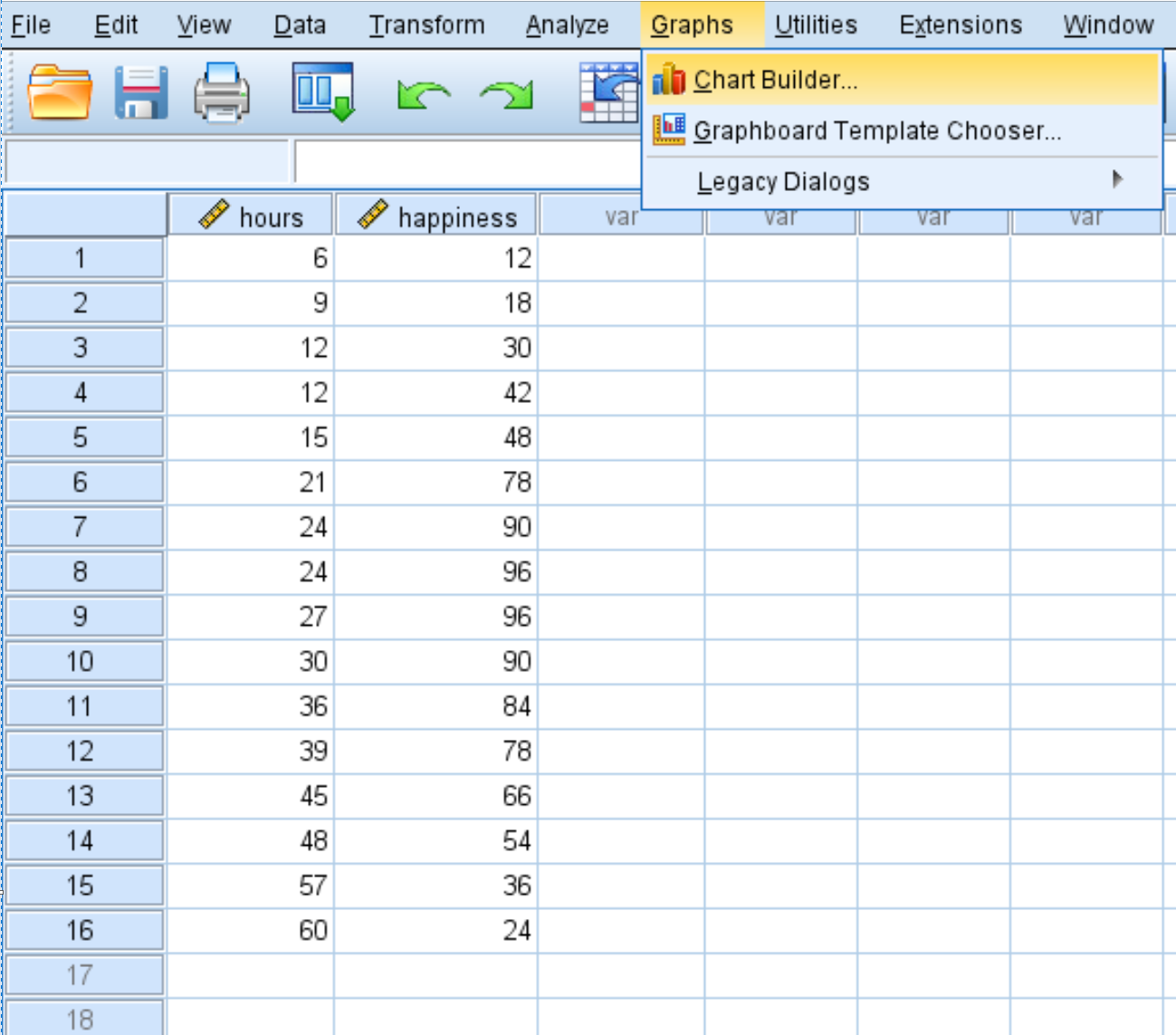
В появившемся новом окне выберите Scatter/Dot из списка Choose from . Затем перетащите диаграмму с надписью Simple Scatter в главное окно редактирования. Перетащите переменные часы по оси X и счастье по оси Y. Затем нажмите ОК .

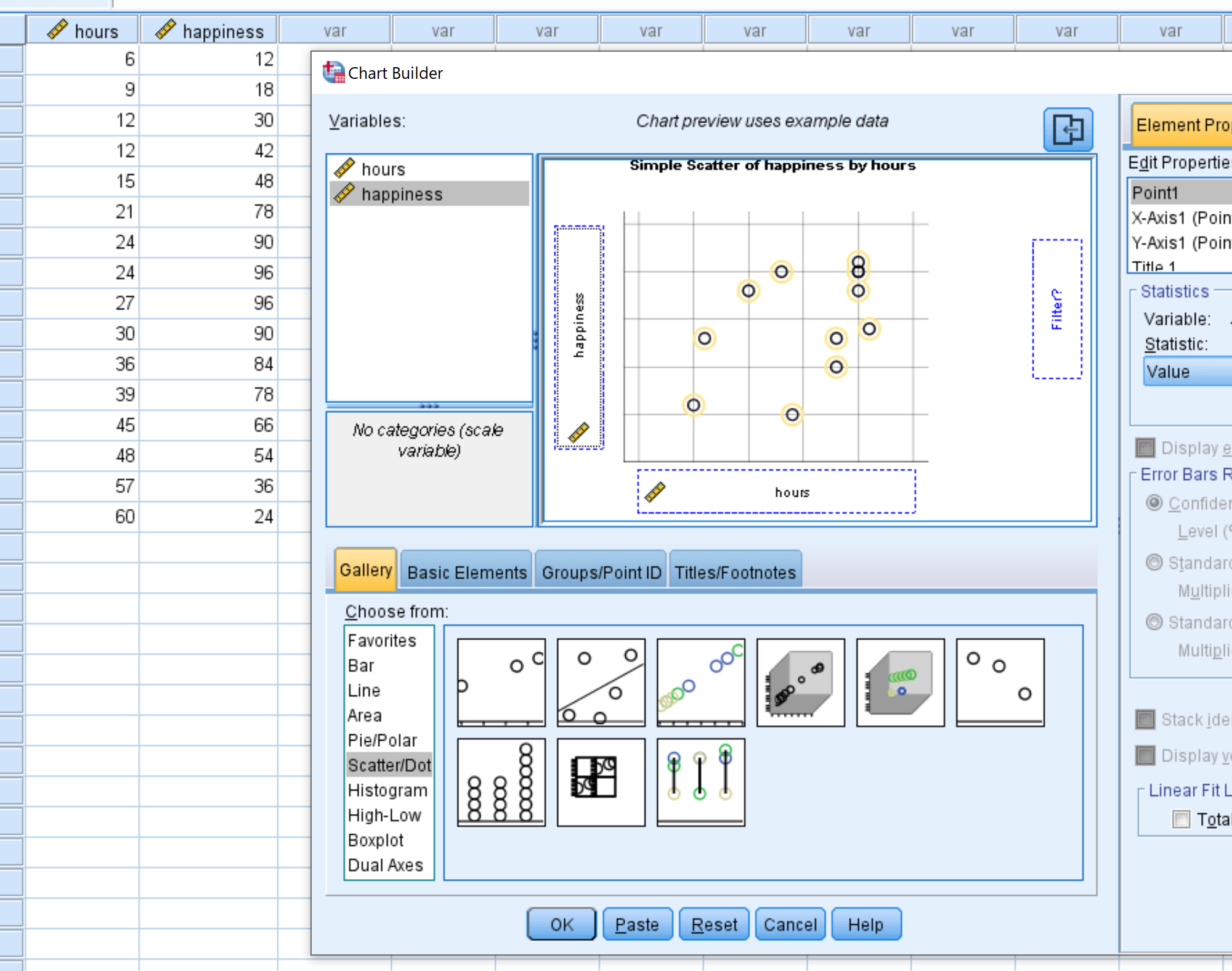
Появится следующая диаграмма рассеяния:

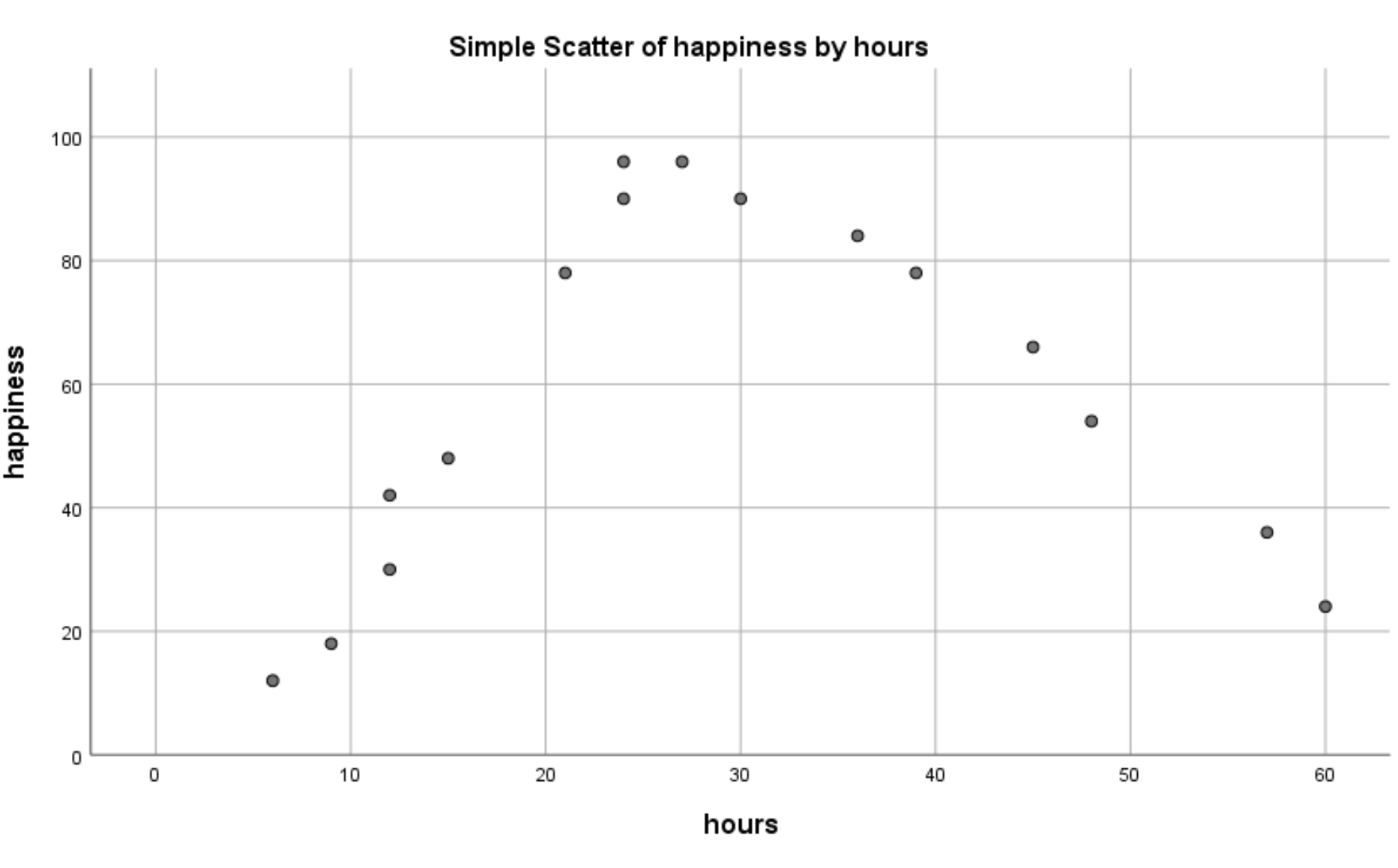
Мы ясно видим, что существует нелинейная связь между отработанным временем и счастьем. Это говорит нам о том, что квадратичная регрессия является подходящим методом для использования в этой ситуации.

Шаг 2: Создайте новую переменную.

Прежде чем мы сможем выполнить квадратичную регрессию, нам нужно создать переменную-предиктор для часов ² .

Перейдите на вкладку «Преобразование» , затем нажмите «Вычислить переменную» :

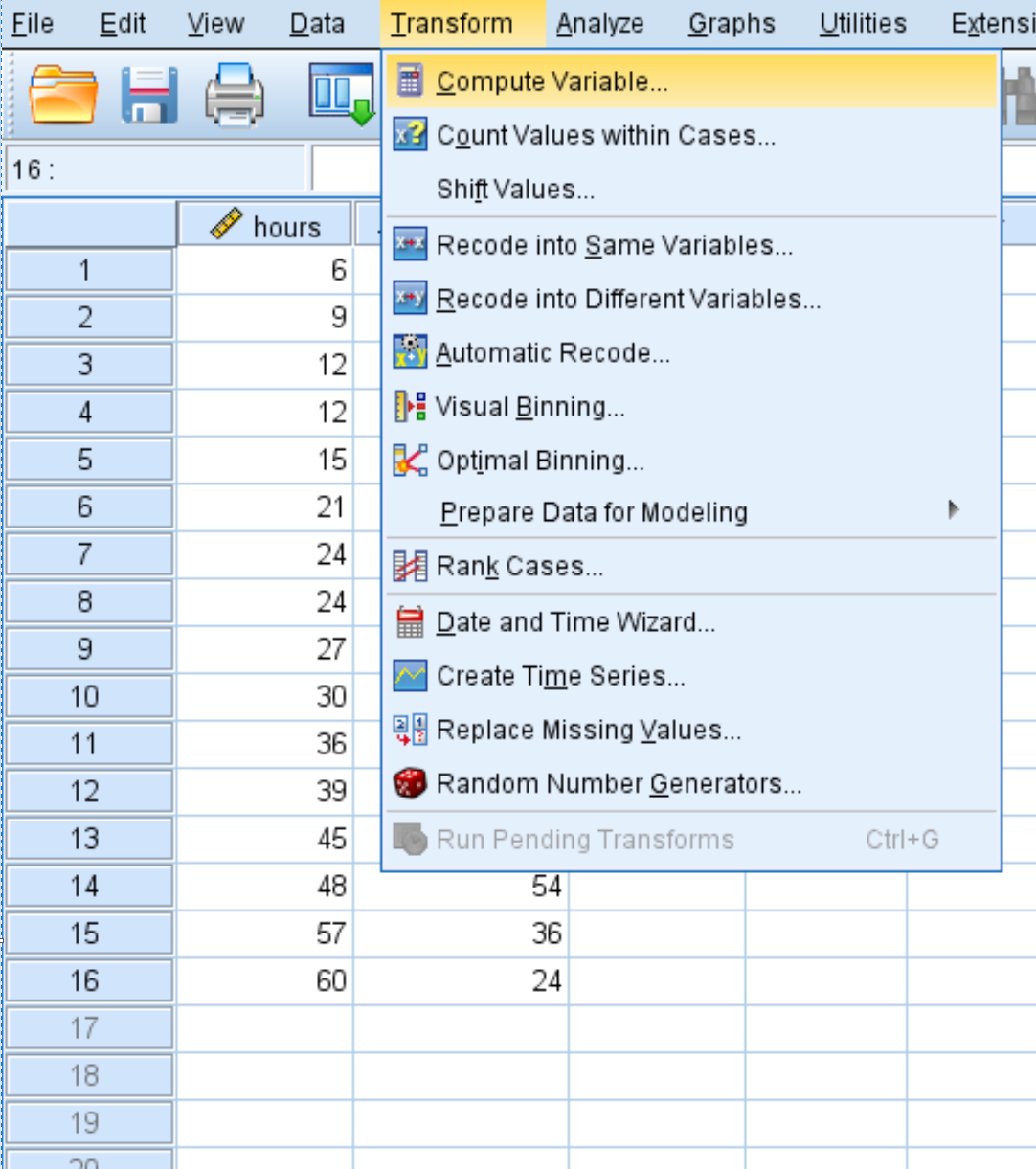
В появившемся новом окне назовите целевую переменную Часы2 и установите для нее значение Часы*часы :

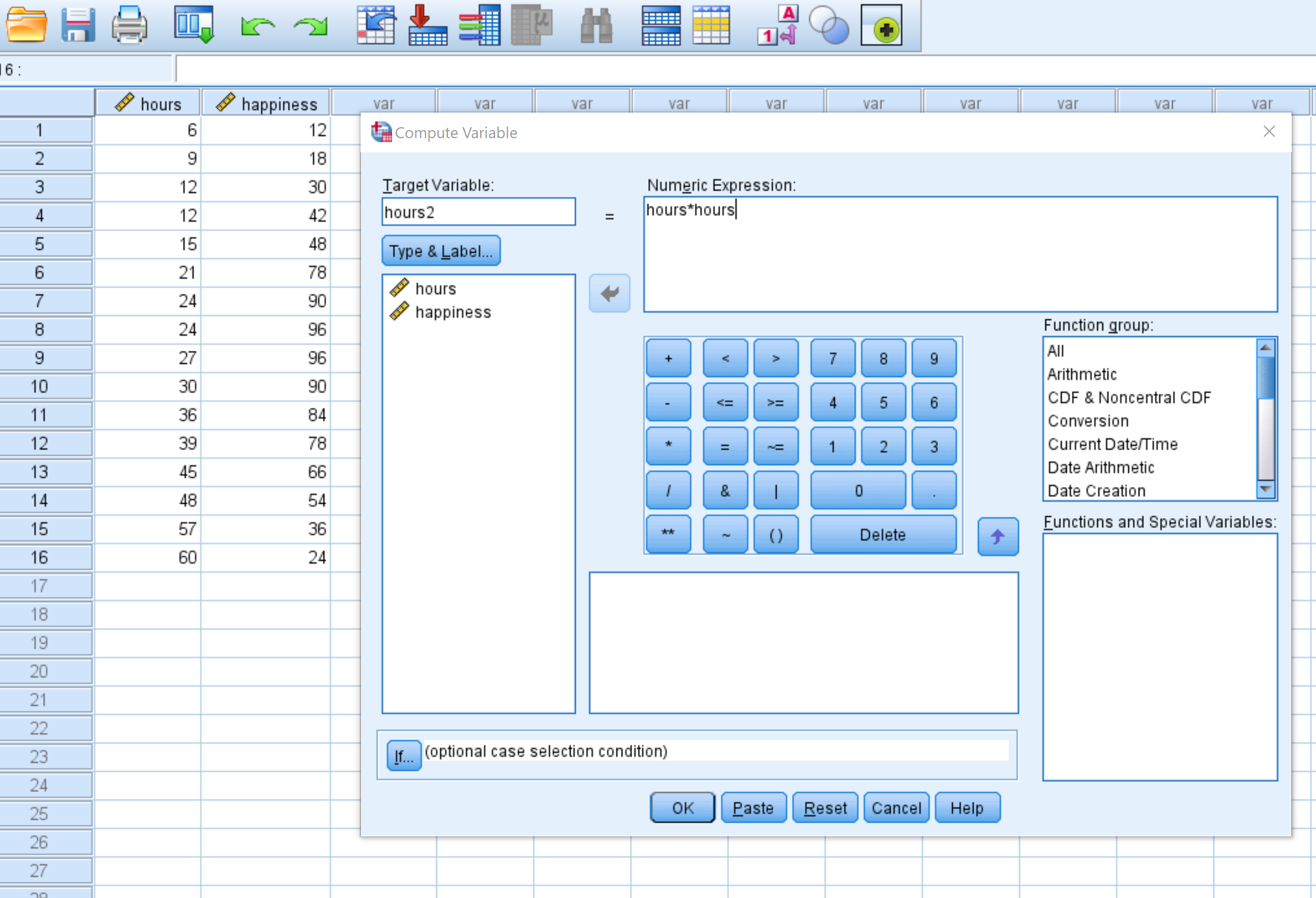
Как только вы нажмете «ОК» , переменная Часы2 появится в новом столбце:

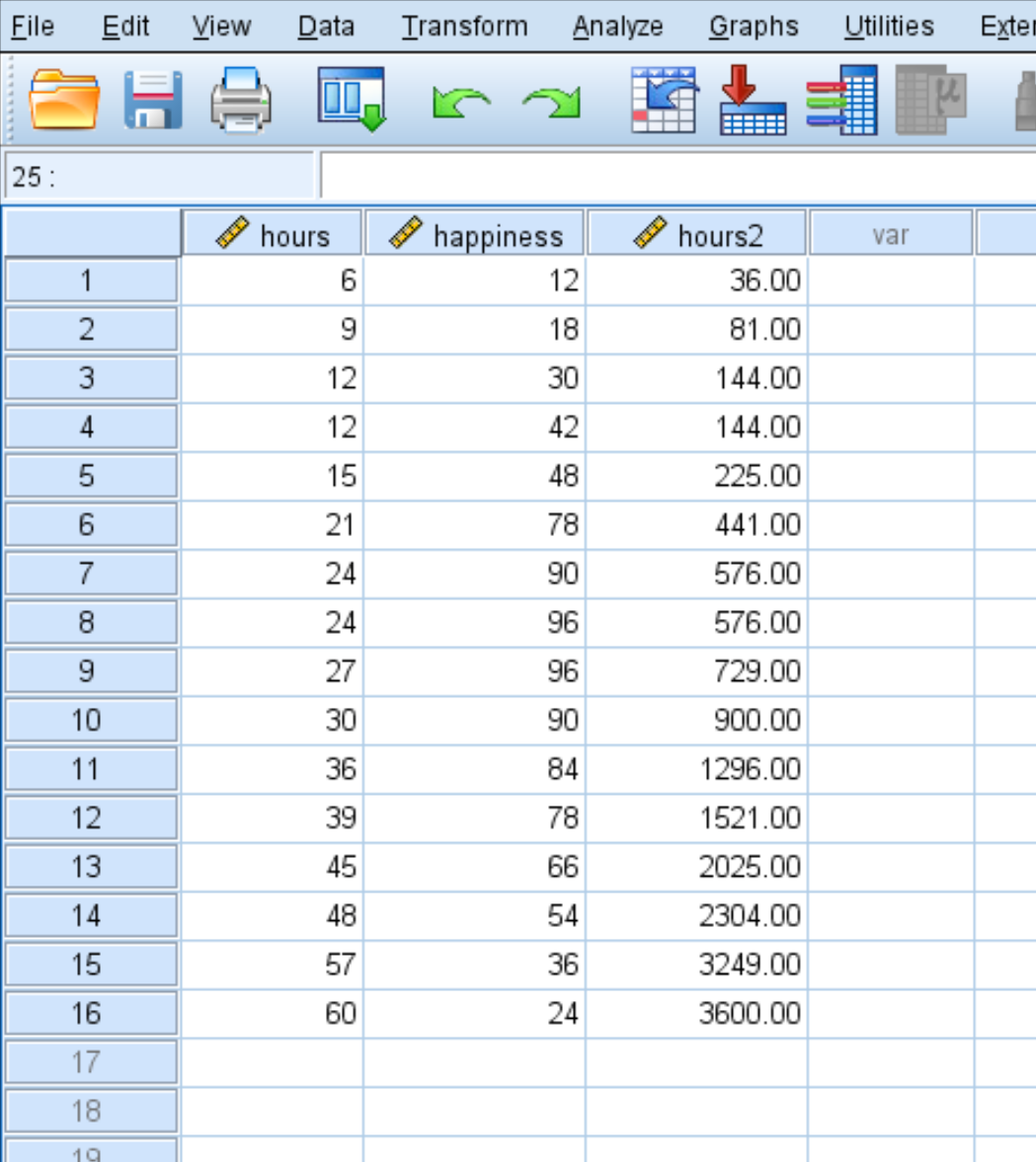
Шаг 3: Выполните квадратичную регрессию.

Далее мы выполним квадратичную регрессию. Перейдите на вкладку «Анализ» , затем «Регрессия» , затем «Линейная» :

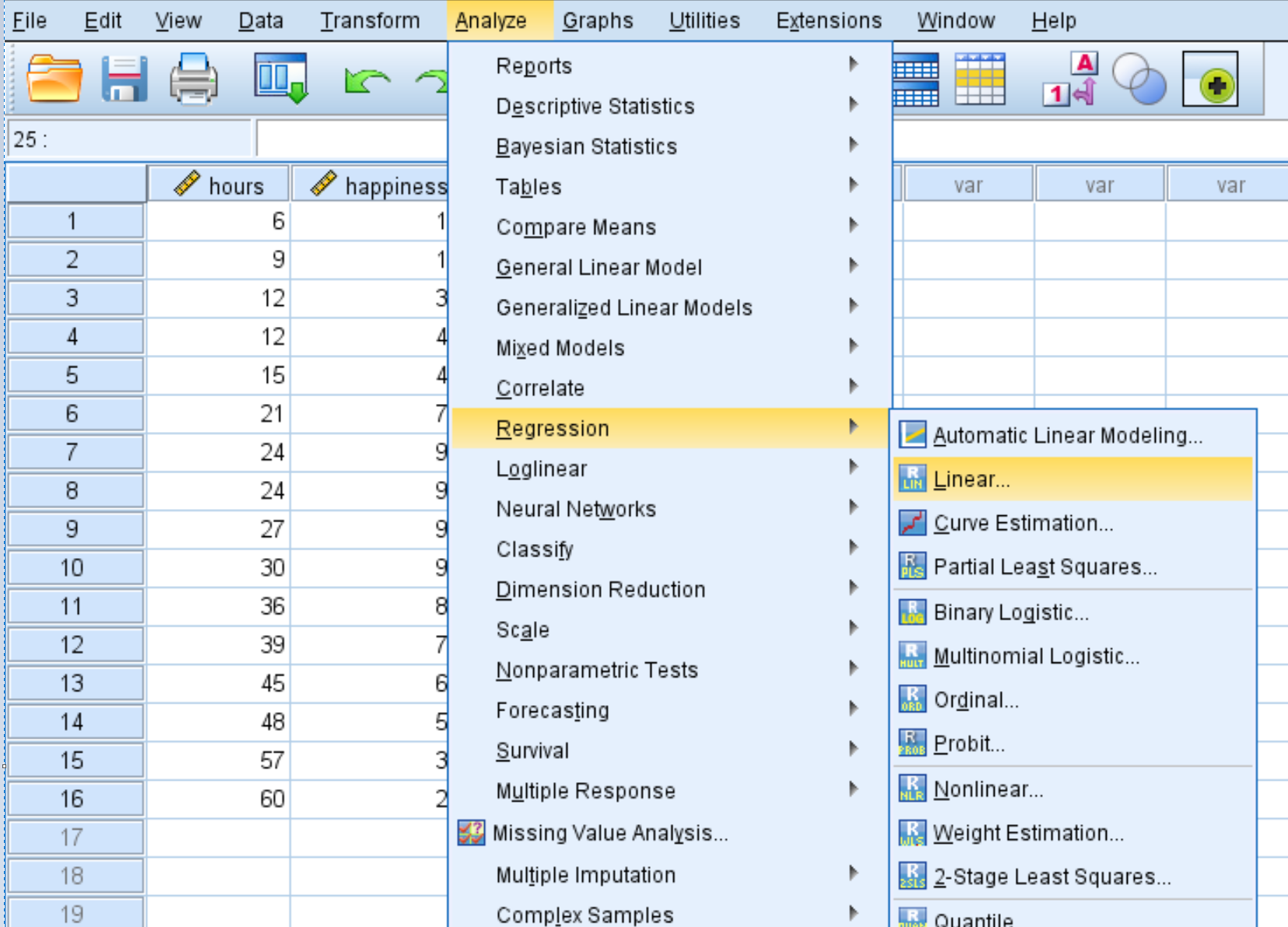
В появившемся новом окне перетащите счастье в поле «Зависимый». Перетащите Часы и Часы2 в поле «Независимые». Затем нажмите ОК .

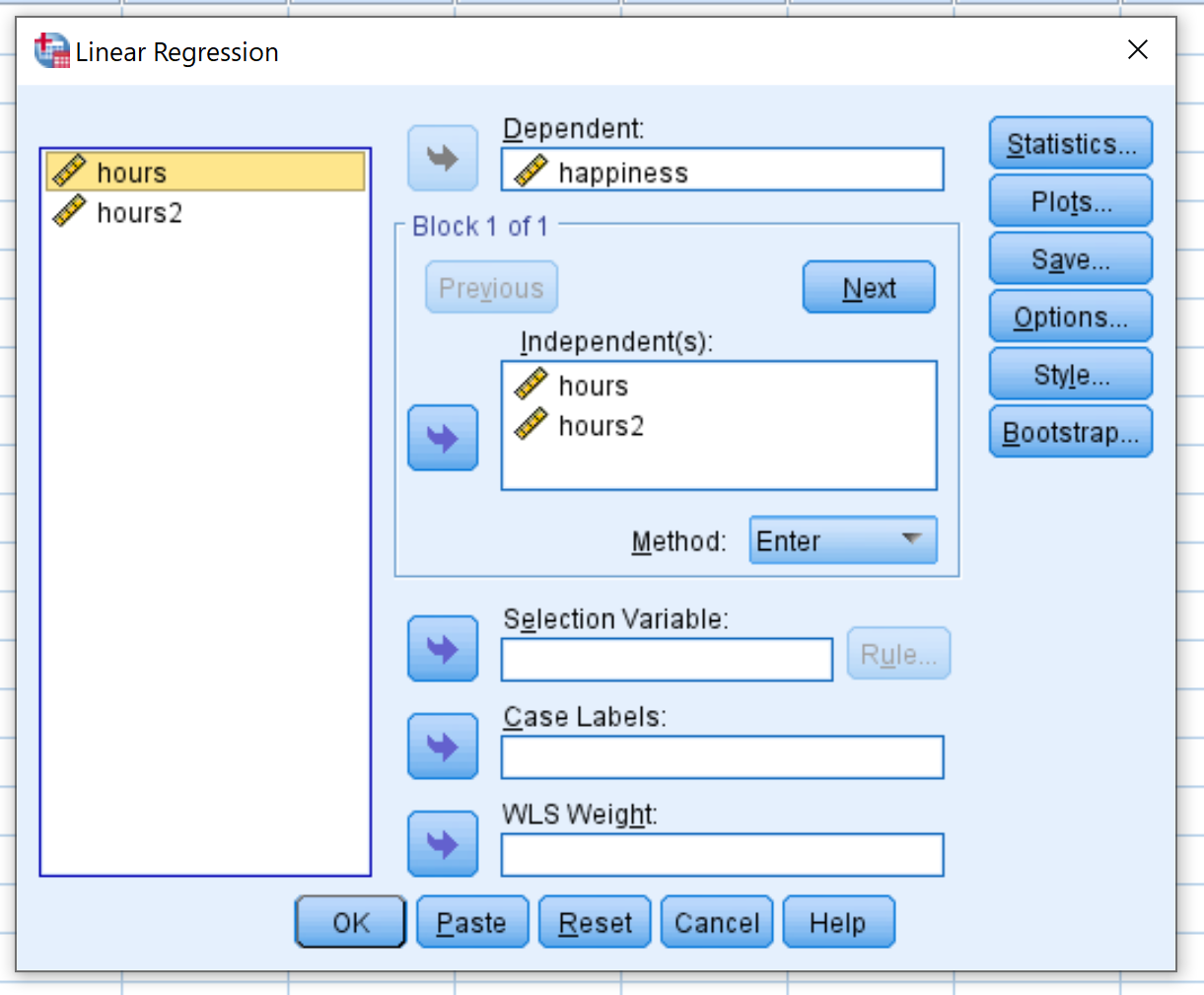
Шаг 4: Интерпретируйте результаты.

Как только вы нажмете «ОК» , результаты квадратичной регрессии появятся в новом окне.

Первая таблица, которая нас интересует, называется Model Summary :

Вот как интерпретировать наиболее важные цифры в этой таблице:

• R-квадрат: это доля дисперсии переменной ответа, которую можно объяснить объясняющими переменными. В этом примере 90,9% изменений счастья можно объяснить переменными часы и часы ² .
• Стандарт. Ошибка оценки: стандартная ошибка — это среднее расстояние между наблюдаемыми значениями и линией регрессии. В данном примере наблюдаемые значения отклоняются в среднем на 9519 единиц от линии регрессии.

Следующая таблица, которая нас интересует, называется ANOVA :

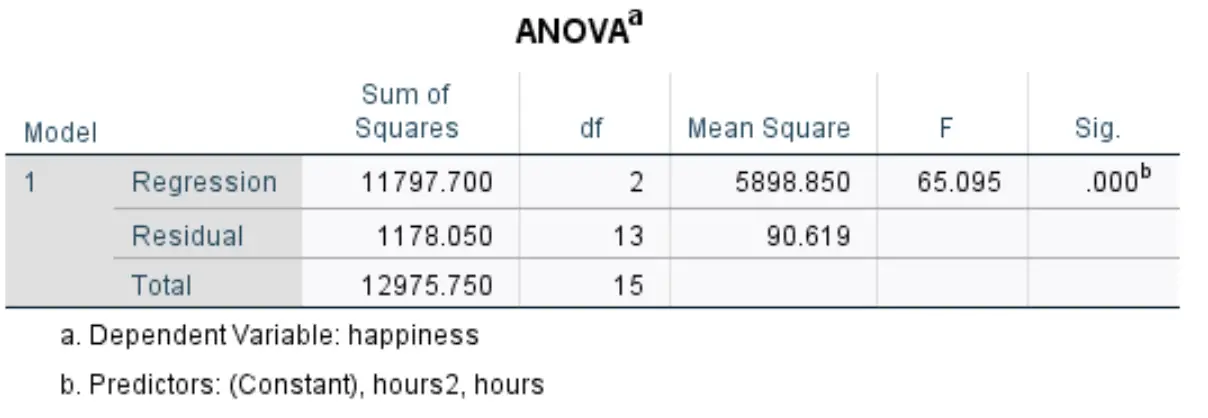
Вот как интерпретировать наиболее важные цифры в этой таблице:

• F: это общая статистика F для регрессионной модели, рассчитанная как среднеквадратическая регрессия / среднеквадратическая невязка.
• Sig: Это значение p, связанное с общей статистикой F. Это говорит нам, является ли регрессионная модель в целом статистически значимой или нет. В этом случае значение p равно 0,000, что указывает на то, что объясняющие переменные часы и часы ² вместе взятые имеют статистически значимую связь с результатом экзамена.

Следующая таблица, которая нас интересует, называется Коэффициенты :

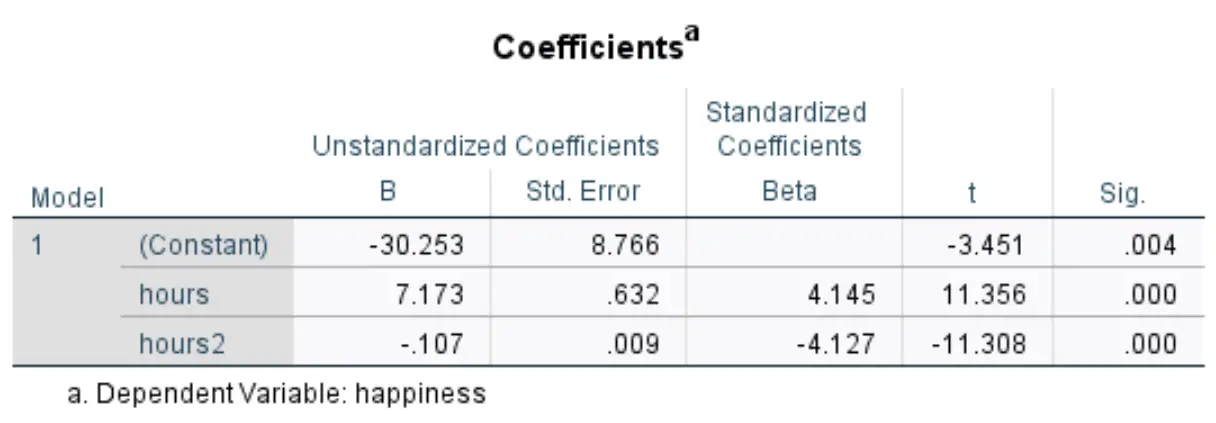
Мы можем использовать значения в столбце «Нестандартизированный B» , чтобы сформировать расчетное уравнение регрессии для этого набора данных:

Предполагаемый уровень счастья = -30,253 + 7,173*(часы) – 0,107*(часы ² )

Мы можем использовать это уравнение, чтобы определить предполагаемый уровень счастья человека на основе количества отработанных часов в неделю. Например, человек, который работает 60 часов в неделю, должен иметь уровень счастья 14,97:

Предполагаемый уровень счастья = -30,253 + 7,173*(60) – 0,107*(60 ² ) = 14,97 .

И наоборот, человек, который работает 30 часов в неделю, должен иметь уровень счастья 88,65:

Предполагаемый уровень счастья = -30,253 + 7,173*(30) – 0,107*(30 ² ) = 88,65 .

Шаг 5: Сообщите о результатах.

Наконец, мы хотим сообщить о результатах нашей квадратичной регрессии. Вот пример того, как это сделать:

Квадратичная регрессия была проведена для количественной оценки взаимосвязи между количеством часов, отработанных человеком, и соответствующим ему уровнем счастья (измеряется от 0 до 100). Для анализа была использована выборка из 16 человек.

Результаты показали, что существует статистически значимая связь между объясняющими переменными «часы» и «часы ^2» и переменной-ответом «счастье» (F(2, 13) = 65,095, p <0,000).

Вместе эти две объясняющие переменные объясняют 90,9% изменчивости счастья.

Уравнение регрессии оказалось таким:

Предполагаемый уровень счастья = -30,253 + 7,173 (часы) – 0,107 ( ² часа)