Как выполнить простую линейную регрессию в spss
Простая линейная регрессия — это метод, который мы можем использовать, чтобы понять взаимосвязь между переменной-предиктором и переменной ответа.
В этом руководстве объясняется, как выполнить простую линейную регрессию в SPSS.
Пример: простая линейная регрессия в SPSS
Допустим, у нас есть следующий набор данных, который показывает количество учебных часов и оценку на экзамене, полученную 20 студентами:
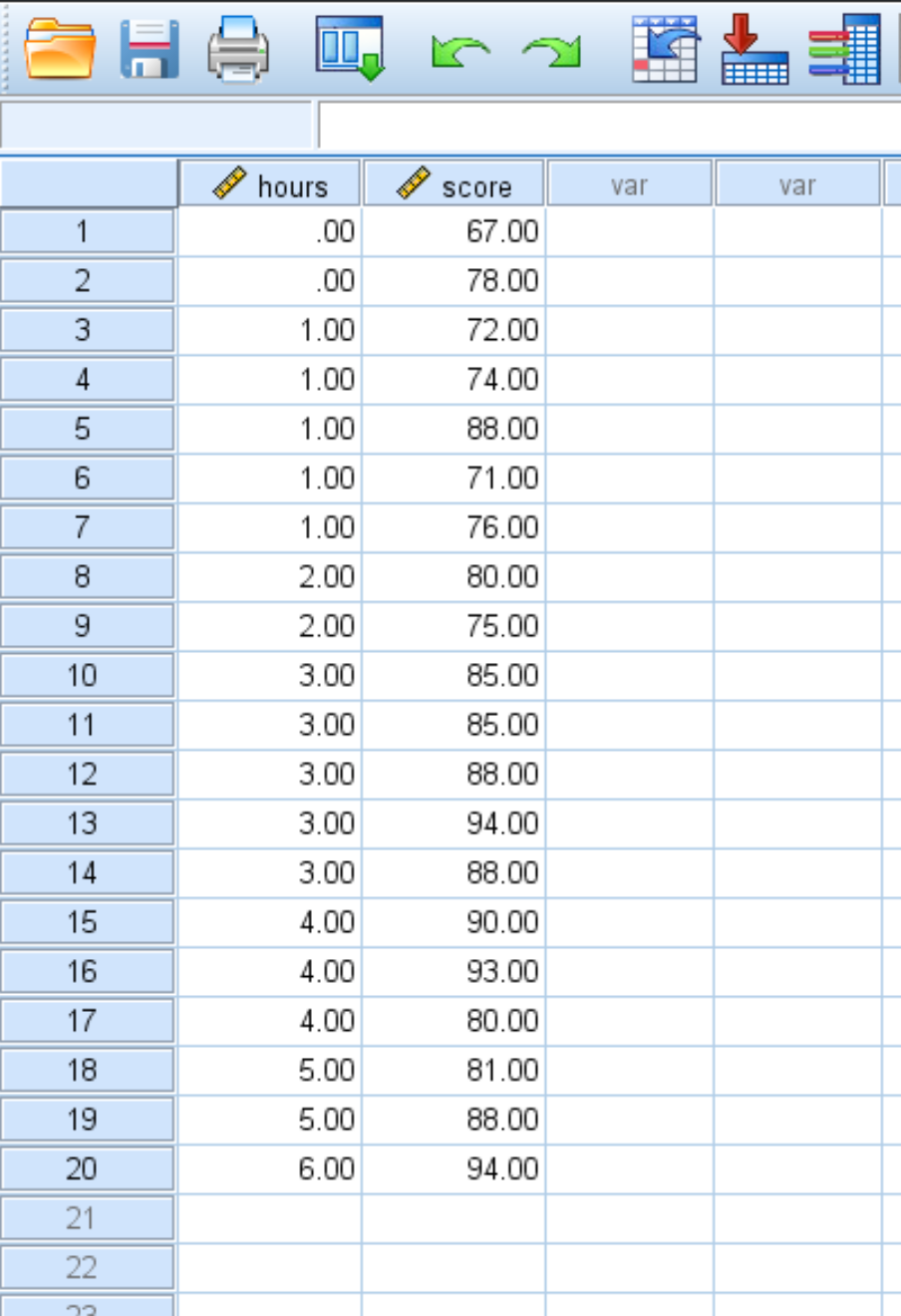
Используйте следующие шаги, чтобы выполнить простую линейную регрессию на этом наборе данных, чтобы количественно оценить взаимосвязь между учебными часами и баллами на экзамене:
Шаг 1: Визуализируйте данные.
Сначала мы создадим диаграмму рассеяния, чтобы визуализировать взаимосвязь между часами и баллами, чтобы гарантировать, что взаимосвязь между двумя переменными выглядит линейной. В противном случае простая линейная регрессия не будет подходящим методом.
Откройте вкладку «Диаграммы» , затем нажмите «Построитель диаграмм »:
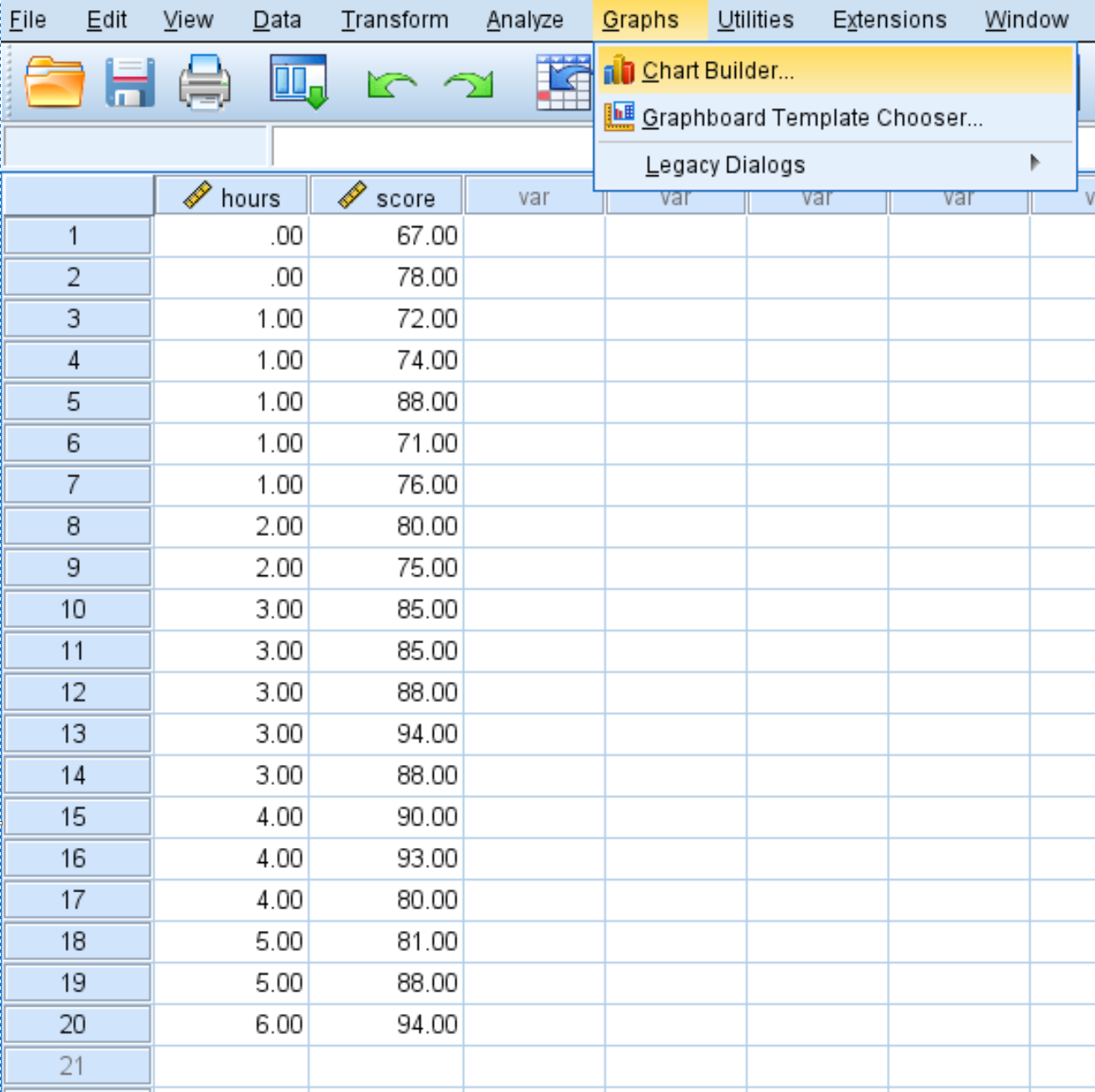
В меню «Выбрать из» щелкните и перетащите Scatter/Dot в главное окно редактирования. Затем перетащите переменное время на ось X, а результат — на ось Y.
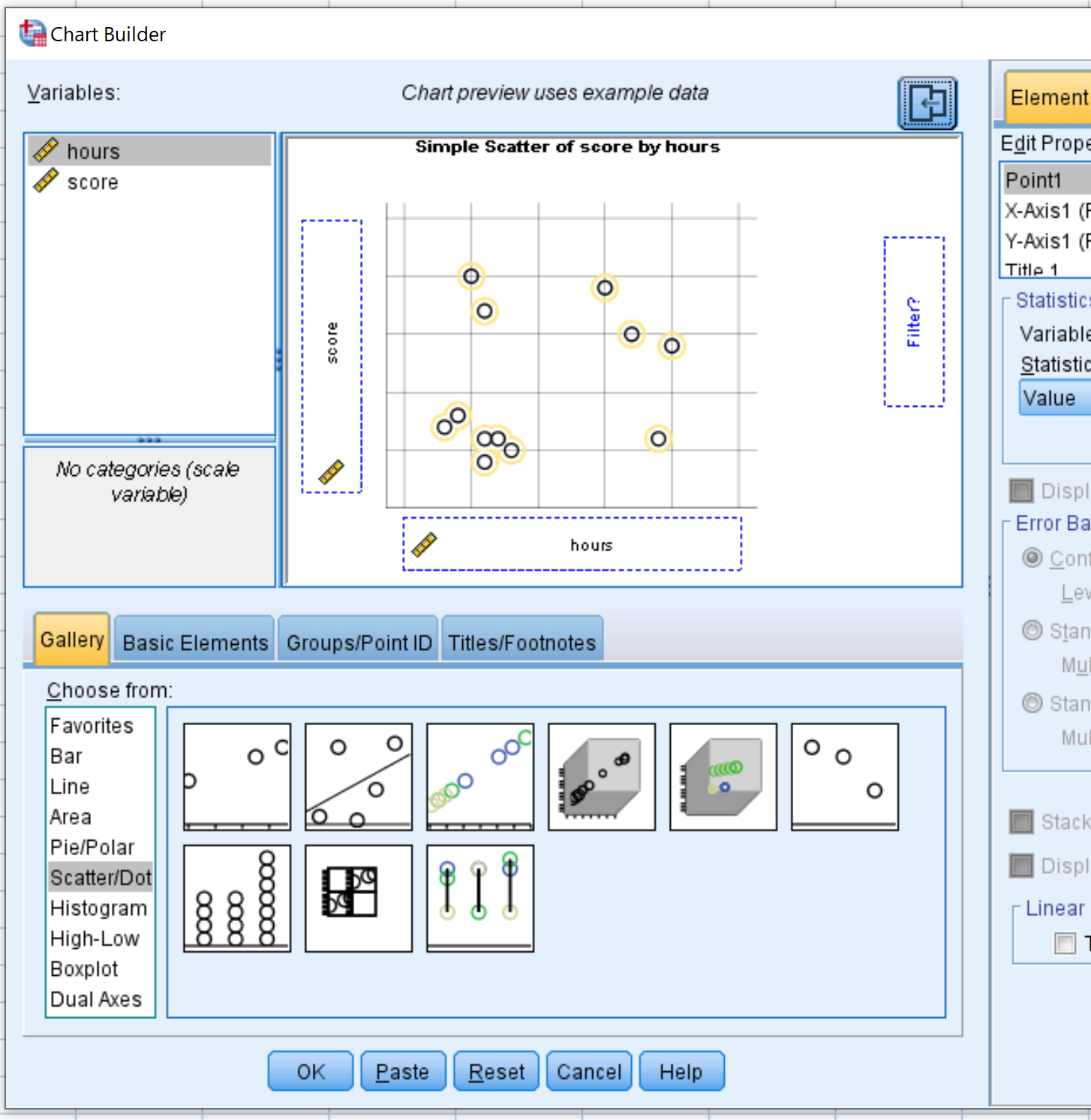
Как только вы нажмете «ОК» , появится следующая диаграмма рассеяния:
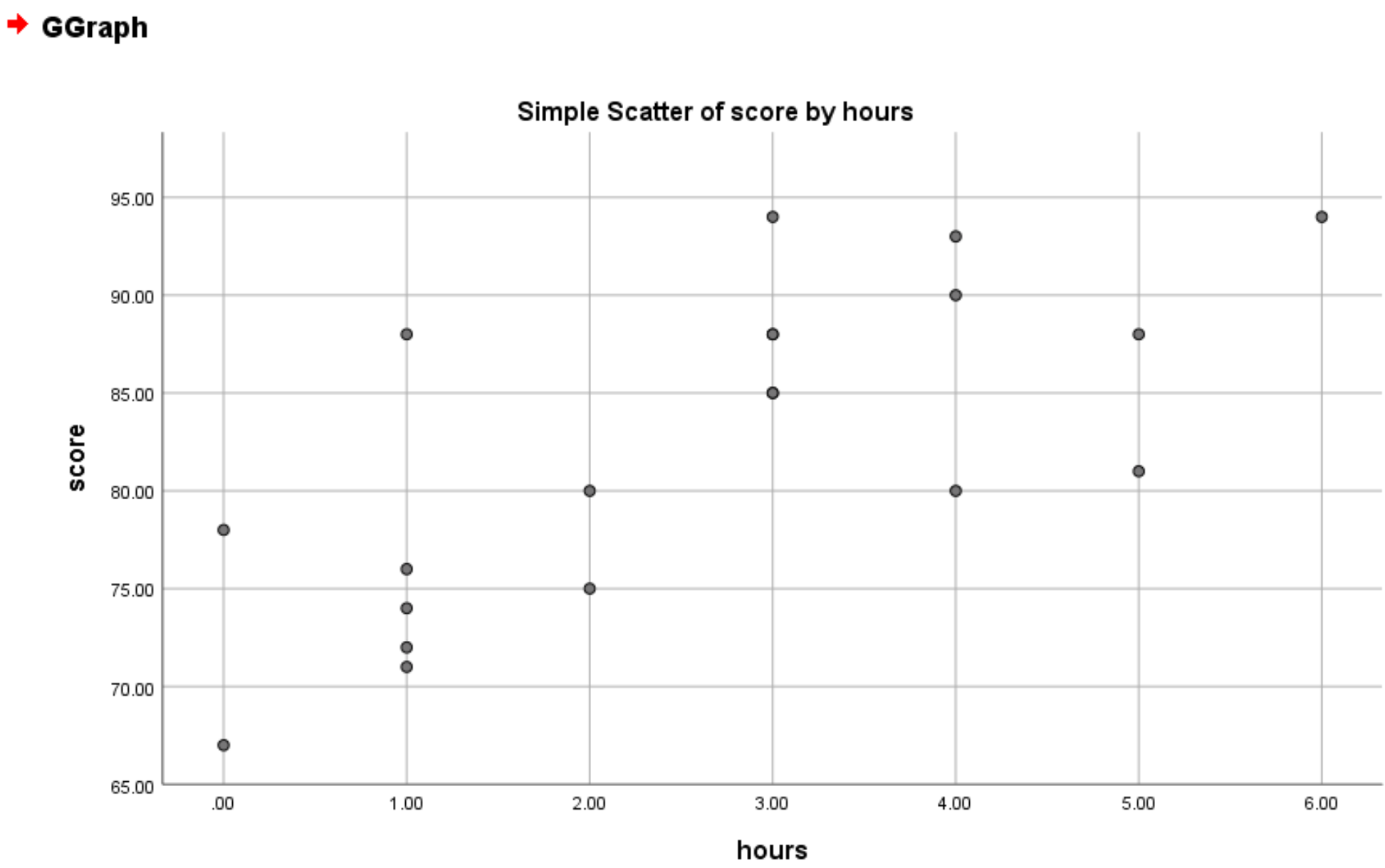
Из графика мы видим, что существует положительная линейная зависимость между часами и баллами. В целом, студенты, которые учатся больше часов, как правило, имеют более высокие баллы.
Поскольку между двумя переменными существует четкая линейная связь, мы продолжим подгонять простую модель линейной регрессии к набору данных.
Шаг 2. Подберите простую модель линейной регрессии.
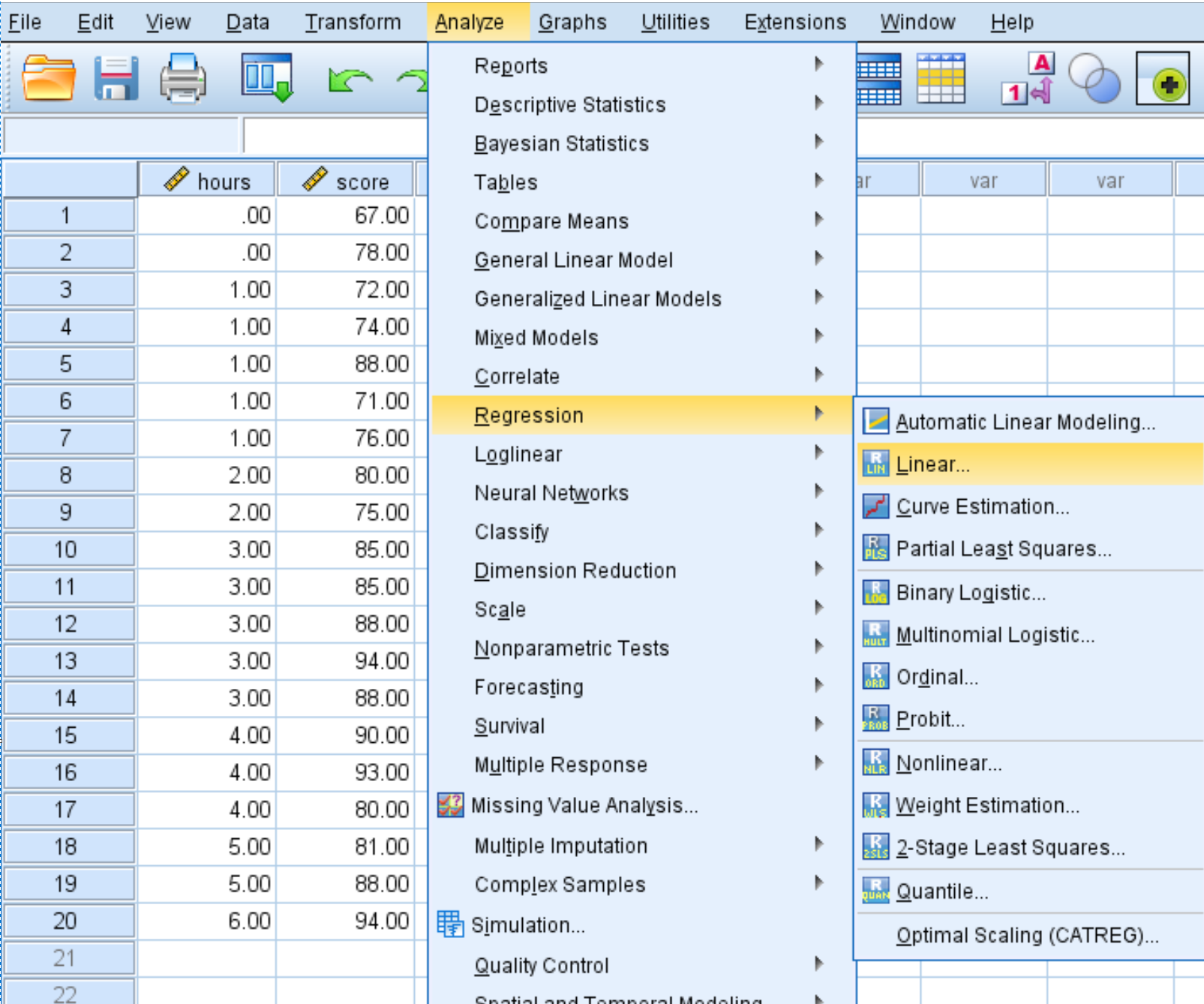
Перейдите на вкладку «Анализ» , затем «Регрессия» , затем «Линейная» :
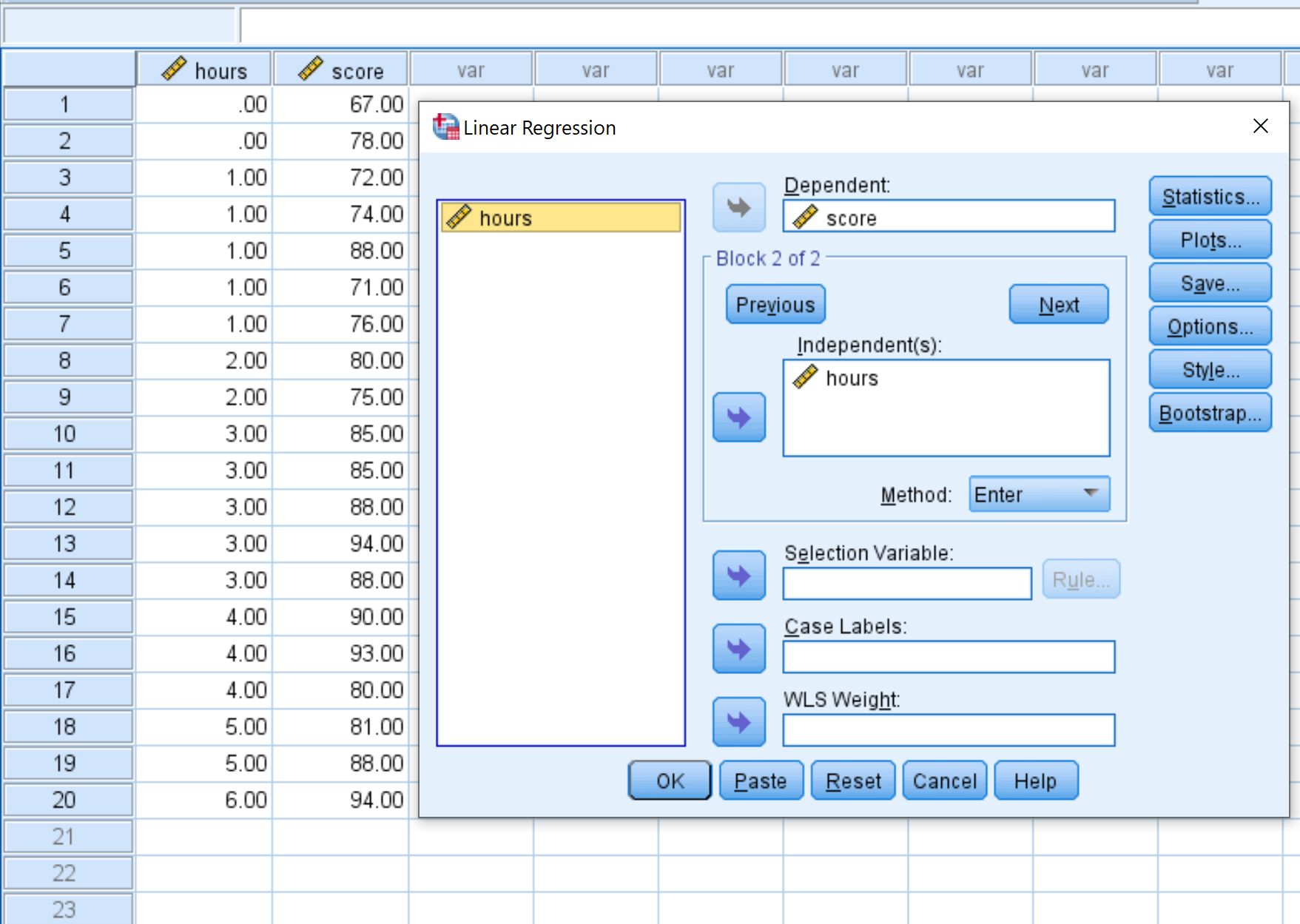
В появившемся новом окне перетащите переменную оценку в поле «Зависимый», а часы — в поле «Независимый». Затем нажмите ОК .
Шаг 3: Интерпретируйте результаты.
Как только вы нажмете «ОК» , появятся результаты простой линейной регрессии. Первая таблица, которая нас интересует, — это таблица под названием Model Summary :
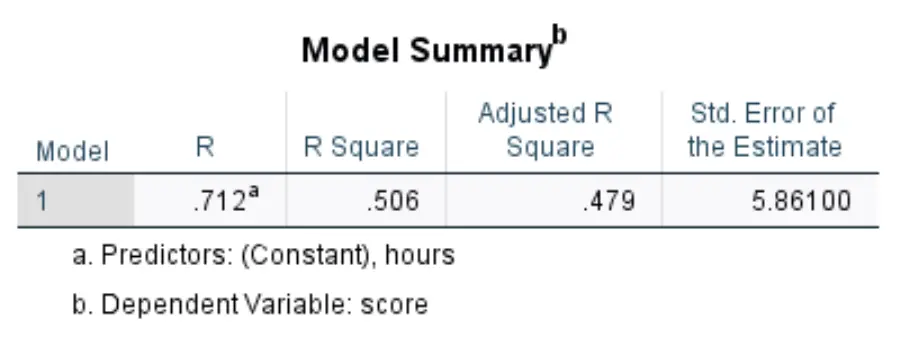
Вот как интерпретировать наиболее важные цифры в этой таблице:
- R-квадрат: это доля дисперсии переменной ответа, которую можно объяснить объясняющей переменной. В этом примере 50,6% различий в результатах экзамена можно объяснить количеством учебных часов.
- Стандарт. Ошибка оценки: стандартная ошибка — это среднее расстояние между наблюдаемыми значениями и линией регрессии. В данном примере наблюдаемые значения отклоняются в среднем на 5861 единицу от линии регрессии.
Следующая таблица, которая нас интересует, называется Коэффициенты :
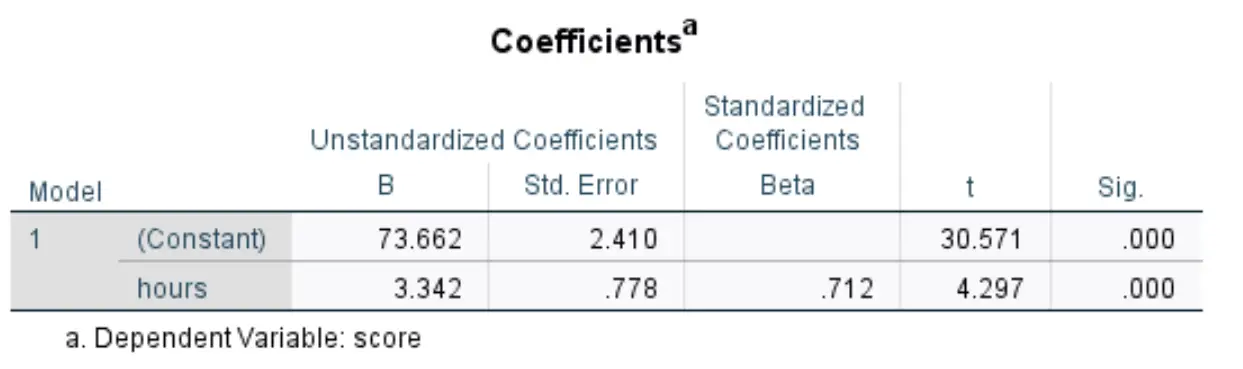
Вот как интерпретировать наиболее важные цифры в этой таблице:
- Нестандартизированный B (константа) : сообщает нам среднее значение переменной отклика , когда переменная-предиктор равна нулю. В этом примере средний балл экзамена составляет 73,662 , когда количество учебных часов равно нулю.
- B нестандартизированный (часы): это говорит нам о среднем изменении переменной ответа, связанном с увеличением на одну единицу предикторной переменной. В этом примере каждый дополнительный час обучения связан в среднем с увеличением балла на экзамене на 3342 балла.
- Sig (часы): это значение p , связанное со статистикой теста в течение часов. В этом случае, поскольку это значение меньше 0,05, мы можем заключить, что переменная-предиктор часы является статистически значимой.
Наконец, мы можем сформировать уравнение регрессии, используя значения констант и часов . В этом случае уравнение будет иметь вид:
Предполагаемый балл за экзамен = 73,662 + 3,342*(часы)
Мы можем использовать это уравнение, чтобы найти примерную оценку студента на экзамене на основе количества изученных часов.
Например, студент, который учится 3 часа, должен набрать на экзамене балл 83,688:
Предполагаемый балл на экзамене = 73,662 + 3,342*(3) = 83,688
Шаг 4: Сообщите о результатах.
Наконец, мы хотим подвести итоги нашей простой линейной регрессии. Вот пример того, как это сделать:
Для количественной оценки взаимосвязи между учебными часами и оценкой на экзамене была проведена простая линейная регрессия. Для анализа была использована выборка из 20 студентов.
Результаты показали, что существует статистически значимая связь между учебными часами и оценкой за экзамен (t = 4,297, p <0,000) и что изученные часы составляют 50,6% объясненной изменчивости оценок за экзамен. экзамен.
Уравнение регрессии оказалось таким:
Предполагаемый балл за экзамен = 73,662 + 3,342*(часы)
Каждый дополнительный час обучения связан в среднем с увеличением балла на экзамене на 3342 балла.
Дополнительные ресурсы
В следующих руководствах объясняется, как выполнять другие распространенные задачи в SPSS:
Как выполнить множественную линейную регрессию в SPSS
Как выполнить квадратичную регрессию в SPSS
Как выполнить логистическую регрессию в SPSS