Stdev.p и stdev.s в excel: в чем разница?
Для расчета стандартного отклонения в Excel можно использовать три различные функции:
1. STDEV.P: Эта функция рассчитывает стандартное отклонение генеральной совокупности. Используйте эту функцию, когда диапазон значений представляет всю совокупность.
Эта функция использует следующую формулу:
Стандартное отклонение совокупности = √Σ (x i – μ) 2 / N
Золото:
- Σ: греческий символ, означающий «сумма».
- x i : i-е значение набора данных
- μ: Среднее число населения
- N: Общее количество наблюдений
2. STDEV.S: Эта функция рассчитывает стандартное отклонение выборки. Используйте эту функцию, когда диапазон значений представляет собой выборку значений, а не всю совокупность.
Эта функция использует следующую формулу:
Стандартное отклонение выборки = √Σ (x i – x ) 2 / (n-1)
Золото:
- Σ: греческий символ, означающий «сумма».
- x i : i-е значение набора данных
- x : Образец означает
- N: Общее количество наблюдений
3. STDEV: Эта функция также рассчитывает стандартное отклонение выборки. Она вернет точно то же значение, что и функция STDEV.S .
Техническое примечание:
Поскольку формула стандартного отклонения генеральной совокупности делится на N вместо n-1 , стандартное отклонение генеральной совокупности всегда будет меньше стандартного отклонения выборки.
Причина, по которой стандартное отклонение генеральной совокупности будет меньше, заключается в том, что если мы знаем каждое значение генеральной совокупности, то мы знаем точное стандартное отклонение.
Однако, когда у нас есть только выборка населения, у нас больше неопределенности относительно точного стандартного отклонения всей совокупности, поэтому наша оценка стандартного отклонения должна быть больше.
В следующем примере показано, как использовать эти функции на практике.
Пример: STDEV.P против STDEV.S в Excel
Предположим, у нас есть следующий набор данных в Excel:
На следующем снимке экрана показано, как рассчитать стандартное отклонение набора данных с использованием трех различных формул стандартного отклонения:
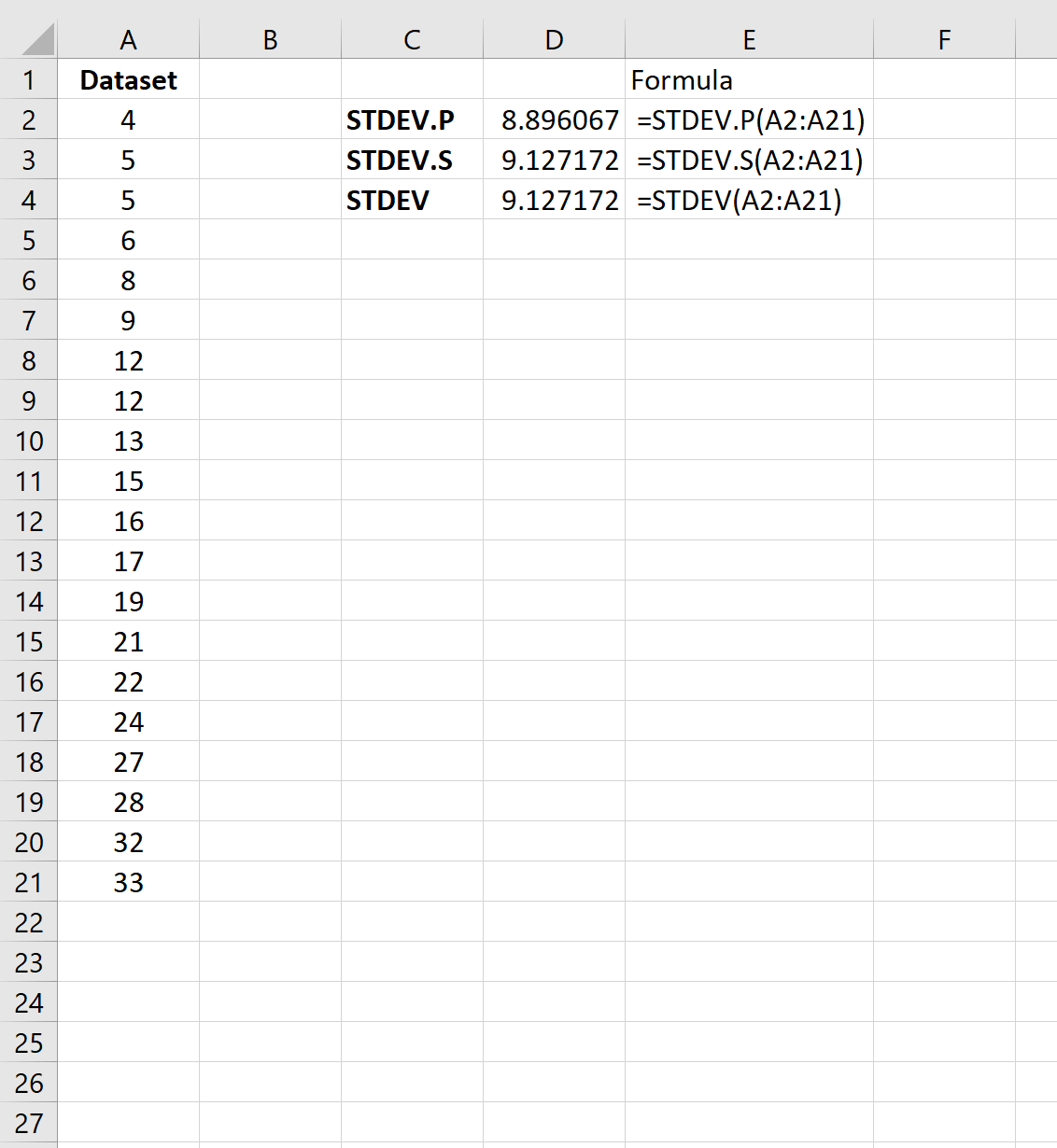
Стандартное отклонение выборки составляет 9,127 , а стандартное отклонение генеральной совокупности — 8,896 .
Как упоминалось ранее, стандартное отклонение генеральной совокупности всегда будет меньше стандартного отклонения выборки.
Когда использовать STDEV.P и STDEV.S
В большинстве случаев мы не можем собрать данные по всему населению. Поэтому мы собираем данные только для выборки населения.
Итак, мы почти всегда используем STDEV.S для расчета стандартного отклонения набора данных, поскольку наш набор данных обычно представляет собой выборку.
Обратите внимание, что STDEV и STDEV.S возвращают одни и те же значения, поэтому мы можем использовать любую функцию для расчета выборочного стандартного отклонения данного набора данных.