Как выполнить корреляционный t-тест
Коэффициент корреляции Пирсона используется для количественной оценки линейной связи между двумя переменными.
Он всегда принимает значение от -1 до 1, где:
- -1 указывает на совершенно отрицательную линейную корреляцию.
- 0 указывает на отсутствие линейной корреляции.
- 1 указывает на совершенно положительную линейную корреляцию.
Чтобы определить, является ли коэффициент корреляции статистически значимым, вы можете выполнить t-критерий, который включает в себя расчет t-показателя и соответствующего значения p.
Формула для расчета t-показателя выглядит следующим образом:
т = r√ (n-2) / (1-r 2 )
Золото:
- r: коэффициент корреляции
- n: Размер выборки
Значение p рассчитывается как соответствующее двустороннее значение p для t-распределения с n-2 степенями свободы.
В следующем примере показано, как выполнить t-тест для коэффициента корреляции.
Пример: выполнение t-теста для корреляции
Предположим, у нас есть следующий набор данных с двумя переменными:
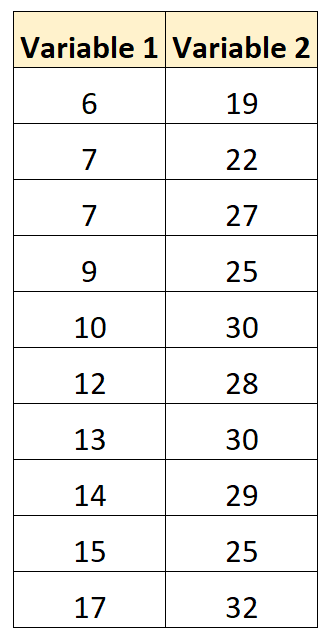
Используя некоторое статистическое программное обеспечение (Excel, R, Python и т. д.), мы можем рассчитать коэффициент корреляции между двумя переменными, равный 0,707 .
Это очень положительная корреляция, но чтобы определить, является ли она статистически значимой, нам необходимо рассчитать соответствующие t-показатель и p-значение.
Мы можем рассчитать t-показатель следующим образом:
- т = r√ (n-2) / (1-r 2 )
- t = 0,707√ (10-2) / (1-0,707 2 )
- т = 2,828
Используя калькулятор T-показателя P-значения , мы находим, что соответствующее значение p равно 0,022 .
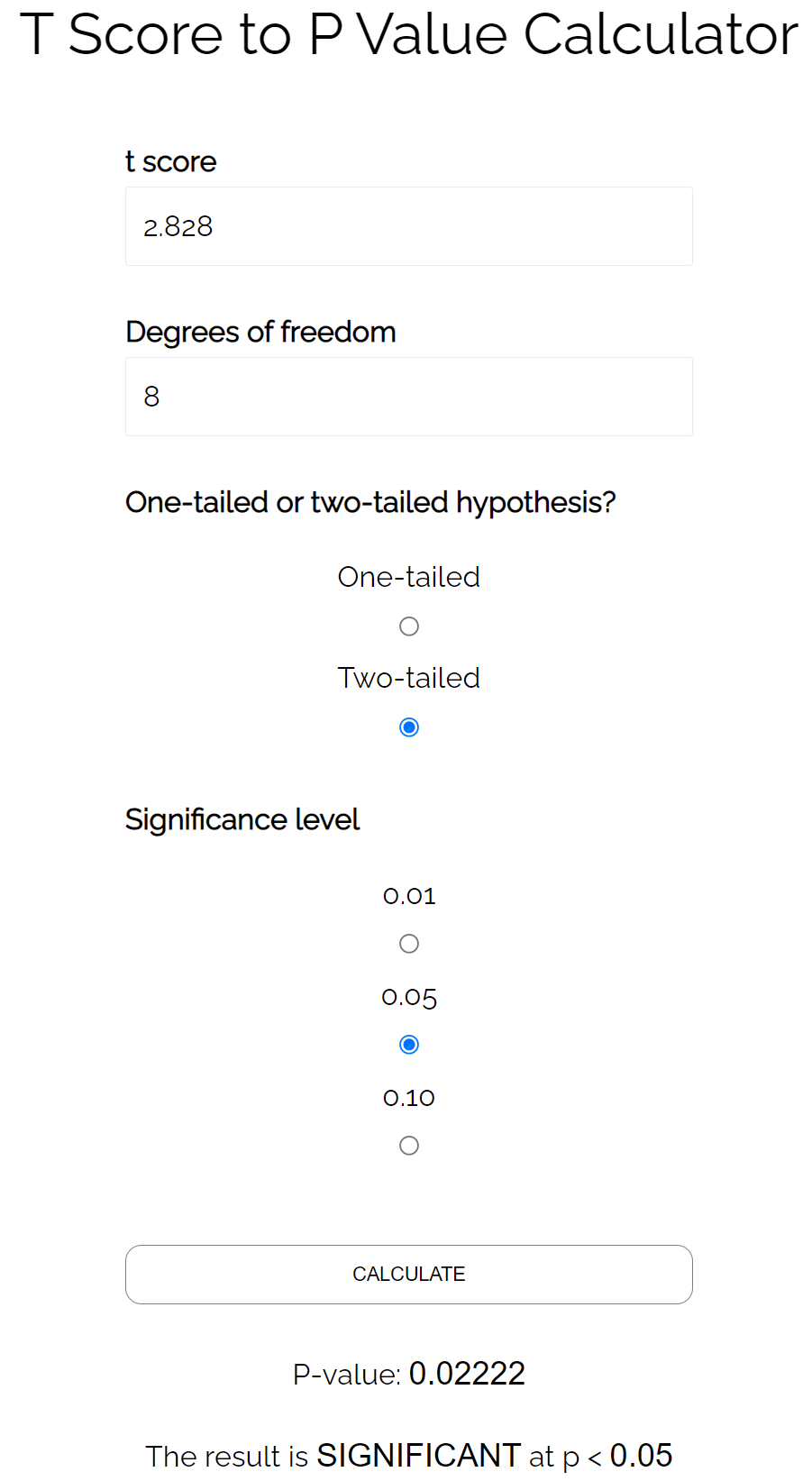
Поскольку это значение p меньше 0,05, мы можем сделать вывод, что корреляция между этими двумя переменными статистически значима.
Дополнительные ресурсы
Как выполнить корреляционный тест в Excel
Как выполнить корреляционный тест в R
Что считается «слабой» корреляцией?
Что считается «сильной» корреляцией?